Youmath Solido di rotazione Andreaminini Geometria Solidi di rotazione Salesianibra Solidi di rotazione pdf Latteseditori Geometria solida pdf Math Solidi di rotazione Sapere.virgilio Solidi di rotazione cosa sono Mathtube.altervista Solidi di rotazione Matematicaoggi Esercizi sul cilindro pdf Library.weschool Solidi di rotazione formule Sfera Cono Cilindro volume superficie Hubscuola Solidi di rotazione superficie e volume del cilindro del cono e della sfera Impariamoinsieme Solidi di rotazione Tecnologiaduepuntozero Sviluppo dei solidi Esercizi.zanichelli Solidi di rotazione Ubimath Geometria 3d Eduboom Solidi di rotazione cono cilindro sfera Skuola.net Solidi di rotazione Amicamat Geometria nello spazio Solidi di rotazione Schooltoon I solidi di rotazione Geogebra Scuolaelettrica Risolti solidi di rotazione Valeriavecchi Solidi di rotazione pdf Vivalascuola.studenti Solidi di rotazione Web.tiscali Solidi di rotazione pdf
![]()
Con la rotazione di molti poligoni semplici attorno ai loro lati si ottengono svariati solidi
Tabella riassuntiva dei solidi di rotazione
Tabella riassuntiva dei solidi di rotazione 1
![]()
![]()
Ripasso di matematica Geometria dello spazio
Prisma retto Cilindro Superficie e Volume
Aritmetica Geometria Informatica
Geometria piana e solida
Elementi Fondamentali della Geometria
Geometria Solida Nozioni Generali
Yahoo! Video Solidi di Rotazione YouTube
![]()
![]()
GEOMETRIA SOLIDA - SOLIDI DI ROTAZIONE
SUPERFICI DI ROTAZIONE
Fate questo semplice esperimento.
Prendete un robusto filo di cotone e legate a un'estremità un peso:
ad esempio una piccola pietra o un dado metallico.
Tenendo in mano l'altra estremità del filo, imprimete un movimento rotatorio alla mano finché il peso non avrà raggiunto una certa velocità:
a questo punto avrete la sensazione visiva che il peso si muova lungo la base di una superficie conica.
Tale superficie è una superficie di rotazione, il cui asse è rappresentato dal filo verticale fermo, infatti ogni punto del filo (B, C, D) ruota descrivendo circonferenze i cui centri O', O'', O''' giacciono tutti sulla retta AA' che si chiama appunto asse di rotazione.
Diciamo che qui il filo in movimento ha generato una superficie di rotazione.
Allo stesso modo possiamo dire che la lama di un tornio da falegname imprime il suo profilo sul massello di legno messo in rotazione da un mandrino, funzionando quindi da generatrice.
Vogliamo precisare subito che:
Una superficie di rotazione generata da una linea curva non è sviluppabile su un piano.
Il filo in movimento dell'esperimento descritto e la curva BB' si dicono generatrici.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
SOLIDI DI ROTAZIONE
Se al posto di una linea facciamo ruotare un poligono (o qualsiasi linea piana chiusa) attorno ad una retta ad esso complanare, otteniamo un solido di rotazione.Ad esempio il triangolo rettangolo ABC che ruota attorno al cateto AC (fig. 331) genera un cono.
Alcuni dei solidi già incontrati nei capitoli precedenti possono essere ottenuti per rotazione di figure piane:
un rettangolo che ruota attorno ad un proprio lato genera un cilindro circolare retto (fig. 332 e 333);
un triangolo rettangolo che ruota attorno a un cateto genera un cono circolare retto;
un trapezio che ruota attorno all'altezza genera un tronco di cono circolare retto.
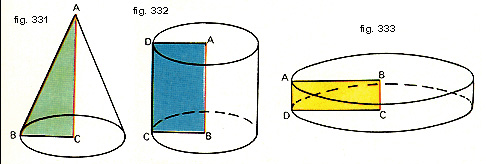
Con la rotazione di molti poligoni semplici attorno ai loro lati si ottengono svariati solidi.
Così per esempio un triangolo acutangolo che ruota attorno a un lato genera un doppio cono con un'unica base, mentre gli altri due lati fanno da apotema e l'altezza relativa al lato adottato come perno di rotazione corrisponde al raggio di base.
Un trapezio rettangolo che ruota attorno alla base maggiore forma un solido costituito da un cilindro sormontato da un cono aventi la base in comune;
l'apotema del cono è il lato obliquo, l'altezza è la differenza fra le basi del trapezio, l'altezza del cilindro è uguale alla base minore e l'altezza del trapezio diventa il raggio della base del solido.
Molti solidi di rotazione che incontriamo nella pratica quotidiana si ottengono per rotazione di figure piane attorno a un asse esterno;
essi hanno tutti forma anulare, sono cioè vuoi all'interno.
Pensiamo a un tubo di ferro:
è un solido di rotazione generato da un rettangolo che ruota attorno a una retta parallela a un lato;
lo chiameremo cilindro cavo.
Anche la ciambella di salvataggio è un solido di rotazione generato da un cerchio rotante attorno a una retta esterna.
Tale solido si chiama toro, e torica o toroidale Ia sua superficie.
La distanza OH, dal centro del cerchio all'asse di rotazione, è il raggio del toro.
Video:
SEZIONI
Chiamiamo sezione normale la figura piana che si ottiene tagliando un solido di rotazione con un piano perpendicolare al suo asse.La sezione normale di un solido di rotazione pieno è sempre un cerchio (fig. 341);
quella di un solido di rotazione cavo è sempre una corona circolare (fig. 342).
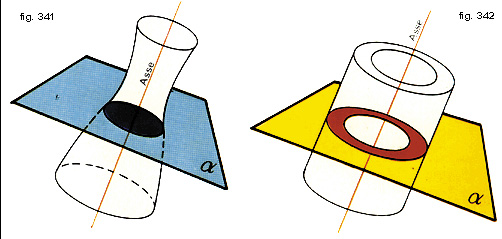
Chiamiamo sezione longitudinale la figura piana che si ottiene tagliando un solido di rotazione con un piano che contiene il suo asse.
Una sezione longitudinale mette bene in evidenza la figura piana che ha generato il solido.
VERO O FALSO?
1) La generatrice di una superficie di rotazione sviluppabile non può essere una linea curva.2) Alcuni poligoni generano solidi di rotazione la cui superficie non è sviluppabile.
3) La superficie toroidale delimita un solido cavo.
4) La sezione longitudinale di un solido di rotazione è sempre un cerchio.
5) La sezione normale di un tubo è una corona circolare.
1) Vero.
2) Falso: tutti i solidi di rotazione generati da poligoni sono sviluppabili, perché un poligono è costituito da segmenti di linea retta.
3) Vero.
4) Falso: la sezione longitudinale di un solido di rotazione corrisponde alla figura che lo genera.
5) Vero.
ESERCIZI
1) Determinare l'apotema di un cono circolare retto alto m 4 il cui volume misura mc 37,68.Troviamo dapprima il raggio con la prima delle (9) inverse:
+---------
¦ 3*37,68
r=m¦ ------- =m 3
\¦ 3,14*4
Ora applichiamo la (5):
+------
a=m\¦3²+ 4²=m 5
2) Un tubo di ferro lungo 50 cm ha lo spessore di mm 2 e il raggio interno di mm
11.Calcolare il suo peso, assumendo come peso specifico 7,8.
Troviamo innanzitutto il raggio esterno, che corrisponde alla somma del raggio interno e dello spessore:
R = mm (11+2) = mm 13
Ora possiamo calcolare il volume con la (19), ricordando che cm 50 = mm 500:
V = mm3 [3,14*500 (132-112)] = mm3 75.360
Infine il peso:
P = mg (75.360*7,8) = mg 587.808
3) Determinare la superficie di un doppio cono convesso il cui raggio di base misura m 6 e le due altezze m 8 e m 4,5.
Calcolate i due apotemi con le (20) e (21):
+------
a'=m\¦6²+ 8²=m 10
+--------
a"=m\¦6²+ 4,5²=m 7,5
Ora applichiamo la (23):S=m2[3,l4*6(10+7,5)]=
= m2 329,7
4) Determinare il peso di un anello d'oro del diametro di mm 16, di sezione circolare con raggio mm 0,5, assumendo il peso specifico dell'oro pari a 19,5.
Si tratta di un toro in cui R assume il valore di mm ( 16:2) = 8; con la (31) possiamo calcolare il volume:
V=mm3(2*3,142*8*0,52)=
= mm3 39,48
Ora troviamo il peso:
P = mg (39,48*19,5) = mg 769,8
Ed ecco, al solito, un problema concreto.
Vogliamo rifornire la nostra cantina con circa 500 bottiglie di «Chianti» da acquistare presso un'azienda di produzione vinicola.
Il vino viene fornito esclusivamente in damigiane.
Sapendo che ogni bottiglia contiene litri 0,75, si chiede quante damigiane dovranno essere acquistate.
Si vuol inoltre determinare il costo al litro, sapendo che ogni damigiana costa Euro. 200.
Determiniamo dapprima la capacità di ogni damigiana:
essa è formata da due tronchi di cono sovrapposti aventi una base in comune, precisamente quella il cui raggio misura cm 30; le altre basi hanno il raggio di cm 4 e cm 25.
Le due altezze misurano cm 15 e cm 35. Utilizzando la (15) otteniamo rapidamente il volume della damigiana.
Tronco di cono superiore:
V = cm3 [(3,14*15):3 (42+4*30+302)] = cm3 16.265,2
Tronco di cono inferiore:
V = cm3 [(3,14*35):3 (252+25*30+302)] = cm3 83.340,8
Il volume totale sarà dato dalla somma:
V = cm3 (16.265,2+83.340,8) = cm3 99.606
corrispondenti a litri 99,606.
La quantità di vino da acquistare è data da:
litri (0,75*500) = litri 375
che richiedono per il trasporto un numero di damigiane pari a:
(375:99,606) = 3,76
Per maggiore comodità ne acquisteremo quattro. Il prezzo del vino al litro sarà dato da:
Euro (200:99,606) = Euro 2,0079
Tabella riassuntiva dei solidi di rotazione (1ª)
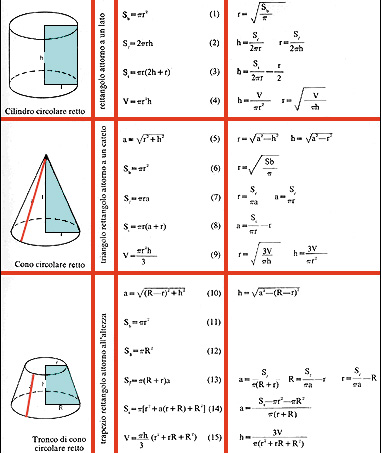
Tabella riassuntiva dei solidi di rotazione (2ª)
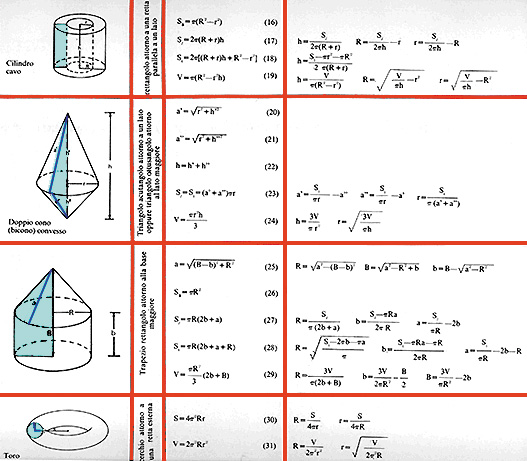
Vocabolario I F GB D e Vocabolario di Latino
àrido.
1 (agg.), secco. 2 fig. sentimentalmente povero. 3 -ménte (avv.) in modo arido. 4 (s.m. pl.), solidi misurabili come i liquidi.Inglese
dryFrancese
arideTedesco
dürrcoesione.
(s.f.), la forza che unisce le molecole di un corpo; massima nei solidi, media nei liquidi e minima nei gas.Inglese
cohesionFrancese
(f.) cohésionTedesco
(m.) Zusammenhaltestrattore.
(s.m.), 1 che è addetto a lavori di estrazione. 2 nelle armi da fuoco dispositivo per estrarre i bossoli dalla canna. 3 strumento chirurgico che serve ad estrarre corpi estranei agli organi. 4 in mecc. apparecchio per estrarre da una pressa un pezzo lavorato. 5 in chim. apparecchio di estrazione di solidi e liquidi.Inglese
extractorFrancese
(m.) extracteurTedesco
(m.) Auswerferfornello.
(s.m.), 1 apparecchio alimentato sia da combustibili solidi che liquidi o gassosi, serve per cuocere le vivande: - a gas. 2 cavità della pipa dove brucia il tabacco. 3 luogo delle caldaie dove avviene la combustione. 4 condotto di comunicazione fra due livelli di una miniera.Inglese
stoveFrancese
(m.) fourneauTedesco
(m.) kleiner Ofenfrantoio.
(s.m.), 1 macchina che serve a macinare o frantumare materiali solidi e compatti come rocce, olive, semi, ecc. 2 luogo ove si effettua la frangitura.Inglese
oil-millFrancese
(m.) broyeurTedesco
(f.) pressegeometrìa.
(s.f.), scienza che studia la proprietà delle figure piane e dei solidi.Inglese
geometryFrancese
(f.) géométrieTedesco
(f.) Geometriegeostàtica.
(s.f.), parte della fisica che studia l'equilibrio dei corpi solidi.Inglese
geostaticsFrancese
(f.) géostatiqueTedesco
(f.) Gleichgewichtslehrelunghezza.
(s.f.), 1 in geom. estensione di un segmento e la sua misura; è una delle tre dimensioni dei solidi. 2 la massima estensione di un oggetto e la misura che la rappresenta. 3 durata nel tempo.Inglese
lenghtFrancese
(f.) longueurTedesco
(f.) Längeocclusione.
(s.f.), 1 atto, effetto dell'occludere. 2 in chim. assorbimento di gas da parte di solidi.Inglese
occlusionFrancese
(f.) occlusionTedesco
(m.) Verschlußpicnòmetro.
(s.m.), apparecchio per determinare la densità di corpi solidi e liquidi.Inglese
pycnometerFrancese
(m.) pycnomètrestereometria.
(s.f.), branca della geometria che si occupa dei solidi.Inglese
stereometryFrancese
(f.) stéréométrieTedesco
(f.) Stereometrietotalrifrattometro.
(s.m.; ott.), strumento che misura l'indice di riflessione dei liquidi e dei solidi; è basato sul fenomeno della riflessione totale della luce.Inglese
total refractometerFrancese
(m.) réfractomètre totalTedesco
(n.) Totalreflektometervolumenòmetro.
(s.m.), in fis. strumento per la misurazione del volume dei corpi solidi.Inglese
volumenometerFrancese
(m.) voluménomètreTedesco
(n.) Volumenometerabbattuta.
(s.f.), 1 insieme di alberi abbattuti. 2 mar. rotazione che effettua una imbarcazione a vela per prendere il vento.Inglese
fellingFrancese
(m.) abattisABS.
(s.m.; ingl.) termine inglese con cui si indica negli autoveicoli, il sistema antibloccaggio delle ruote. Consiste in una centralina elettronica informata da un microprocessore e da sensori che misurano costantemente la velocità di rotazione delle ruote valutando l'eventuale tendenza a bloccarsi. In caso di frenata l'ABS interviene immediatamente, riducendo la pressione nel circuito frenante ed evitando ogni rischio di bloccaggio delle ruote. L'ABS costituisce un importante contributo per la sicurezza di guida e si rivela utilissimo in casi di frenate di emergenza, in particolare su fondi scivolosi.Inglese
ABSFrancese
ABSTedesco
ABSavvitaménto.
(s.m.), 1 l'avvitare, l'avvitarsi. 2 in ginnastica, rotazione del corpo su sé stesso.Inglese
spinFrancese
(m.) vissageTedesco
(f.) Verschraubungbaionétta.
(s.f.), 1 arma bianca che si può innestare sul fucile. 2 tecn. innesto a -: giunzione di due pezzi infilati uno nell'altro e fissati con una piccola rotazione.Inglese
bayonet.Francese
(f.) baïonnette.Tedesco
(n.) Bajonettcatenoide.
(s.f.), solido di rotazione generato da una catenaria.Francese
(f.) caténoïdeTedesco
(n.) Katenoidcircolazione.
(s.f.), 1 atto ed effetto del circolare: stradale, aerea; tassa di -, imposta che colpisce i possessori di autoveicoli motoveicoli natanti e aeromobili libretto di -, documento attestante l'avvenuto pagamento dell'imposta e la libera circolazione del mezzo. 2 in anat. - del sangue, il fluire del sangue dal cuore alle arterie, dalle arterie alle vene e dalle vene al cuore. 3 in fis. - atmosferica, il movimento costante dei venti dovuto all'irradiazione solare e alla rotazione terrestre.Inglese
circulationFrancese
(f.) circulationTedesco
(m.) Umlaufcirconduzione.
(s.f.), esercizio ginnico che prevede la rotazione del braccio teso intorno all'articolazione della spalla.Inglese
circlingFrancese
(f.) circumduction.Tedesco
(n.) Kreisencolt.
(s.m. ingl.), pistola a rotazione.Inglese
Colt revolverFrancese
(m.) coltTedesco
(m.) Coltcono.
(s.m.), 1 figura geometrica generata dalla rotazione di un triangolo rettangolo intorno ad uno dei cateti. 2 tutto ciò che ha forma di cono: un - di gelato. 3 in bot. frutto legnoso a forma di cono.Inglese
coneFrancese
(m.) côneTedesco
(m.) Kegelellissòide.
(s.m.), in geom. superficie ottenuta dalla rotazione di un'ellisse attorno ad uno dei suoi assi.Inglese
ellipsoidFrancese
(m.) ellipsoideTedesco
(n.) Ellipsoidfase.
(s.f.), 1 in astr. ognuno degli aspetti assunti da un pianeta durante la rotazione: - lunare, aspetti presentati dalla luna rispetto al Sole e alla Terra. 2 stato; momento caratteristico di un fenomeno: - di sviluppo; - di compressione di un motore; essere fuori fase, fig. trovarsi in un momento di sbandamento psichico o fisico. 3 differenza di -, in elettr. misura di sfasamento fra la corrente e la tensione in un circuito elettrico. 4 in chim. quantità di materia omogenea, separabile da un'altra.Inglese
stageFrancese
(f.) phaseTedesco
(f.) Phasefloppy disk o diskette o disco flessibile.
(s.m. ingl.), termine inglese usato nel campo dell'informatica per indicare un sottile disco di materiale plastico rivestito con uno strato magnetico su una o due facce e chiuso in una busta che lascia solo le aperture necessarie per metterlo in rotazione e leggerlo o scriverlo. E' governato da un drive e può avere un diametro di 3,5 pollici o 5,25 pollici. Il floppy può essere sia a faccia singola che a doppia faccia.Inglese
floppy diskFrancese
floppy diskTedesco
(f.) Diskettegiravolta.
(s.f.), 1 movimento di rotazione. 2 serpentina. 3 cambiamento improvviso di idee o di sentimenti.Inglese
twirlFrancese
(f.) pirouetteTedesco
(m.) Purzelbauparabolòide.
(s.m.), in geom. solido dato dalla rotazione di una parabola intorno al proprio asse.Inglese
paraboloidFrancese
(m.) paraboloïdeTedesco
(n.) Paraboloidperiodo.
(s.m.), 1 ognuna delle parti in cui può essere suddivisa la durata di qualcosa; spazio di tempo con caratteristiche determinate. 2 frasi musicali collegate; più proposizioni che formano un senso compiuto. 3 spazio di tempo necessario, in un moto oscillatorio, alternato, circolare, per ritornare nella posizione di partenza; tempo impiegato da un astro per compiere una rotazione o rivoluzione. 4 serie di elementi a numero atomico crescente.Inglese
periodFrancese
(f.) périodeTedesco
(f.) Zeitspannepiroetta.
(s.f.), 1 rapida rotazione del corpo su sé stesso. 2 figura di danza e del pattinaggio artistico; esercizio d'alta equitazione.Inglese
pirouetteFrancese
(f.) pirouetteTedesco
(f.) Pirouettepolo.
(s.m.), 1 ciascuno dei due punti in cui la superficie terrestre interseca l'asse di rotazione. 2 le regioni intorno ai poli. 3 posizione antitetica ad un'altra. 4 la proiezione dei poli terrestri sulla sfera celeste. 5 punto dotato di particolare caratteristica o simmetria. 6 estremità di un asse di simmetria di un organismo, di una cellula, ecc. 7 gioco disputato da due squadre a cavallo, le quali cercano di mandare nella porta avversaria una palla colpendola con una mazza. 8 indumento di maglia come quello indossato dai giocatori di polo.Inglese
poleFrancese
(m.)pôleTedesco
(m.)Polquarterìa.
(s.f.), in agr. la rotazione di quattro anni, con un anno a riposo o a maggese.Francese
(f.) assolement quadriennalrotativo.
(agg.), 1 dotato di movimento rotatorio. 2 che avviene per rotazione.Inglese
rotativeFrancese
rotatifTedesco
drehendrotazionale.
(agg.), della rotazione.Inglese
rotationalFrancese
rotationnelTedesco
Rotations...rotazione.
(s.f.), 1 movimento di un corpo intorno ad un altro o intorno al proprio asse. 2 avvicendamento, successione ordinata.Inglese
rotationFrancese
(f.) rotationTedesco
(m.) Umlaufsincronizzatore.
(s.m.), dispositivo che serve a sincronizzare due o più movimenti; in aer. dispositivo che permette di sparare attraverso la rotazione dell'elica senza colpire le pale.Inglese
synchronizerFrancese
(m.) synchroniseurTedesco
(m.) Synchronisierersnodo.
(s.m.), snodatura, giunto meccanico che permette movimenti di rotazione.Inglese
jointFrancese
(f.) articulationTedesco
(m.) Gelenkspin.
(s.m.), momento magnetico di rotazione delle particelle elementari e dei nuclei atomici.Inglese
spinFrancese
(m.) spinTedesco
(m.) Spinsplenio.
(s.m.), muscolo che riveste la parte posteriore della nuca e consente l'inclinazione e la rotazione del capo.Inglese
spleniusFrancese
(m.) spléniusTedesco
(m.) Kopfmuskeltoro.
(s.m.), 1 (mat.), superficie generata dalla rotazione di una circonferenza intorno ad una retta ad essa esterna. 2 (arch.), modanatura nel basamento di una colonna.Inglese
torusFrancese
(m.) toreTedesco
(m.) Thorustorsione.
(s.f.), 1 il torcere, il torcersi; rotazione del corpo umano attorno ai suo asse longitudinale: la - della testa; - del busto; elasticità di -, proprietà di alcuni corpi di riprendere la forma primitiva al cessare della sollecitazione di torsione. 2 (fis.), sollecitazione semplice che si ha in un solido quando l'azione esterna riduce ad una coppia di forze agenti nel piano della sezione.Inglese
torsionFrancese
(f.) torsionTedesco
(f.) Drehungcircŭmactus
ūs, m.: rotazione, rivoluzione (intorno ad un asse).![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()
