![]()
Prisma retto: Costruzione e Calcolo della Superficie Laterale
Cilindro: costruzione e calcolo della superficie laterale
Cilindro equilatero superficie e volume
Ripasso di matematica Geometria dello spazio
Aritmetica Geometria Informatica
Dizionario Lessicale di Geometria
Geometria Piana e Solida Informatica Media
![]()
![]()
Geometria Piana e Solida
Elementi Fondamentali della Geometria Gli Angoli Il Triangolo Il Cerchio Linee sul Piano Quadrilateri e Poligoni Superficie dei Poligoni Cilindri e Prismi Coni e Piramidi Gli Esaedri La Sfera Geometria Solida Nozioni Generali Solidi di Rotazione
![]()
![]()
PRISMA RETTO: Costruzione e Calcolo della Superficie Laterale.
Il prisma retto è una figura geometrica solida che ha due basi uguali e parallele e una superficie laterale perpendicolare alle basi, costituita da facce rettangolari.Le due basi possono essere poligoni diversi:
se sono triangoli, il prisma si chiama prisma triangolare e la sua superficie laterale ha 3 facce (quante sono i lati delle basi);
se sono pentagoni, è un prisma pentagonale e la sua superficie laterale ha 5 facce;
e così via.
Vediamo come si può costruire un prisma retto e, una volta costruito, come si fa a calcolare l'area della superficie laterale.
1. Costruiamo lo sviluppo di un prisma retto.
Vogliamo costruire lo sviluppo del prisma triangolare retto rappresentato in figura 1.
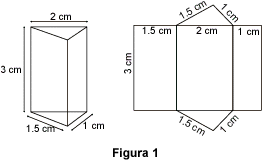
Le due basi del prisma sono triangolari e congruenti;
i loro lati misurano rispettivamente 1 cm, 1,5 cm e 2 cm.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
La superficie laterale comprende tre facce rettangolari che hanno la stessa base, uguale all'altezza del prisma:
3 cm.
Le altezze di queste facce sono rispettivamente uguali alle lunghezze dei lati della base:1 cm, 1,5 cm e 2 cm.
In figura 2 possiamo vedere un modello di prisma e la simulazione del suo montaggio.
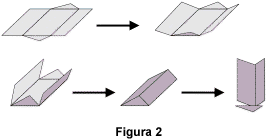
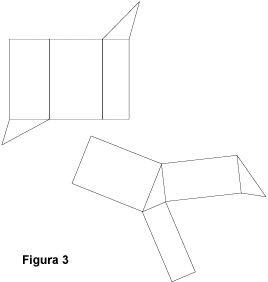
Nota:
Esistono diversi sviluppi di un prisma retto dato;
in figura 3 si vedono due possibili alternative.
L'area della superficie laterale di un prisma retto è la somma delle aree delle sue facce laterali.
2.1. Esempio.
Consideriamo il prisma della figura 1.
La sua area laterale è uguale all'area del rettangolo grande formato dall'insieme delle tre facce laterali;
questo misura 3 cm di altezza e 4,5 cm di base (1,5 + 2 + 1 = 4,5).
L'area laterale del nostro prisma retto sarà quindi uguale a 13,5 cm² (3 x 4,5 = 13,5).
Nota:
Si può sottolineare che la base del rettangolo grande (4,5 cm) è uguale al perimetro di ciascuna delle basi del prisma.
2.2. Caso generale.
L'area laterale A di un prisma retto, di altezza h e con le basi che hanno la lunghezza del perimetro uguale a P, è data dalla formula:
A = P x h.
Per applicare la formula, A, P e h devono essere espressi in unità di misura corrispondenti;
ad esempio:
A in cm², P in cm e h in cm.
3. Calcoliamo l'area della superficie totale di un prisma retto.
Una volta nota l'area A della superficie laterale, per trovare la superficie totale S basta sommare l'area delle due basi B.
Quindi, S = A + 2B.
Prisma retto e cilindro:
volume
Le aree laterali di un prisma retto e di un cilindro di rotazione si esprimono con la stessa formula:
A = P × h.
Come si calcola il volume di questi solidi?
1.
Calcoliamo il volume di un prisma retto.
1.1.
Formula
Il volume V di un prisma retto di altezza h e avente una base di area B (figura 1 ) è dato dalla formula:
V = B × h.
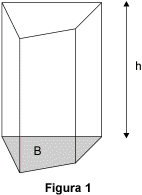
Per applicare questa formula, h, B e V devono essere espressi in unità di misura corrispondenti;
ad esempio:
se h è espresso in cm, B deve essere in cm² e V in cm³.
1.2.
Esempi.
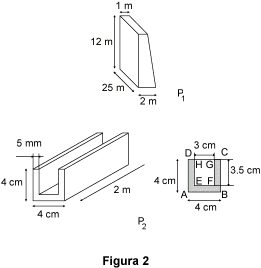
Vogliamo calcolare il volume dei due prismi retti rappresentati in figura 2.
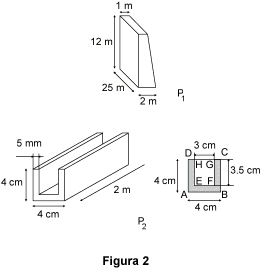
Prisma P1
Le sue basi sono dei trapezi (nella figura, il prisma non è appoggiato su una delle due basi, ma su una faccia della superficie laterale).
Calcoliamo l'area di un trapezio con la formula
![]()
con B = 2 m, b = 1 m e h = 12 m;
![]() ,
,
dunque l'area di base di un prisma è uguale a 18 m².
Calcoliamo allora il volume del prisma con la formula
V = B x h, dove B = 18 m² e h = 25 m;
18 x 25 = 450, quindi il volume del prisma è uguale a 450 m³.
Prisma P2
La base del prisma ha una forma a "U", come disegnata in figura.
Possiamo calcolare la sua area per differenza:
B=area(ABCD)-area(EFGH)=
= 16 cm² - 10,5 cm² =
= 5,5 cm² (4 x 4 =
= 16 ; 3 x 3,5 =
= 10,5 e 16 - 10,5 = 5,5).
Calcoliamo allora il volume del prisma con la formula V = B x h con
B = 5,5 cm² e h = 2 m = 200 cm;
5,5 x 200 = 1100,
dunque il volume del prisma è uguale a 1100 cm³.
2. Calcoliamo il volume di un cilindro di rotazione
2.1. Formula
Il volume V di un cilindro di rotazione di altezza h e di raggio R (figura 3) è dato dalla formula:
V = p x R x R x h
(p è il numero "pi greco", uguale a circa 3,14).
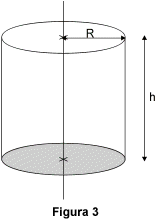
Se chiamiamo B l'area di base, ovvero l'area di un cerchio di raggio R, abbiamo:
B = p x R x R, e la formula precedente diventa:
V = B x h.
Per applicare questa formula, h, R, B e V devono essere espressi in unità di misura corrispondenti;
ad esempio:
h in cm, R in cm, B in cm² e V in cm³.
2.2. Esempio.
Calcoliamo il volume di un cilindro di rotazione di 5 cm e di altezza 10 cm:
p x 5 x 5 = 25p;
quindi l'area di base B è uguale 25p cm².
25p x 10 = 250p;
quindi il volume V del cilindro è uguale a 250p cm³, che all'incirca è 785 cm³.
Cilindro: costruzione e calcolo della superficie laterale.
Il cilindro è un solido di rotazione.
Ciò significa che, idealmente, lo si può ottenere dalla rotazione di una figura piana intorno a uno dei suoi lati.
In particolare, il cilindro retto si ottiene dalla rotazione di un rettangolo intorno a uno dei suoi lati.
Il cilindro retto ha per basi due cerchi uguali e paralleli, e per superficie laterale un rettangolo.
Lo vediamo bene se costruiamo il cilindro con un foglio di cartoncino:
si disegna il suo sviluppo sul foglio, poi lo si taglia e lo si piega.
Qual è il metodo per costruire lo sviluppo del cilindro e come si fa a calcolare l'area della superficie totale del cilindro?
1. Costruiamo lo sviluppo di un cilindro di rotazione.
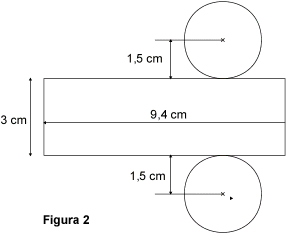
Vogliamo costruire lo sviluppo del cilindro di rotazione rappresentato in figura 1.
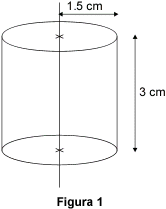
Le basi del cilindro sono due dischi di 1,5 cm di raggio ciascuno.
Lo sviluppo della superficie laterale è rettangolare;
i due lati del rettangolo sono uguali, rispettivamente, all'altezza del cilindro (3 cm) e alla circonferenza dei dischi di base.
Per calcolare questo perimetro, cioè la lunghezza della circonferenza, applichiamo la formula P = 2 × p × R, dove P, p e R sono rispettivamente il perimetro, il numero pi greco (circa 3,14) e il raggio.
Otteniamo che P = 2 × 3,14 × 1,5 = 9,42.
La lunghezza della circonferenza di base è dunque uguale a circa 9,4 cm.
Nelle figure 2 e 3 possiamo vedere lo sviluppo di un cilindro e i passaggi per il montaggio.
Nota:
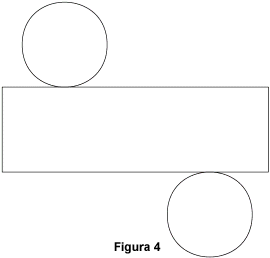
Esistono anche altri sviluppi di un cilindro di rotazione;
in figura 4 vediamo un altro modo di disegnarlo.
2. Calcoliamo l'area laterale di un cilindro di rotazione.
Lo sviluppo della superficie laterale di un cilindro è una superficie rettangolare.
L'area laterale di un cilindro è uguale all'area di questa superficie rettangolare.
2.1. Esempio.
Consideriamo il cilindro di rotazione della figura 1 e uno dei suoi sviluppi.
L'area laterale del cilindro è uguale all'area del rettangolo sviluppato.
Questo rettangolo misura 3 cm di larghezza e 3 p cm di lunghezza (2 × p × 1,5 = 3 p).
La sua area sarà quindi uguale a 3 × 3 p cm2, cioè 9 p cm2, ovvero circa 28,27 cm².
2.2. Caso generale.
L'area laterale A di un cilindro di rotazione di altezza h e di raggio R è dato dalla formula:
A = 2 × p× R × h ;
A = P × h (P indica il perimetro di una base).
Per applicare questa formula, A, R, h e P devono essere espressi nell'unità di misura corrispondente;
ad esempio, A in cm², R in cm, h in cm e P in cm.
Nota:
La formula A = P × h si applica anche al calcolo della superficie laterale di un prisma retto.
3. Calcoliamo l'area totale di un cilindro di rotazione.
L'area totale S di un cilindro di rotazione è data dalla somma dell'area laterale A e dell'area delle due basi B.
Poiché l'area di una base è
B = p R2, avremo:
S = A + 2B =
= 2 p R h + 2 p R2 =
= 2 p R (h + R)
Sinonimo:
cilindro
(s.m. Corpo geometrico tridimensionale che ha come basi due circonferenze uguali), bobina, cannello, rullo, spola. cilindrico
(agg.), tubolare.
cilindrico
(agg.), tubolare.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()