![]()
Solidi di rotazione
La lattina di una bibita, la punta di una matita e un pallone sono corpi geometrici che possiedono una parte della loro superficie, o tutta quanta, curva. La lattina è un cilindro, la punta della matita è un cono, il pallone è una sfera. A questi tre corpi, il cilindro, il cono e la sfera, si dà il nome di solidi rotondi, o solidi di rotazione.
IL CILINDRO
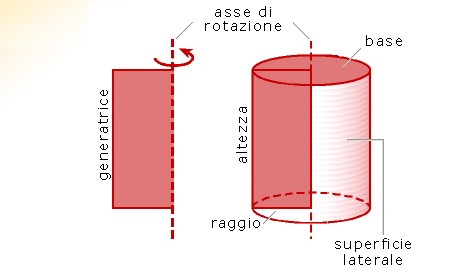
Le colonne di un tempio classico, il mattarello e il rullo di un compressore stradale sono altri esempi di cilindri. Il cilindro si forma facendo ruotare un rettangolo attorno a uno dei sui lati, che si mantiene in posizione fissa, come una porta girevole. Gli elementi del cilindro sono:
Le basi: sono due cerchi uguali.
Il raggio del cilindro: è il raggio delle basi.
L'asse di rotazione: è la retta immaginaria su cui si trova il lato attorno al quale il rettangolo gira per formare il cilindro.
La generatrice: è il lato del rettangolo opposto all'asse di rotazione.
L'altezza del cilindro: è la lunghezza della generatrice.
La superficie laterale: è la faccia curva del cilindro.
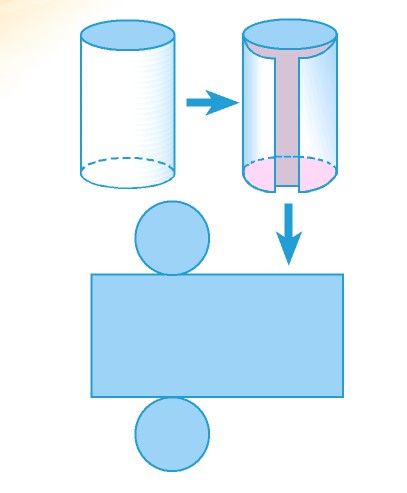
Se tagliamo un cilindro lungo la superficie laterale, in verticale, e lungo i bordi delle basi, e lo distendiamo su un piano, otteniamo questo sviluppo:
![]()
![]()
IL CONO
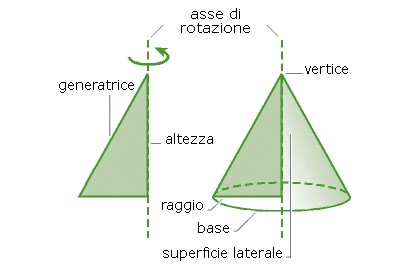
Il cono di un gelato e il tetto di una capanna sono esempi di coni. Il cono si forma facendo ruotare un triangolo rettangolo attorno a uno dei suoi cateti. Gli elementi del cono sono:
La base: è il cerchio su cui poggia.
Il raggio del cono: è il raggio della base.
Il vertice: è la cuspide o picco del cono.
La generatrice: è l'ipotenusa del triangolo rettangolo che ruotando forma il cono, oppure, in modo equivalente, qualunque segmento tracciato tra il vertice del cono e un punto della circonferenza della base.
L'asse di rotazione: è la retta immaginaria su cui si trova il cateto attorno a cui gira il triangolo rettangolo per formare il cono.
L'altezza: è la lunghezza del cateto su cui gira il triangolo rettangolo.
La superficie laterale: è la faccia curva del cono.
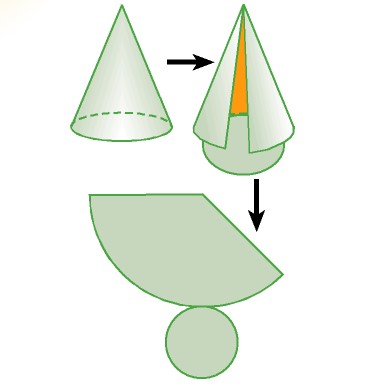
Se tagliamo il cono lungo la superficie laterale, seguendo la generatrice, e lungo il bordo della base, e lo distendiamo su un piano, otteniamo questo sviluppo:
![]()
![]()
LA SFERA
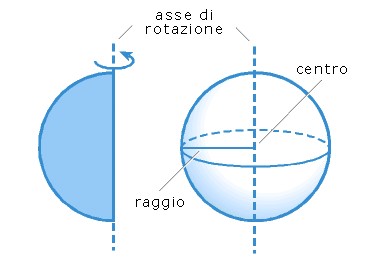
Un pallone da calcio, un'arancia e una biglia sono esempi di sfere. La sfera si forma dalla rotazione di un semicerchio attorno al suo diametro. I principali elementi di una sfera sono il centro e il raggio.
La sfera non è dotata di uno sviluppo piano, come gli altri corpi geometrici.
Tagliando una sfera in modi diversi, con superfici piane, otteniamo diverse figure: l'emisfero, la calotta sferica e la zona sferica.
L'emisfero si trova se dividiamo a metà una sfera.
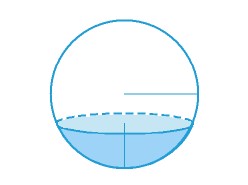
La calotta sferica si ottiene se tagliamo la sfera con una sola superficie piana, non passante per il centro. Nella Terra, che è praticamente una sfera, chiamiamo calotte polari le due calotte situate al Polo Nord e al Polo Sud.
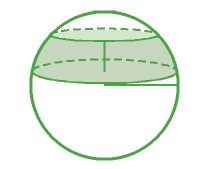
La zona sferica si trova se tagliamo la sfera con due superfici piane e parallele.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
LA SFERA TERRESTRE
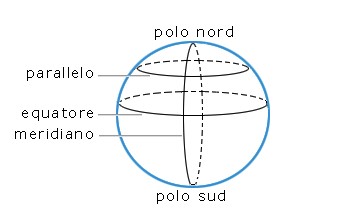
Siccome la Terra ha una forma quasi sferica (è un po' schiacciata ai poli), la chiamiamo sfera terrestre.
Sulla sua superficie, tracciamo delle linee immaginarie, che ci permettono di indicare la posizione di un qualunque punto su di essa, per esempio, la posizione del tuo paese o città. Queste linee sono: l'asse terrestre, l'equatore, i paralleli e i meridiani.
L'asse di rotazione, o asse terrestre, è l'asse ai cui estremi sono situati il Polo Nord e il Polo Sud.
L'equatore è la circonferenza massima, perpendicolare all'asse terrestre.
I paralleli sono circonferenze parallele all'equatore, ma minori di esso.
I meridiani sono le circonferenze che uniscono i poli. Si chiama meridiano zero quello che passa da Greenwich, che è una cittadina inglese nei pressi di Londra.
Microsoft ® Encarta ®
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()