Youmath La Sfera Andreaminini La Sfera Impariamo insieme La Sfera Sapere virgilio Le Sfere definizione superficie e volume Risolvi geometria formule La Sfera
![]()
Ripasso di matematica Geometria del piano euclideo
Prisma retto Cilindro Superficie e Volume Aritmetica Geometria Informatica Dizionario Lessicale di Geometria
Geometria Piana e Solida Informatica Media
GEOMETRIA PIANA E SOLIDA
Elementi Fondamentali della Geometria Gli Angoli Il Triangolo Solidi di rotazione Linee sul Piano Quadrilateri e Poligoni Superficie dei Poligoni Cilindri e Prismi Coni e Piramidi Gli Esaedri Il Cerchio Geometria Solida Nozioni Generali Solidi di Rotazione
![]()
![]()
GEOMETRIA SOLIDA - LA SFERA
PROPRIETA' GEOMETRICHE
La sfera è senz'altro il solido più comune nell'universo che ci circonda:basta pensare all'infinità delle stelle e dei pianeti.
Dal punto di vista geometrico:
La sfera è un solido di rotazione generato da un semicerchio che ruota attorno al proprio diametro.
Si chiama superficie sferica la superficie che la delimita;
il raggio della semicirconferenza generatrice prende il nome di raggio della sfera.
Infatti la sfera gode della seguente importante proprietà:
Tutti i punti di una superficie sferica hanno la medesima distanza da un punto fisso detto centro:
tale centro coincide con quello della semicirconferenza generatrice, e la distanza corrisponde al raggio.
Tutte le sezioni di una sfera sono cerchi;
il piano passante per il centro interseca la sfera secondo il cerchio massimo, così chiamato perché il suo raggio, uguale a quello della sfera, è maggiore di quello di tutte le sezioni che non contengono il centro.
Ogni retta passante per il centro è un asse e incontra la superficie sferica in due punti P' e P" detti poli.
Vale la seguente proprietà:
Per due poli passano infinite circonferenze massime dette meridiani.
Il piano perpendicolare all'asse interseca la superficie sferica secondo circonferenze dette paralleli:
fra queste ve n'è una di diametro massimo detta equatore.
PARTI DELLA SFERA
Consideriamo due sezioni parallele di una sfera:esse delimitano una porzione del solido fra due basi b e B detta segmento sferico;
si chiama invece zona sferica la porzione di superficie sferica che la racchiude lateralmente.
In un segmento sferico possiamo distinguere i raggi r' ed r" delle basi stesse e un'altezza 0'0" che è la distanza fra le basi.
Immaginiamo ora di allontanare dal centro il piano :
la base b diventerà sempre più piccola fino a diventare un punto.
Diremo allora che il piano Y è tangente alla sfera, e avremo un segmento sferico a una sola base, la cui superficie costituisce una calotta sferica.
In altre parole:
Un piano secante divide la sfera in due parti dette segmenti sferici (a una base) e la superficie sferica in due calotte.
Se il piano secante passa per il centro della sfera, i due segmenti in cui questa è divisa risultano uguali e si dicono emisferi.
In geografia si divide, ad esempio, la Terra in due parti al di sopra e al di sotto dell'equatore, dette rispettivamente emisfero settentrionale ed emisfero meridionale.
Consideriamo infine due semipiani aventi per origine un asse della sfera:
essi formano un diedro che racchiude una porzione detta spicchio sferico;
si chiama fuso sferico la porzione di superficie sferica appartenente allo spicchio.
Il valore dell'angolo diedro fra le due facce piane costituisce l'ampiezza dello spicchio o del fuso.
Osserviamo che il volume dello spicchio e l'area del fuso sono proporzionali all'ampiezza:
l'intera sfera può considerarsi uno spicchio con ampiezza di 360°, mentre uno spicchio di 180° costituisce un emisfero.
![]()
![]()
AREA DELLA SUPERFICIE SFERICA
Abbiamo già visto che una superficie di rotazione non e sviluppabile su un piano quando la sua generatrice è una linea curva:
e la sfera obbedisce a tale regola.
Come per tutte le superfici di rotazione, esistono però particolari metodi che ci consentono di calcolare il valore dell'area e quindi di confrontarla con quella di superfici piane.
Del resto, senza ricorrere a questi metodi, fin dall'antichità era nota la seguente legge:
L'area della superficie sferica è uguale a quella della superficie cilindrica ad essa circoscritta.
Precisiamo che per «superficie cilindrica circoscritta a una sfera» si intende la superficie laterale del cilindro retto avente diametro di base e altezza uguali fra loro e al diametro della sfera (cfr. «Volume della sfera», fig. 357).
Ricordando la formula dell'area laterale del cilindro si ha:
A S = A l =
= 2p R*2R =
= 4p R2
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
VOLUME DELLA SFERA
Consideriamo una porzione di superficie sferica (fig. 358) così piccola da poter essere considerata piana.Ricorda che anche la superficie terrestre è tanto estesa da sembrare piana ai nostri occhi.
Possiamo immaginarla come la base di un cono, avente per direttrice il suo contorno e il centro della sfera come vertice, con altezza pari al raggio.
Se indichiamo con A l'area della base, il volume del cono sarà:
1
V = - AR
3
Figg. 357, 358 e 359
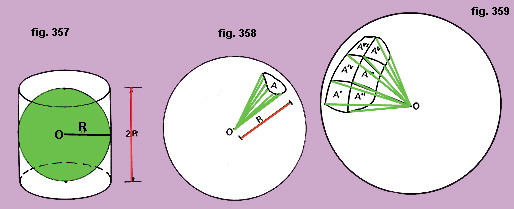
Immaginiamo di costruire tanti piccoli coni come quello di fig. 358 ravvicinati finché le loro basi non avranno coperto completamente la superficie sferica:
a questo punto anche i loro volumi sommati avranno riempito esattamente lo spazio occupato dalla sfera (fig. 359)
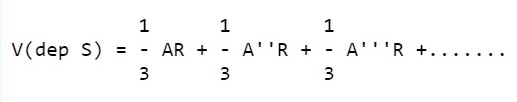
Ora, i coni hanno tutti la stessa altezza: sono quindi equivalenti a un unico cono avente quell'altezza e per base l'insieme delle basi, equivalente a sua volta alla superficie sferica. In conclusione:
La sfera è equivalente a un cono avente per base la sua superficie e per altezza il suo raggio:
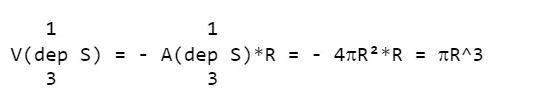
VERO O FALSO?
1) Due segmenti ricavati dalla stessa sfera, se hanno la stessa altezza, hanno uguale volume.2) La sfera è equivalente al cilindro circoscritto.
3) L'area della superficie sferica è quattro volte l'area del cerchio massimo.
4) I paralleli dividono la superficie sferica in fusi.
5) Due calotte ricavate dalla stessa superficie sferica hanno la stessa area se hanno la stessa altezza
1) Falso:
hanno zone sferiche equivalenti.
2) Falso:
la superficie sferica e equivalente a quella laterale del cilindro circoscritto.
3) Vero.
4) Falso: la dividono in zone sferiche.
5) Vero.
ESERCIZI
1) Calcolare l'area del cuoio di un pallone da football del diametro di cm 25.Se il diametro è di cm 25, il raggio misura cm (25:2) = cm 12,5.
Applichiamo la (1)
S = cm2 (4*3,14*12,52) = cm2 1962,5
2) La sfera di ferro usata in atletica dai lanciatori pesa circa 4 kg.
Calcolare il suo raggio sapendo che il peso specifico del ferro è 7,8.
Calcoliamo dapprima il volume:
V = dm3 (4:7,8) = dm3 0,50126 = cmc 501,26
Ora applichiamo la (2) inversa:

3) Calcolare l'area di una calotta alta m 15 appartenente a una sfera di m 40 di raggio. Applichiamo la (3):
![]()
4) Calcolare il volume di uno spicchio sferico di raggio m 20 e ampiezza 45°. Applichiamo la (8):
![]()
5) Calcolare l'ampiezza di un fuso appartenente alla sfera dell'esercizio precedente la cui area misura m2 8373,4.
Applichiamo la (7) inversa:
![]()
Tabella riassuntiva della sfera
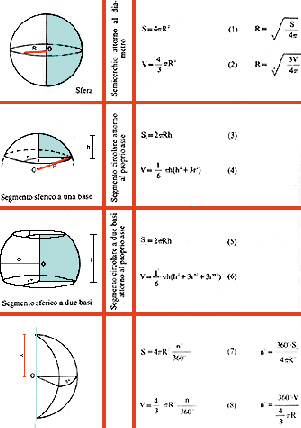
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()
