![]()
News notizie del giorno Online Newspapers
I media e la Teoria degli Insiemi:
Lezioni ignoranti altervista.org Storia della teoria degli insiemi Easy-test.it Insiemi concetti fondamentali e applicazioni pratiche Users di Uniroma1.it Dispense Top esempi.com Insiemi matematici Extrabyte.info Lezioni di matematica teoria degli insiemi Competenza matematica.it Dalla teoria ingenua alla teoria assiomatica degli insiemi Ams laurea Unibo.it Matematica in rete.it Insiemi e funzioni Studocu.com Teoria degli insiemi Cird Unical.it Teoria degli insiemi Divulgazione libera.it Dmif Uniud.it Teoria degli insiemi Roberto Capone.com Insiemi Archivio multimedia Unict.it Teoria degli insiemi Daniele Baldissin altervista.org Problemi sugli Insiemi Informati Sardegna.it Teoria degli insiemi Science Unitn.it Assiomi Spiegato.com Cos'é la teoria degli insiemi Sites Unipa.it Valerio La Cagnina Elementi teoria Insiemi Elearning Unite.it insiemi Schemi di matematica.it insiemi Brofferio.it Simboli insiemistica Mi imati Cnr.it People dm unipi.it Insiemi Staticmy Zanichelli.it Skuola.net Teoria degli insiemi Geogebra.org Set theory Afsu.it La teoria ingenua degli insiemi Parte-I Matematicamente.it insiemi Sapere virgilio.it Matematica oltre altervista.org La misteriosa storia della teoria degli insiemi Okpedia.it Teoria degli insiemi Mat Uni Roma2.it Gavarini dispense Resmini Library weschool.com Rapidtables.org Set Symbols Simatematica.it insiemi Poisson.phc.dm.unipi.it Del Vigna Teoria degli insiemi Dsps Uni Ct.it La Teoria degli Insiemi (2) Ripmat.it Teoria degli insiemi Youmath Lezioni di matematica You Tube Andrea Minini Sos Matematica Skuola Schemi di Matematica Si Matematica Altramatica Altervista Word Wall Impariamo Insieme Formuliamo Sostegno 20 Matemati Capovolta Qui Matematica Mate Mania Il genio della matematica altervista Matematica facile Ubimath Matepratica Matematica Scuola Formuliamo Matematika Matematica Facile Edu boom Okpedia Symbo Lab Pianeta Bambini Scuola Elettrica
![]() Matematica
Uni Roma La teoria degli insiemi
Matematica
Uni Roma La teoria degli insiemi
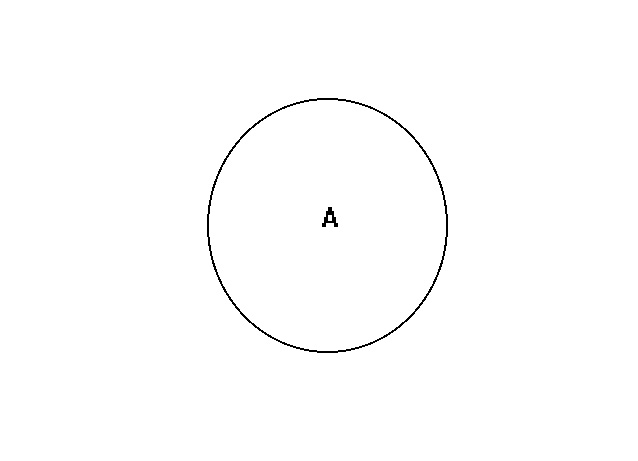
Diagramma di Eulero-Venn rappresentante l'insieme A
Relazione di inclusione Relazione di inclusione con il diagramma di Eulero-Venn Rappresentazione grafica di Eulero-Venn di due insiemi disgiunti
Operazione di unione Rappresentazione grafica di Eulero-Venn dell'insieme A U B Rappresentazione grafica di Eulero-Venn di insiemi disgiunti Rappresentazione di Eulero-Venn di insieme contenuto (unione) con un suo sottoinsieme
Operazione di intersezione Rappresentazione grafica di Eulero-Venn dell'intersezione di due insiemi Rappresentazione mediante i diagrammi di Eulero-Venn dell'uguaglianza di più insiemi Rappresentazione grafica mediante diagrammi di Eulero-Venn della parte in comune di più insiemi Rappresentazione grafica mediante diagrammi di Eulero-Venn di insieme unione;la proprietà distributiva
Differenza fra insiemi Rappresentazione grafica di Eulero-Venn di insiemi differenza
L'Insieme universo Rappresentazione grafica di Eulero-Venn dell'insieme universo
L'Insieme complementare Rappresentazione grafica di Eulero-Venn dell'insieme complementare o il complementare Rappresentazione grafica di Eulero-Venn sulle proprietà e le operazioni degli insiemi Rappresentazione grafica di Eulero-Venn insiemi non necessariamente disgiunti
Prodotto cartesiano fra due insiemi Rappresentazione grafica su diagramma cartesiano del prodotto di insiemi
Insieme delle parti o insieme potenza
Ripasso di matematica Teoria degli Insiemi
Aritmetica Geometria Informatica
Geometria Piana e Solida Informatica
Geometria Quadrilateri e Poligoni
Geometria Solida Nozioni Generali
![]()
![]()
MATEMATICA - TEORIA DEGLI INSIEMI
INTRODUZIONE
La teoria degli insiemi riveste un'importanza fondamentale nella matematica moderna in quanto ha applicazioni in algebra, logica, statistica, teoria delle probabilità, ecc. Generalizzando l'idea di insieme numerico possiamo introdurre il concetto generale di insieme in questo modo: "un insieme è una collezione finita o infinita di oggetti". E' importante tener presente che la natura degli "oggetti" e le regole e i principi per i quali questi oggetti vengono inseriti nell'insieme sono di secondaria importanza. Le operazioni e i teoremi sugli insiemi valgono indipendentemente dagli oggetti e dalle regole con cui questi insiemi sono costruiti. Un insieme che ha un numero "finito" di elementi (cioè 5, 10, 100, 3000 elementi) si dice "insieme limitato"; un insieme che ha un numero infinito di elementi (come, per esempio, l'insieme dei multipli di 2) si dice "insieme illimitato". Un insieme che non contiene nessun elemento si chiama insieme vuoto e si indica col simbolo Æ . L'idea di considerare una collezione di nessun elemento come un insieme può destare qualche perplessità, ma l'insieme vuoto è l'analogo per gli insiemi dello "zero", cioè un numero che non ha nessun valore per i numeri e vedremo che l'insieme vuoto sarà utilissimo quando introdurremo le operazioni con gli insiemi. Come i numeri reali, che possono essere rappresentati come punti di una retta, anche gli insiemi hanno una rappresentazione grafica nota con il nome di "rappresentazioni o diagrammi di Eulero-Venn". In pratica un qualsiasi insieme A viene rappresentato con un cerchio: la parte interna del cerchio rappresenta gli elementi di A, i quali possono non essere necessariamente specificati, mentre gli elementi che non appartengono all'insieme A sono rappresentati dalla parte esterna al cerchio. L'insieme vuoto non ha rappresentazione. Vedremo in seguito che nonostante l'estrema semplicità dei diagrammi di Eulero-Venn essi saranno utilissimi per dimostrare alcune delle proprietà più importanti degli insiemi.
Diagramma di Eulero-Venn rappresentante l'insieme A
![]()
![]()
RELAZIONE DI INCLUSIONE
Se ogni elemento di un insieme A è anche elemento di un altro insieme B allora si dice che "A è contenuto in B" e si indica "A É B".
Per esempio prendiamo i due insiemi numerici A = {1, 3, 5, 7, 9} e B = {1, 2, 3, 4, 5, 6, 7, 8, 9} (ricordiamo che gli insiemi presentati per "elencazione", cioè elencando tutti gli elementi dell'insieme, vanno messi fra parentesi graffa e ogni elemento deve essere separato dagli altri da una virgola) si vede che ogni elemento dell'insieme A è anche elemento dell'insieme B.
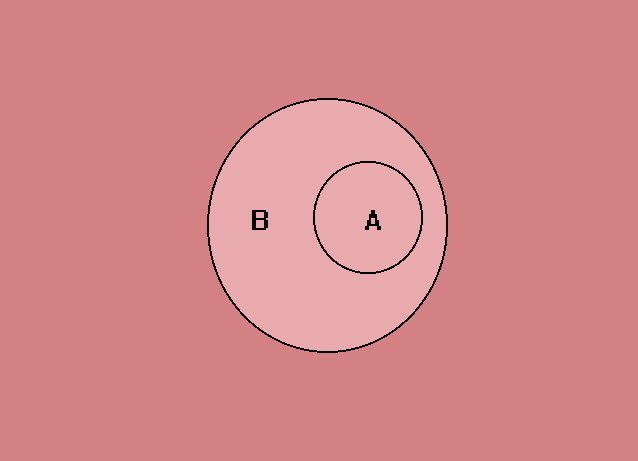
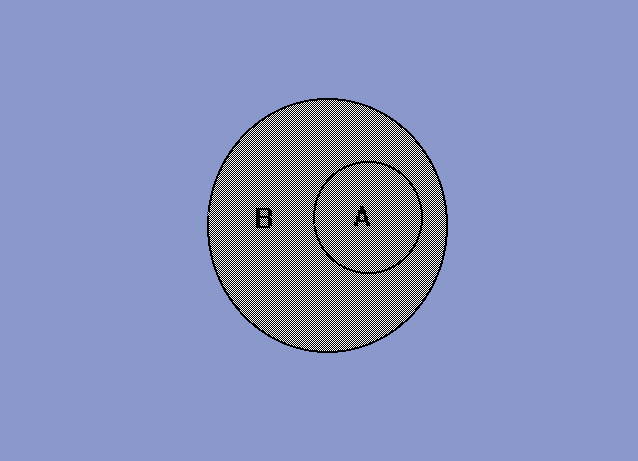
Con i diagrammi di Eulero-Venn la relazione di inclusione viene rappresentata come in figura 2.
Fig. 2 rappresenta la relazione di inclusione con il diagramma di Eulero-Venn
Se tutti gli elementi dell'insieme A sono tutti e i "soli" elementi dell'insieme B allora l'insieme A è uguale all'insieme B cioè A = B.
Due insiemi sono dunque uguali quando valgono contemporaneamente le due relazioni di inclusione: A É B e B É A. Quando un insieme A è contenuto (o uguale) in un insieme B si dice che "l'insieme A è sottoinsieme dell'insieme B".
Facciamo un altro esempio:
sia B l'insieme di tutte le auto circolanti con targa italiana e sia A l'insieme di tutte le auto circolanti con targa Milano.
E' evidente che l'insieme B contiene l'insieme A, in quanto le auto circolanti con targa Milano sono a sua volta auto con targa italiana.
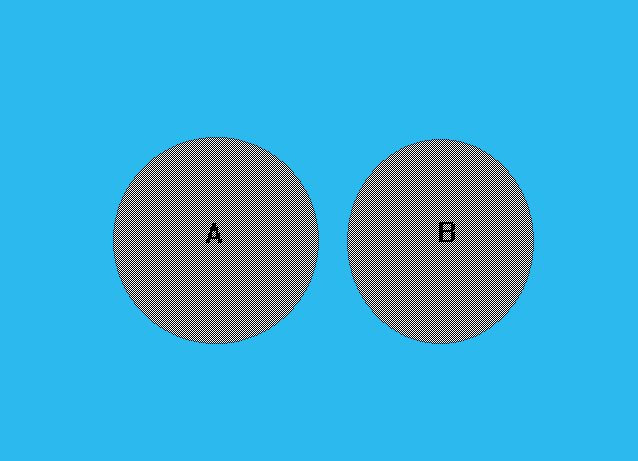
Se due insiemi non hanno nessun elemento in comune si dice che i due insiemi sono "disgiunti".
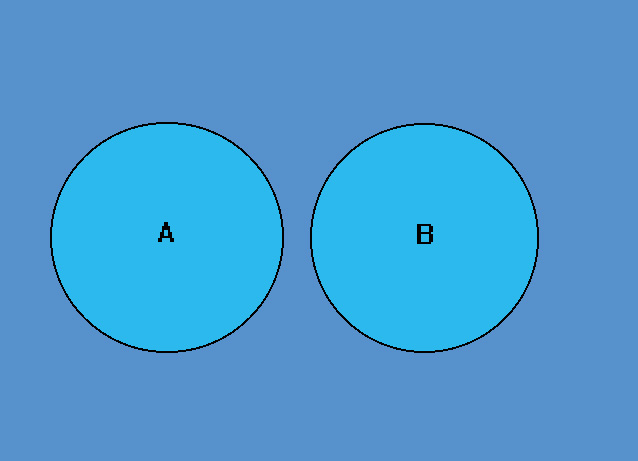
La rappresentazione grafica di Eulero-Venn di due insiemi disgiunti è quella in figura 3.
Fig. 3 rappresentazione grafica di Eulero-Venn di due insiemi disgiunti
OPERAZIONE DI UNIONE
L'operazione di unione fra due insiemi A e B si indica A U B e ha come risultato un insieme C i cui elementi sono sia gli elementi dell'insieme A sia gli elementi dell'insieme B contati però una volta sola.
Per esempio sia l'insieme A = {1, 2, 3, 4, 5} e l'insieme B = {1, 3, 5, 7, 9}; allora A U B = C dove l'insieme C = {1, 2, 3, 4, 5, 7, 9} e non C = {1, 1, 2, 3, 3, 4, 5, 5, 7, 9}.
Nella rappresentazione grafica di Eulero-Venn abbiamo che l'insieme A U B è rappresentato dalla zona evidenziata in figura 4.
Fig. 4 rappresentazione grafica di Eulero-Venn dell'insieme A U B
Se chiamiamo P l'insieme dei numeri interi pari con lo zero incluso (insieme illimitato) e D l'insieme dei numeri interi dispari, allora P U D = N dove N è l'insieme dei numeri interi.
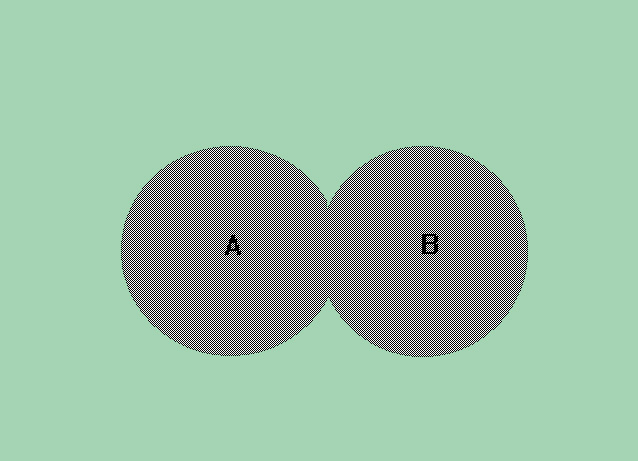
Se gli insiemi sono disgiunti, come nel caso degli insiemi P e D che non hanno nessun elemento in comune (un numero intero non può essere contemporaneamente pari e dispari - lo zero è considerato pari-), la rappresentazione di Eulero-Venn è quella evidenziata in figura 5.
Fig. 5 rappresentazione grafica di Eulero-Venn di insiemi disgiunti
Se l'insieme A è contenuto nell'insieme B allora dalla rappresentazione di Eulero-Venn si ricava che A U B = B cioè che l'unione di un insieme B con un suo sottoinsieme A è sempre uguale all'insieme B (vedi figura 6).
E' quindi possibile una definizione alternativa di sottoinsieme di un insieme:
A è sottoinsieme dell'insieme B se e solo se A U B = B.
Fig. 6 rappresentazione di Eulero-Venn di insieme contenuto (unione) con un suo sottoinsieme
Valgono anche le seguenti proprietà:
A U A = A - Proprietà riflessiva:
l'insieme A è sottoinsieme di se stesso
A U B = B U A - Proprietà commutativa: non importa l'ordine con cui si esegue l'operazione di unione
A U ( B U C) = (A U B ) U C - Proprietà associativa:
mediante questa proprietà è possibile definire l'operazione di unione per più di due insiemi.
A U Æ = A - L'insieme vuoto è un sottoinsieme di qualsiasi insieme
Æ U Æ = Æ - L'unione di due insiemi vuoti dà sempre un insieme vuoto
OPERAZIONE DI INTERSEZIONE
L'operazione di intersezione di due insiemi A e B si indica A Ç B ed è un insieme che contiene gli elementi che appartengono sia all'insieme A che all'insieme B.
In altre parole nell'insieme intersezione ci sono gli elementi comuni sia all'insieme A che all'insieme B.
Se per esempio prendiamo A = {1, 2, 3, 4, 5, 6, 7, 8, 9} e B = {1, 3, 5, 7, 9, 11, 13, 15, 17} allora A Ç B = C dove C = {1, 3, 5, 7, 9} infatti gli elementi dell'insieme C appartengono sia all'insieme A che all'insieme B.
Come altro esempio prendiamo l'insieme A come l'insieme di tutti i cittadini italiani e come insieme B l'insieme di tutti gli uomini la cui altezza è superiore ai 180 cm;
allora l'insieme C = A Ç B è l'insieme di tutti i cittadini italiani maschi che sono alti più di 180 cm.
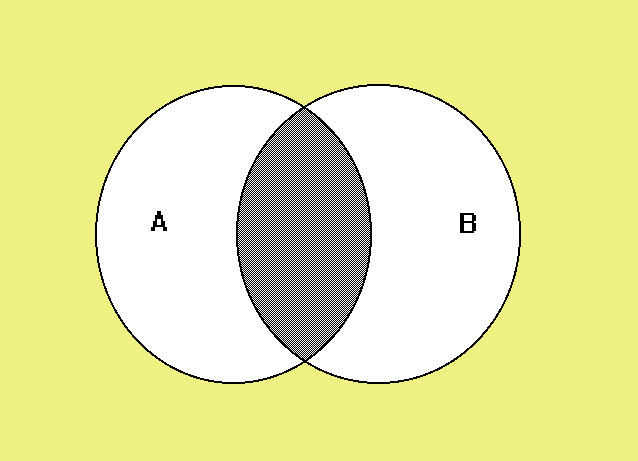
La rappresentazione grafica di Eulero-Venn dell'intersezione di due insiemi A e B è quella della figura 7 in cui l'insieme intersezione è evidenziato.
Fig. 7 rappresentazione grafica di Eulero-Venn dell'intersezione di due insiemi
L'insieme C = A Ç B risulta essere sottoinsieme sia dell'insieme A che dell'insieme B. Appare altresì evidente che se gli insiemi A e B sono disgiunti A Ç B = Æ e che se l'insieme A è contenuto nell'insieme B allora A Ç B = A, ovvero "l'intersezione fra un insieme B e un suo sottoinsieme A è sempre uguale al sottoinsieme A", cioè se A Ì B allora A Ç B = A che è un'altra definizione di sottoinsieme.
Valgono anche le seguenti proprietà:
A Ç A = A - Proprietà riflessiva:
A è sottoinsieme di se stesso
A Ç B = B Ç A - Proprietà commutativa: non importa l'ordine con cui si esegue l'operazione di intersezione
A Ç= Æ - L'insieme vuoto è un sottoinsieme di qualsiasi insieme
A Ç ( B Ç C ) = ( A Ç B ) Ç C - Proprietà associativa:
questa proprietà permette di definire l'operazione di intersezione per più di due insiemi.
Le operazioni di unione e di intersezione fra insiemi godono della proprietà distributiva:
A U ( B Ç C ) = ( A U B ) Ç ( A U C ) e
A Ç ( B U C ) = ( A Ç B ) U ( A Ç C )
Dimostriamo mediante i diagrammi di Eulero-Venn la prima uguaglianza lasciando la dimostrazione della seconda come esercizio.
Supponiamo per iniziare che i tre insiemi A, B e C siano tutti disgiunti e determiniamo l'insieme A U (B Ç C).
Poiché gli insiemi B e C sono disgiunti allora B Ç C = Æ e quindi A U ( B Ç C ) = A U Æ = A.
Il primo membro dell'uguaglianza è dunque l'insieme A.
Determiniamo ora l'insieme (A U B) Ç (A U C).
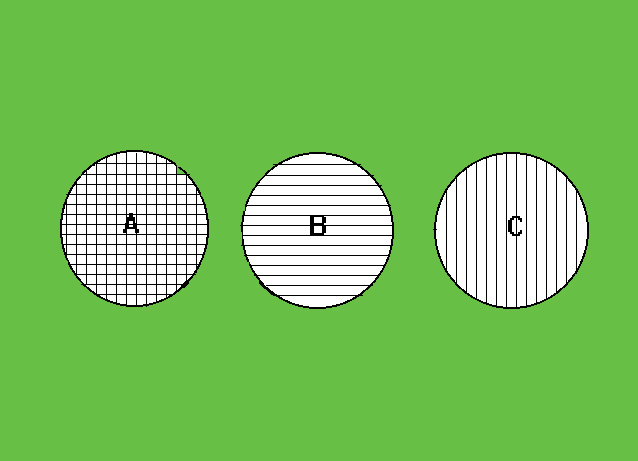
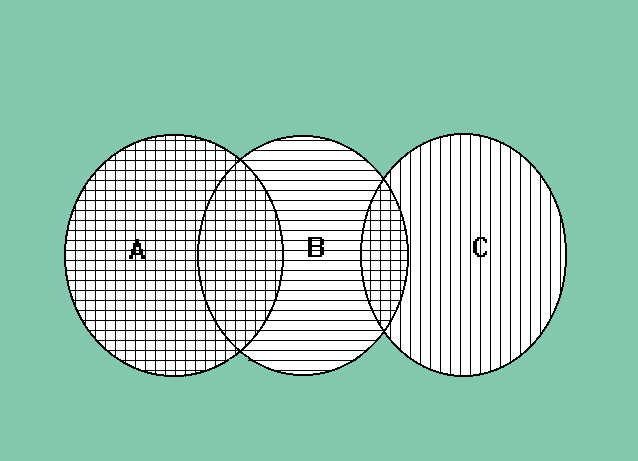
Nella rappresentazione grafica di Eulero-Venn l'insieme (A U B) è evidenziato con le righe orizzontali, mentre l'insieme (A U C) è evidenziato con le righe verticali.
L'insieme (A U B) Ç (A U C) sarà quindi l'insieme evidenziato nel diagramma di Eulero-Venn dalle righe orizzontali e verticali cioè proprio l'insieme A (vedi figura 8).
Quindi per insiemi disgiunti A U (B Ç C) = A = (A U B) Ç (A U C) vale la proprietà distributiva.
Fig. 8 rappresentazione mediante i diagrammi di Eulero-Venn dell'uguaglianza di più insiemi
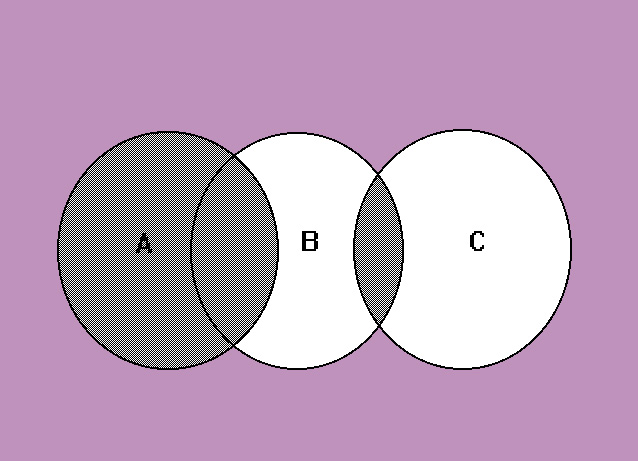
Siano ora A, B e C insiemi non necessariamente disgiunti come quelli rappresentati in figura 9;
allora l'insieme A U (B Ç C) è quello evidenziato in scuro, infatti B Ç C è la parte comune degli insiemi B e C unita poi con l'insieme A.
Determiniamo adesso l'insieme (A U B) Ç (A U C); l'insieme A U B è quello evidenziato con le righe orizzontali nel diagramma di Eulero-Venn della figura 10, mentre l'insieme A U C è evidenziato con le righe verticali.
L'insieme unione dei due insiemi è quello evidenziato contemporaneamente da righe verticali e orizzontali ed è chiaramente lo stesso insieme visto nella figura precedente.
Quindi anche per insiemi non necessariamente disgiunti la proprietà distributiva vale e quindi vale per qualsiasi insieme.
Fig. 10 rappresentazione grafica mediante diagrammi di Eulero-Venn di insieme unione;
la proprietà distributiva.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
DIFFERENZA FRA INSIEMI
L'operazione di differenza fra due insiemi A e B si indica A - B e il risultato è un insieme C i cui elementi sono gli elementi dell'insieme A ad esclusione degli elementi dell'insieme B. Se per esempio l'insieme A è l'insieme di tutti i cittadini italiani mentre l'insieme B è l'insieme di tutti gli uomini e donne la cui altezza è superiore ai 180 cm, allora l'insieme C = A - B è l'insieme di tutti i cittadini italiani ad esclusione di quelli la cui altezza è superiore ai 180 cm ovvero tutti i cittadini italiani la cui altezza è inferiore o uguale a 180 cm. L'insieme D = B - A, invece, è l'insieme di tutti gli uomini e donne la cui altezza è superiore ai 180 cm che "non" sono cittadini italiani. L'operazione differenza di insiemi quindi "non è commutativa", cioè A - B ¹ B - A. Nella rappresentazione grafica di Eulero-Venn gli insiemi differenza sono quelli evidenziati in figura 11.
Fig. 11 rappresentazione grafica di Eulero-Venn di insiemi differenza
L'INSIEME UNIVERSO
Un ruolo chiave nella teoria degli insiemi è il concetto di insieme universo.
Per comprendere che cos'è e come è fatto l'insieme universo dobbiamo fare la seguente considerazione:
quando noi costruiamo un qualsiasi insieme A gli elementi che lo compongono devono necessariamente essere "prelevati" da un insieme più ampio che li contiene.
Per esempio quando noi costruiamo l'insieme P dei numeri pari noi preleviamo questi numeri dall'insieme più ampio N dei numeri interi pari e dispari;
analogamente quando noi costruiamo l'insieme di tutte le auto circolanti con targa Milano noi preleviamo gli elementi di questo insieme dall'insieme di tutte le auto circolanti italiane oppure dall'insieme, ancora più ampio, di tutte le auto circolanti europee.
L'insieme universo, che generalmente si indica con " U ", è l'insieme più ampio con cui noi operiamo e da cui noi preleviamo tutti gli elementi che ci servono per costruire altri insiemi e che, implicitamente o esplicitamente, va sempre specificato.
Ad esempio sia U l'insieme dei numeri interi N e A l'insieme dei multipli di 2;
l'insieme A è: A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ...}.
Sia ora U l'insieme dei numeri interi relativi Z e l'insieme A ancora l'insieme dei multipli di 2.
In questo caso l'insieme A sarà: A = {..., -10, -8, -6, -4, -2, 2, 4, 6, 8, 10, ...} diverso dal precedente.
Quindi è importante, talvolta, specificare in modo esplicito la natura dell'insieme universo, in quanto il cambiamento dell'insieme universo può portare al cambiamento degli insiemi da esso costruiti.
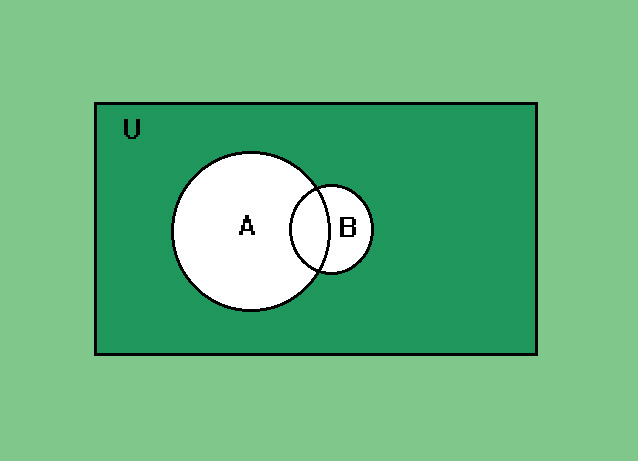
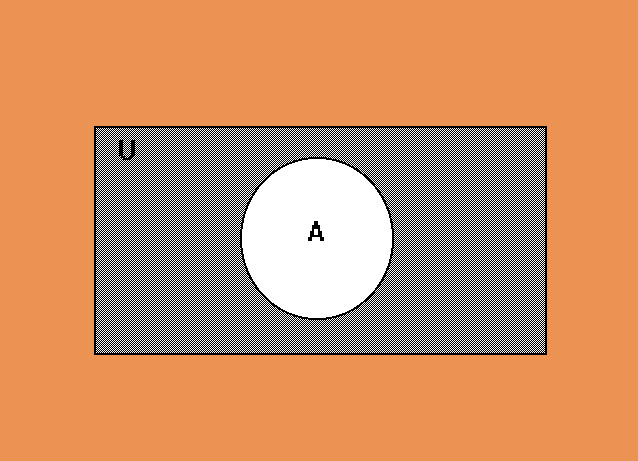
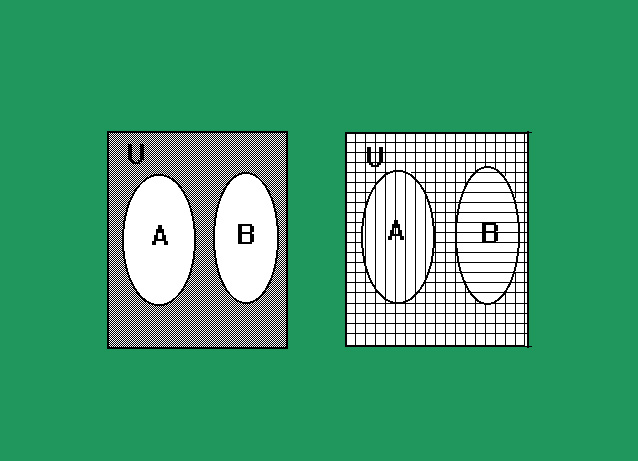
Nella rappresentazione grafica di Eulero-Venn (vedi figura 12) l'insieme universo viene rappresentato con un rettangolo al cui interno ci sono tutti gli insiemi da esso costruiti.
Fig. 12 rappresentazione grafica di Eulero-Venn dell'insieme universo
Dalla definizione data di insieme universo e dalla rappresentazione grafica di Eulero-Venn risulta evidente che:
"ogni insieme A è sempre un sottoinsieme dell'insieme universo U", cioè U U A = U e U Ç A = A.
E' bene far notare che spesso un insieme A può coincidere con l'insieme universo U.
L'INSIEME COMPLEMENTARE
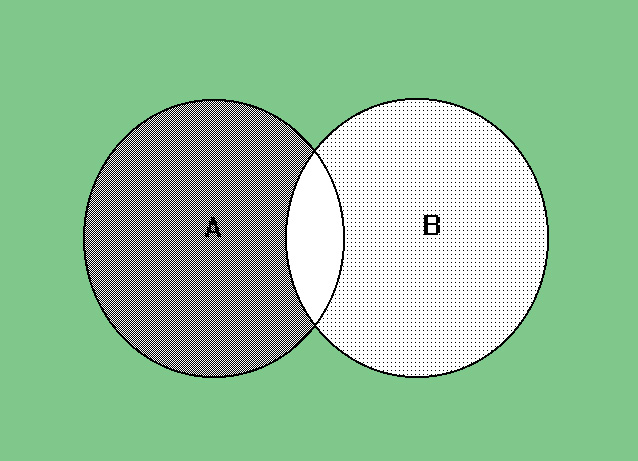
L'insieme complementare, o semplicemente il complementare, di un insieme A rispetto all'insieme universo U viene indicato con A* ed è definito nel seguente modo: A* = U - A. Cioè l'insieme complementare A* è l'insieme di tutti gli elementi che appartengono all'insieme U, ma che non appartengono all'insieme A. Nella rappresentazione grafica di Eulero-Venn (vedi figura 13) l'insieme A* è quello evidenziato in scuro.
Fig. 13 rappresentazione grafica di Eulero-Venn dell'insieme complementare o il complementare
Dalla rappresentazione grafica di Eulero-Venn si vede facilmente che:
A U A* = U
A Ç A* = Æ gli insiemi A e A* sono disgiunti
U U A* = U A* è sottoinsieme di U
U Ç A* = A*
(A*)* = A l'insieme complementare dell'insieme complementare è uguale all'insieme non complementato.
Esistono due notevoli relazioni, note col nome di "Leggi di DeMorgan", che legano le operazioni di unione, intersezione e gli insiemi complementari.
Esse sono:
1. ( A U B )* = A* Ç B*: ovvero il complementare di un insieme ottenuto dall'unione di due o più insiemi è uguale all'insieme ottenuto dall'intersezione dei complementari degli insiemi.
2. ( A Ç B )* = A* U B*: ovvero il complementare di un insieme ottenuto dall'intersezione di due o più insiemi è uguale all'insieme ottenuto dall'unione dei complementari degli insiemi.
Facciamo un esempio:
sia U l'insieme universo U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} e siano
A = {1, 2, 8, 9, 10} e B = {1, 3, 5, 7, 9} due insiemi contenuti in U; vediamo che valgono le due leggi di DeMorgan.
1. L'insieme A U B è l'insieme {1, 2, 3, 5, 7, 8, 9, 10} e il complementare (si intende "sempre" rispetto all'insieme U) di questo insieme è (A U B)* = {4, 6} formato da due elementi. L'insieme complementare di A è A* = {3, 4, 5, 6, 7, 8}, mentre l'insieme complementare di B è B* = {2, 4, 6, 8, 10}; quindi l'insieme intersezione fra A* e B* è A* Ç B* = {4, 6} e la prima legge di DeMorgan risulta verificata.
2. L'insieme A Ç B è l'insieme {1, 9} e il complementare di questo insieme è l'insieme {2, 3, 4, 5, 6, 7, 8, 10}. Ricordando, come visto prima, che da A* = {3, 4, 5, 6, 7, 8} e B* = {2, 4, 6, 8, 10} si ottiene che A* U B* = {2, 3, 4, 5, 6, 7, 8, 10} e quindi anche la seconda legge di DeMorgan risulta verificata.
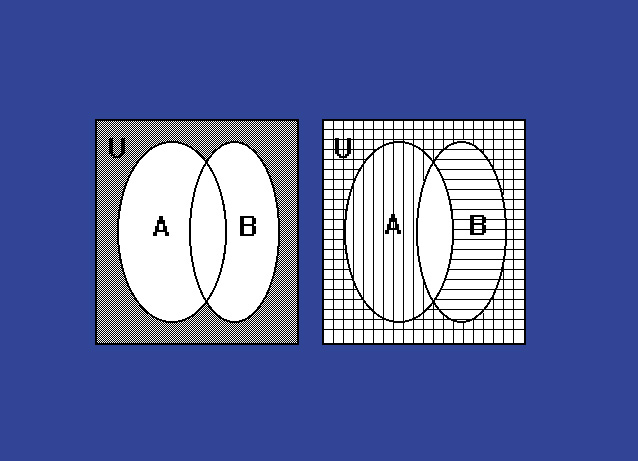
Questa verifica però non è una dimostrazione delle due leggi di DeMorgan in quanto per avere una dimostrazione efficace bisogna mostrare che le due leggi valgono per insiemi qualsiasi. Per fare ciò utilizziamo la rappresentazione grafica di Eulero-Venn procedendo in modo analogo a quanto fatto precedentemente per dimostrare la proprietà distributiva delle operazioni di unione ed intersezione. Lasciando la seconda legge come utile esercizio dimostriamo la prima legge di DeMorgan. Siano A e B due insiemi qualsiasi disgiunti; la rappresentazione grafica di Eulero-Venn dell'insieme (A U B)* è evidenziata in scuro nella parte sinistra della figura 14. L'insieme A* è evidenziato, nelle parte destra della figura 14, con righe orizzontali mentre l'insieme B* è evidenziato con righe verticali. L'insieme A* Ç B* è quell'insieme evidenziato dalle righe orizzontali e verticali. E' evidente che i due insiemi sono uguali.
Fig. 14 rappresentazione grafica di Eulero-Venn sulle proprietà e le operazioni degli insiemi
Per insiemi A e B non necessariamente disgiunti la dimostrazione è del tutto simile e il risultato è visibile nella figura 15.
Fig. 15 rappresentazione grafica di Eulero-Venn insiemi non necessariamente disgiunti
PRODOTTO CARTESIANO FRA DUE INSIEMI
Le operazioni fra insiemi che abbiamo visto associano a due o più insiemi un terzo insieme formato dagli elementi degli insiemi A, B, C, ecc. che possono essere tutti gli elementi - unione -, gli elementi in comune - intersezione -, e via dicendo.Fondamentale è il fatto che da insiemi numerici, per esempio, si ottengono insiemi ancora numerici.
In sostanza la natura degli elementi che compongono l'insieme risultante non viene mutata dalle operazioni che abbiamo visto.
Il prodotto cartesiano fra due insiemi, invece, associa a due insiemi A e B un insieme C i cui elementi sono "coppie ordinate degli elementi dell'insieme A e dell'insieme B".
Coppia significa che ogni elemento dell'insieme C è della forma (a, b), dove a appartiene all'insieme A e b appartiene all'insieme B;
ordinata vuol dire che la coppia (a, b) è diversa dalla coppia (b, a).
L'insieme prodotto cartesiano fra gli insiemi A e B si indica A x B. Per esempio se A è l'insieme {1, 2, 3} e B è l'insieme {1, 2}, allora l'insieme prodotto cartesiano è A x B = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 1), (3, 2)}.
Se l'insieme A ha n elementi e l'insieme B ha m elementi l'insieme A x B ha n x m elementi.
Nell'esempio precedente l'insieme A ha 3 elementi, l'insieme B ha 2 elementi e l'insieme A x B ha 3 x 2 = 6 elementi (coppie ordinate).
Se facciamo il prodotto cartesiano B x A otteniamo l'insieme {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3)} il quale è diverso dall'insieme A x B dato che in A x B sono presenti le coppie (3, 1) e (3, 2) che nell'insieme B x A mancano.
L'insieme A x B è quindi diverso dall'insieme B x A, non vale cioè la proprietà commutativa.
L'insieme prodotto cartesiano ha una utilissima rappresentazione grafica:
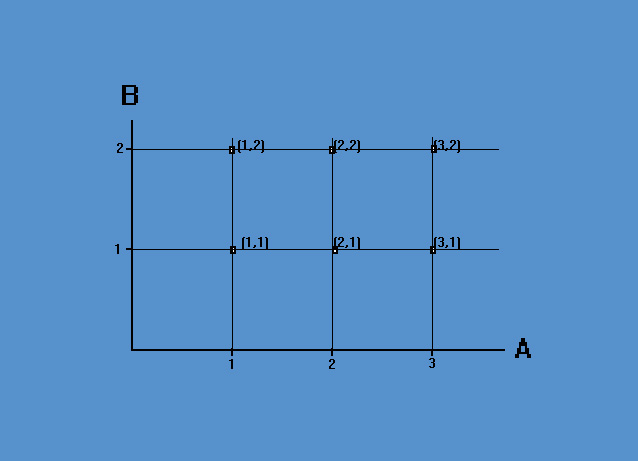
se sistemiamo gli elementi del primo insieme A del prodotto su una retta orizzontale, mentre gli elementi del secondo insieme B del prodotto su una retta verticale perpendicolare all'altra, allora gli elementi dell'insieme prodotto cartesiano A x B sono i punti del piano dove si intersecano le rette passanti per gli elementi dei due insiemi A e B e parallele alle due rette contenenti gli elementi degli insiemi A e B (vedi figura 16).
Uno dei più importanti insiemi prodotto cartesiano è l'insieme dei numeri complessi C = R x I, dove R è l'insieme dei numeri reali mentre I è l'insieme dei numeri immaginari.
Fig. 16 rappresentazione grafica su diagramma cartesiano del prodotto di insiemi
![]()
![]()
INSIEME DELLE PARTI O INSIEME POTENZA
Dato un insieme A si considerino tutti i sui sottoinsiemi; l'insieme di tutti i sottoinsiemi di un insieme A si chiama "insieme delle parti di A" e si indica con P(A). Se per esempio l'insieme A è l'insieme {1, 2, 3}, i suoi sottoinsiemi sono: Æ, A (ricordiamoci che sia l'insieme vuoto che l'insieme A sono sottoinsiemi di A), {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. L'insieme delle parti è quindi: P(A) = {Æ, A, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}}. Se l'insieme A ha n elementi, l'insieme P(A) ha 23 elementi; nell'esempio precedente l'insieme A ha 3 elementi e quindi l'insieme delle parti ha 8 elementi. E' possibile poi costruire l'insieme delle parti delle parti di A, che si indica con P2(A), cioè l'insieme di tutti i sottoinsiemi dell'insieme P(A); continuando questo procedimento si possono ottenere insiemi con un numero molto grande di elementi partendo da insiemi con un numero limitato di elementi.Gli insiemi Z e Q
I numeri naturali preceduti dal segno + formano l'insieme dei numeri interi positivi che si indica con Z+, quelli preceduti dal segno - formano l'insieme dei numeri inte ri negativi che si indica con Z-.
I due insiemi Z+ e Z- formano complessivamente l'insieme dei numeri interi che si indica con Z.
I numeri razionali preceduti dal segno + formano l'insieme dei numeri razionali positivi che si indica con Q+, quelli preceduti dal segno - formano l'insieme dei nume ri razionali negativi che si indica con Q-.
I due insiemi Q+ e Q- formano complessivamente l'insieme dei numeri razionali re lativi che si indica con Q.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()