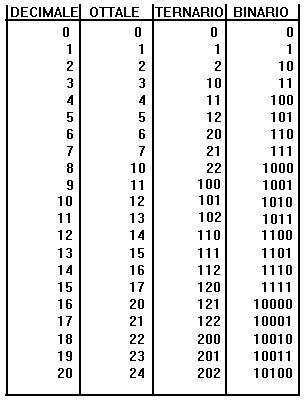
Tabella: valori numerici da 0 a 20
Conversione del numero 141 al suo numero binario
Conversione del numero 1299 al suo numero binario
![]()
![]()
Dal web la numerazione:
Youmath Sistemi di numerazione
Informatica abaluth Il computer Le informazioni Sistemi di numerazione
Uni Roma PASCAL Sistemi Numerazione presentazione
Matematicamente Sistemi numerazione
Youtube Video Sistemi di numerazione
Express Adobe La Storia dei Sistemi di numerazione
Matematica Read the docs I sistemi di numerazione
Wiki books Fondamenti di informatica Sistemi di numerazione
Staff Polito Sistemi di numerazione
Liceo Medi Senigallia Approfondimenti Sistemi di numerazione
Banorri Altervista I sistemi di numerazione
Slide serve Sistemi di numerazione
Monte Europe Il sistema di numerazione
Scarabeo kheper Altervista Sistemi di numerazione
Knowledge Center Altervista Elettronica digitale Logica di base
Corso Php Mysql Altervista Wordpress Sistemi di numerazione
Mauitaui Sistema di nuemrazione Binario
Microsoft Convertire i numeri in sistemi di numerazione differenti
Uni Na Calcolatori Biomedica Sistemi numerazione
Campus Hubscuola Il sistema di numerazione
Giunti Scuola Antichi sistemi di numerazione
Uccellani Sistemi di numerazione
Liceo Cuneo Sistemi di numerazione
![]()
![]()
MATEMATICA - SISTEMI DI NUMERAZIONE
Sappiamo tutti cosa indica il numero 1580 e sappiamo anche che esso è diverso dal numero 8051 nonostante sia formato con le stesse cifre del numero precedente.
In matematica succede che un numero possa avere valori diversi in relazione al sistema numerico adottato:
per esempio il numero 10 vale 10 nel sistema decimale;
2 nel sistema binario e 8 nel sistema ottale.
Il sistema di numerazione con cui siamo abituati a lavorare prende il nome di "sistema numerico posizionale decimale", o a base 10, in quanto i numeri si ottengono mediante una composizione delle 10 cifre 0, 1, 2, 3, ..., 9 in cui la posizione della cifra rispetto alla prima partendo da destra indica l'esponente della base 10 (decimale appunto) che moltiplica la cifra.
La posizione delle cifre che compongono il numero è fondamentale, infatti il numero 129 è diverso dal numero 921 ottenuto scombinando la prima cifra con l'ultima.
Quando scriviamo o leggiamo il numero 2327 implicitamente noi intendiamo 2 migliaia, cioè 2 x 103 , 3 centinaia, cioè 3 x 102 , 2 decine, ovvero 2 x 101 e 7 unità, cioè 7 x 100 (ricordiamoci che qualsiasi numero elevato allo zero vale 1);
il numero 2327 è quindi 2 x 103 + 3 x 102 + 2 x 101 + 7 x 100 .
Analogamente 47081 = 4 x 104 + 7 x 103 + 0 x 102 + 8 x 101 + 1 x 100 .
Questa rappresentazione di un numero come somme di potenze di 10 prende il nome di "sviluppo a base 10".
Il sistema numerico a base 10 non è l'unico possibile, esistono infatti sistemi di numerazione a base 8 (ottale), a base 12 (duo-decimale), a base 16 (esadecimale), a base 3 (ternario) e, attualmente il più diffuso, a base 2 (binario).
Tabella: valori numerici da 0 a 20
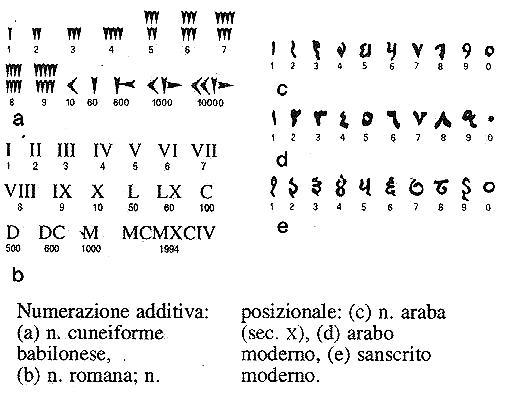
La matematica degli antichi Babilonesi si basava su un sistema numerico a base 60, cioè un'unità formata da 60 sottounità, ed è ancora oggi in vigore nella suddivisione delle ore in minuti e dei minuti in secondi (poi si passa al sistema decimale con i decimi di secondo, i centesimi di secondo, ecc.) e nella suddivisione degli angoli.
Per i Babilonesi questo sistema era molto comodo perché permetteva di dividere facilmente una unità in due parte (30 sottounità), in tre parti (20 sottounità), in 4 parti (15 sottounità), in 5 parti (12 sottounità), in 6 parti (10 sottounità), in 10 parti (6 sottounità), in 12 parti (5 sottounità), in 15 parti (4 sottounità), in 20 parti (3 sottounità) e in 30 parti (2 sottounità).
La comodità di questo sistema numerico gli ha permesso di sopravvivere fino ai giorni nostri.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
SISTEMA BINARIO
Il sistema binario è attualmente il più diffuso in quanto tutte le calcolatrici elettroniche, i computer, le logiche di controllo e in generale tutti i circuiti digitali utilizzano il sistema binario.Si tratta di un sistema molto comodo e semplice.
Le cifre nel sistema numerico binario sono due: lo "0" e l'"1";
è posizionale e la base è 2;
questo vuol dire che, per esempio, il numero binario 101101 (si legge: uno, zero, uno, uno, zero, uno, e non centounomilacentouno) ha un valore numerico decimale pari a:
101101 = 1 x 25 + 0 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 32 + 8 + 4 + 1 = 45
Le apparecchiature elettroniche come i computer utilizzano il sistema binario (chiamato in queste applicazioni sistema digitale, cioè a due valori) perché per un circuito logico di trasmissione, elaborazione e memorizzazione dei dati il modo più conveniente e affetto dal minor numero possibile di errori è considerare due stati del circuito:
acceso, stato di ON equivalente a "1", e spento, stato di OFF equivalente a "0".
Per convertire un numero in notazione binaria in un numero decimale si procede nel seguente modo:
1) si contano le cifre del numero binario e si sottrae 1 (esempio: 1010 ha 4 cifre, meno 1 otteniamo 3)
2) il numero così ottenuto è l'esponente maggiore delle sviluppo a base due
3) le potenze successive nello sviluppo sono decrescenti e il coefficiente che moltiplica la base è relativo alla posizione della cifra binaria:
per il numero 1010 la prima cifra (da sinistra) è 1 e va moltiplicata per la base elevata all'esponente massimo;
quindi 1 x 23 .
La seconda cifra è 0 e va moltiplicata per la base elevata all'esponente massimo meno uno (3 - 1 = 2);
quindi 0 x 22 .
La terza cifra è 1 che va moltiplicata per la base elevata all'esponente massimo meno due (3 - 2 = 1);
quindi 1 x 21 .
La quarta e ultima cifra è 0 e va moltiplicata per la base elevata all'esponente massimo meno tre (3 - 3 = 0);
quindi 0 x 20 .
Quando si arriva all'ultima cifra del numero binario l'esponente della base deve essere sempre uguale a zero altrimenti abbiamo commesso qualche errore.
Come utile esercizio si provi a convertire in numero decimale il numero binario 10101011.
La conversione di un numero decimale nel suo corrispondente binario è un po' più laboriosa e conviene procedere nel seguente modo:
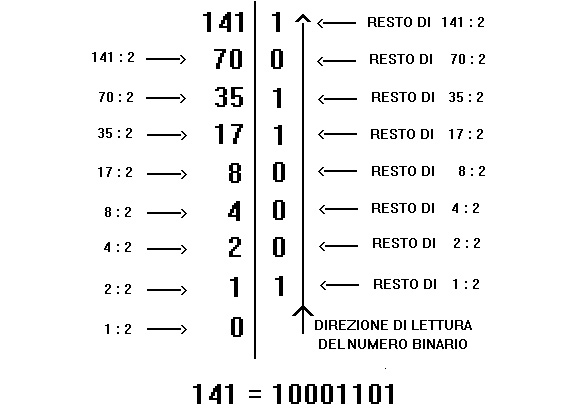
con riferimento alla tavola 1, per convertire in numero binario il numero decimale 141 tracciamo una riga verticale ed eseguiamo la divisione intera di 141 diviso 2.
Il risultato, 70, viene scritto sotto 141 mentre il resto, in questo caso 1, viene scritto di fianco a 141.
Dividiamo ora 70 per 2;
il risultato, 35, viene scritto sotto 70 e il resto della divisione, in questo caso 0, viene scritto di fianco a 70.
Continuando questa procedura arriveremo all'ultimo passaggio che sarà la divisione di 1 per 2 che ha come risultato 0 e resto 1.
Il numero binario corrispondente al numero decimale 141 sono tutti i resti delle divisioni successive e si legge dal basso verso l'alto.
Come ulteriore esempio, in tabella 2 è riportata la conversione dal numero decimale 1299 al suo corrispondente numero binario.
Conversione del numero 141 al suo numero binario

Conversione del numero 1299 al suo numero binario
La somma e il prodotto di due numeri binari sono molto semplici da effettuare e, sostanzialmente, si eseguono come per gli ordinari numeri decimali;
l'unica differenza di cui bisogna tener conto è che 1 + 1 in binario fa 10, cioè 1 con riporto di 0.
Se vogliamo, per esempio, sommare i due numeri binari 1101 (11 in decimale) e 110 (6 in decimale) incolonniamo i numeri allineandoli a destra (come per la somma decimale):
1011 +
110 =
--------
partendo da destra 1 + 0 = 1 riporto 0, quindi di scrive 1 sotto la colonna di
cifre di destra:
1011 +
110 =
-------
1
la somma successiva è 1 + 1 = 0 con riporto di 1, quindi si scrive 0 e il
riporto si sommerà nel seguente passaggio:
1011 +
110 =
-------
01
la somma successiva è 0 + 1 = 1 e sommando il riporto otteniamo 1 + 1 = 0 con
riporto 1;quindi si scrive 0 e si riporta 1
1011 +
110 =
-------
001
Ultimo passaggio: si somma 1 del primo numero binario con il riporto della somma
precedente e otteniamo 1 + 1 = 10 (questa volta è inutile utilizzare il
riporto), quindi:
1011 +
110 =
---------
10001
Il risultato della somma è 10001 che convertito in decimale fa 17 come doveva
essere poiché 1011 = 11 e 110 = 6.Il prodotto fra due numeri binari si riduce essenzialmente a una somma, infatti se vogliamo eseguire il prodotto fra i due numeri binari 1011 e 110 incolonniamo i numeri come fatto per la somma e facciamo il prodotto a termine come nell'usuale prodotto decimale:
la prima riga che otteniamo sono tutti zeri dato che 1 ¦ 0 = 0 e 0 ¦ 0 = 0
1011 *
110 =
---------
0000
la seconda riga invece è 1011 perché tutte le cifre sono moltiplicate per 1
quindi:
1011 *
110 =
----------
0000
1011-
e analogamente per la terza riga otteniamo:
1011 *
110 =
----------
0000
1011-
1011--
Ora si tratta solo di eseguire la somma dei numeri binari 10110 e 101100 che
lasciamo come esercizio.Come avrete certamente capito il prodotto fra due numeri binari si realizza riscrivendo il primo fattore moltiplicativo ogni volta che nel secondo fattore moltiplicativo c'è un "1".
Ad esempio 1100101 ¦ 1111 si incolonna per la somma nel seguente modo:
1100101 *
1111 =
------------
1100101
1100101-
1100101--
1100101---
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()
