Matematica Aritmetica Geometria Matematica Geometria Piana e Solida Informatica Media
MATEMATICA - LA PROPORZIONALITA'
I RAPPORTI
In un precedente capitolo abbiamo già parlato di rapporti fra numeri, le frazioni. Vogliamo ora riprendere l'argomento per approfondirlo e, soprattutto, per cercare di coglierne le possibili applicazioni, estendendone lo studio ai rapporti tra misure di grandezze. Ti renderai conto di come svariate questioni pratiche e un lunghissima serie di fenomeni naturali possano essere studiati ricercando un legame preciso tra le grandezze che intervengono nel fenomeno e unificati in un unico tipo di problema: la proporzionalità. Alcuni esempi serviranno a chiarire quanto sia ricco di significato il concetto di rapporto. Non so se tu sia un appassionato di ciclismo, ma, senza dubbio, avrai sentito parlare di Fausto Coppi, forse il più famoso ciclista che sia mai esistito. Nel 1952 il grande atleta percorse i 3.964 km del Giro d'Italia a una velocità media di 34,560 km/h (leggi: «chilometri all'ora»): una media notevole per quei tempi, soprattutto se si considera l'elevato numero di tappe alpine e appenniniche. Forse ti chiederai se, conoscendo la velocità media, sia possibile calcolare quanto tempo impiegò complessivamente Fausto Coppi per percorrere tutti i 3.964 km del Giro. Vedremo che problemi di questo genere sono facilmente risolubili. Consideriamo ora un altro esempio: la propagazione del suono. Il suono si propaga nell'aria a una velocità di 340 m/sec (leggi: «metri al secondo»), nei corpi solidi a una velocità di circa 3.880 m/sec (noterai che 3.880 è circa 10 volte maggiore di 340), nell'acqua, infine, a una velocità di 1.500 m/sec. Intuirai facilmente che un pescatore subacqueo sentirà il suono di una campana agitata a fior d'acqua prima di un villeggiante che, sulla sua barca, si trovi lontano dalla fonte sonora tanto quanto il pescatore. Avrai già capito anche il motivo per cui gli Indiani appoggiavano l'orecchio a terra per sentire, anche a grande distanza. l'arrivo di un treno o di una mandria di bufali. Fermiamoci per ora e cerchiamo di fare alcune considerazioni. Negli esempi riportati si parla di velocità. La velocità di un corpo o, nel caso del suono, di onde, si esprime tramite il rapporto tra la misura dello spazio percorso e il tempo impiegato a percorrerlo. Scriveremo: v = s/t, dove s indica lo spazio percorso e si misura in metri o in multipli e sottomultipli del metro, mentre t è il tempo e si misura in secondi o in altre unità di tempo. Ora, questo rapporto può rimanere costante nel tempo, come nel caso di propagazione di onde sonore rispettivamente nell'aria, nell'acqua, nei solidi, oppure subire variazioni, come nel caso di un ciclista che ripercorre il medesimo tratto. Tutti noi d'altra parte sappiamo che la stessa via può essere percorsa in automobile in tempi più o me a seconda dell'intensità del traffico. Vi sono quindi rapporti variabili e altri che non mutano, hanno cioè valore costante.![]()
![]()
Ti sarà facile individuare nei seguenti esempi i rapporti del primo e del secondo del tipo: a) rapporto tra la distanza massima (270 milioni di km) e la distanza minima (56 milioni di km) del pianeta Marte dalla Terra; b) rapporto tra il lato di un triangolo equilatero e il p del triangolo stesso; c) rapporto tra il valore della lira e il valore del dollaro in tempi diversi: d) rapporto tra il numero dei giocatori di una squadra di calcio e il numero dei giocatori squadra di pallacanestro; e) rapporto tra lo spazio e il tempo impiegato a percorrerlo (velocità). Noterai che negli esempi fatti finora compaiono sia rapporti fra numeri, sia rapporti tra grandezze che possono essere della stessa specie (e si riferiscono quindi alla stessa unità di misura) o di specie diversa. Siano allora rispettivamente a e b le misure di due grandezze A e B e r il loro rapporto. Noterai che il rapporto r = a/b potrà essere a sua volta una misura o un numero puro, a seconda che le due grandezze siano di specie diversa (ad es. spazio e tempo) o della stessa specie. Gli esempi che seguono serviranno a chiarire meglio questo concetto. Senza dubbio sai che in una squadra di calcio per ogni portiere vi sono due terzini. Il rapporto tra portiere e terzini è sempre 1/2, e senz'altro, essendo un rapporto fra numeri, è esso stesso un numero. Considera ora rapporto che non sia fra numeri, ma fra grandezze. Saprai già che un corpo sulla Luna è meno pesante che sulla Terra, data la differente forza di gravità. Infatti, la forza di gravità sulla Luna è 1/6 della forza di gravità sulla Terra. Un uomo dal peso di 72 kg peserebbe sulla Luna solo 72/6 = 12 kg. Possiamo scrivere che il rapporto tra il peso dell'uomo rispettivamente sulla Luna e sulla Terra sarà dato da:
12 kg.
r = ------ = 1/6.
72 kg.
In questo caso, il rapporto tra misure di grandezze della stessa specie (nota che non si tratta di un rapporto fra numeri, ma tra pesi espressi in chilogrammi) porta ancora a un numero puro, e il valore di r ci dice soltanto che il peso di un uomo (o di un sasso o di un modulo spaziale o di qualsiasi altro corpo) sulla Luna è sempre 6 volte minore del peso dello stesso uomo sulla Terra, di qualsiasi peso si tratti, e che, viceversa, il suo peso sulla Terra è sempre 6 volte maggiore di quello che avrebbe sulla Luna.
Avrai certamente capito che, per ognuno dei precedenti rapporti, è sempre possibile determinare il reciproco (o rapporto inverso): infatti, se il rapporto tra portiere e terzini è 1/2, il rapporto tra terzini e portiere è 2/1 = 2. Si avrà quindi che, se r = a/b, sarà anche 1/r = b/a. Inoltre, la notazione r = a/b ci permette di rilevare che:
Conoscendo r e a, è possibile determinare b = a/r; e conoscendo r e b, è possibile determinare a = r¦b.
Un altro esempio ti permetterà di comprendere meglio le possibilità di applicazione di questi ultimi concetti. In una gara automobilistica di regolarità non è tanto indispensabile essere veloci, quanto rispettare alcune tabelle di marcia, per esempio, percorrere 180 Km di strada normale magari con alcuni tratti di montagna, mantenendo una media di 90 km/h. Se il pilota è molto bravo e non commette errori, in quanto tempo dovrebbe percorrere i 180 Km?
![]()
![]()
180 km
t = -------- = 2 h.
90 km/h
Con questo esempio puoi anche verificare quanto già è stato detto, cioè che, quando in un rapporto compaiono grandezze che non sono della stessa specie, il risultato non è un numero puro, ma è esso stesso la misura di una certa grandezza: nel nostro caso si tratta del tempo che il pilota dovrebbe impiegare per portare «regolarmente» a termine la gara.
PROPORZIONI
Ti sei mai posto il problema di disegnare su un foglio lo schema di un campo da football (ovviamente rimpicciolendolo, ma conservando i rapporti tra le varie dimensioni? Sai già che un campo da gioco regolamentare ha forma rettangolare e che le lunghezze dei lati variano da un minimo di 45 m a un massimo di 90 per il lato minore e da un minimo di 90 a un massimo di 120 m per il lato maggiore. Consideriamo per semplicità il campo i cui lati, minore e maggiore (indichiamoli con le lettere a e b), siano lunghi rispettivamente 90 e 120 metri e rappresentiamolo come un rettangolo i cui lati c e d siano rispettivamente 9 e 12 cm.Il campo reale e il rettangolo disegnato avranno forma uguale ma, ovviamente, dimensioni diverse. Noterai però che i valori dei rapporti a/b e c/d sono uguali. Infatti
90 m
a/b = -------
120 m
è un numero puro uguale a 3/4 (ricorda le proprietà delle frazioni) e,
analogamente
9 cm
c/d = ------ = 3/4.
12 cm
E' chiaro allora che il mantenimento della forma non è caratterizzato da
un numero, ma piuttosto dall'uguaglianza di rapporti fra numeri o, in altri
termini, da proporzioni. Possiamo dire che il campo reale e la sua
rappresentazione grafica sono figure simili.Cos'è allora una proporzione? Non è altro che un'uguaglianza di rapporti e si può indicare con la notazione a/b = c/d oppure sotto la forma a:b = c:d, che si legge: «a sta a b come c sta a d»
I termini a e d vengono chiamati estremi, mentre i termini b e c sono detti medi. Il primo e i terzo termine sono detti anche antecedenti, e il secondo e il quarto conseguenti. Consideriamo ora il nostro rettangolo di dimensioni 9 e 12 cm e un altro di lati, rispettivamente, di 3 e 4 cm, disponendo i rettangoli come in figura 68.
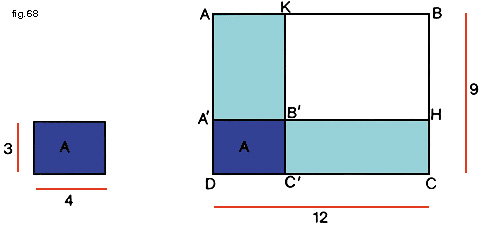
Scriveremo che 3:4= 9:12 e diremo che l'altezza del rettangolo A sta alla base di A, come l'altezza del rettangolo B sta alla base di B. Nota che anche il rettangolo di dimensioni 3 e 4 cm ha la stessa forma del nostro campo da gioco. Ma torniamo alla figura 68. E' facile verificare che l'area del rettangolo AKC'D è uguale all'area del rettangolo A'HCD. Infatti, l'area del primo rettangolo è data da 9 cmx4 cm = 36 cm2e l'area del secondo è data da 12 cmx3 cm = 36 cm2.
L'esempio geometrico ci permette di dedurre la proprietà fondamentale delle proporzioni:
In una proporzione il prodotto dei medi è uguale al prodotto degli estremi.
Nel nostro caso 3 e 12 sono gli estremi e 4 e 9 sono i medi. Possiamo allora dire che, per ogni generica proporzione a:b = c:d, si ha che axd = bxc. Ovviamente vale anche la proprietà inversa e cioè:
dati quattro numeri a, b, c, d tali che axd sia uguale a bxc, allora si avrà anche che a:b = c:d.
Considera ad esempio un onda sonora che, nell'aria, percorre 340 m in un secondo e 1020 m in 3 secondi. Ti chiederai se i numeri 340,1,1.020,3 formino, nell'ordine in cui sono stati presi, una proporzione. Ora, essendo 340x3 = 10201, possiamo senz'altro rispondere affermativamente e scrivere che 340:1 = 1020:3. Ma torniamo al nostro esempio geometrico. Abbiamo visto come, dall'osservazione dei due rettangoli simili A e B, siamo arrivati a scrivere la proporzione 3:4 = 9:12 (1). D'altra parte, potrai tu stesso verificare, effettuando una rotazione di ciascun rettangolo in modo che la base diventi l'altezza, che è possibile scrivere anche la seguente proporzione: 4:3 = 12:9 (2). A questo punto avrai già capito che, essendo una proporzione un'uguaglianza di rapporti, allora potremo scrivere anche che 3:9 = 4:12 (3) e questa scrittura, dal punto di vista geometrico, significa che l'altezza del rettangolo A sta all'altezza del rettangolo B come la base di A sta alla base di B. Osserva che quest'ultima proporzione si ottiene dalla prima permutando i medi. Potremmo pensare di permutare gli estremi invece dei medi: otterremo in tal caso la nuova proporzione 12:4 = 9:3 (4). Dal punto di vista geometrico la (4) significa: la base del rettangolo B sta alla base del rettangolo A come l'altezza di B sta all'altezza di A. Ti sarai già reso conto che, tanto nella proporzione (2) quanto nelle (3) e (4), è sempre rispettata la proprietà fondamentale delle proporzioni.
In generale, data una generica proporzione a:b = c:d, è sempre possibile:a) invertire ogni antecedente con il proprio conseguente
b) scambiare di posto (permutare) i medi tra loro o gli estremi tra loro.
Quindi si può scrivere che, se a:b = c:d, allora si ha anche: b:a = d:c, e a:c = b:d e d:b = c:a.
Un esercizio che sembra quasi un gioco: prova a scrivere tutte le proporzioni che si possono ottenere dalla nostra proporzione originale 3:4 = 9:12, invertendo e permutando tutte le volte che vuoi, ma badando che, in tutte le proporzioni che scriverai, il prodotto dei medi sia sempre uguale al prodotto degli estremi e cioè uguale a 36. Verificherai che si può operare sui quattro termini di una proporzione in qualunque modo, purché sia sempre rispettata la proprietà fondamentale.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
RISOLUZIONE DI PROBLEMI PER MEZZO DI PROPORZIONI. PROPORZIONALITA' DIRETTA E INVERSA
Abbiamo visto come una proporzione non sia altro che un'uguaglianza di rapporti. La proprietà fondamentale delle proporzioni ti permetterà di determinare un termine incognito in una proporzione. Supponiamo di voler determinare, per esempio, il numero x tale che sia in proporzione con i numeri 4, 6, 12 presi nell'ordine dato, tale cioè che 4:6 = 12:x.In base alla proprietà fondamentale si ha: 4xx = 6x12 e quindi 4x = 72, da cui si ricava x = 72/4 = 18. Vediamo insieme un altro esempio numerico. Calcoliamo il valore di y nella proporzione 5: 7/3 = y:14. Dovrà essere 5x14 = 7/3xy e quindi 70 = 7/3xy cioè y = 70x3/7 = 30.
Verifica tu stesso che i valori x = 18 e y = 30 soddisfino le proporzioni date.
Negli esempi riportati ti si chiedeva unicamente di determinare il termine incognito basandoti sulla proprietà fondamentale delle proporzioni. Ma per risolvere un problema bisogna che tu sappia individuare non solo il termine incognito, bensì anche il tipo di legame (di proporzionalità) esistente tra i dati che ti vengono forniti. Cerchiamo allora di fare alcuni esempi concreti che permettono di comprendere meglio il concetto di proporzione e la sua applicabilità. In molti casi, infatti, il legame tra le grandezze che intervengono in un fenomeno è una legge di proporzionalità diretta o inversa. Ti chiederai cosa significhi dire che due grandezze sono direttamente o inversamente proporzionali. Vediamolo, come è ormai nostra abitudine, con alcuni esempi.
Supponi di appendere a un elastico, fissato a un supporto rigido, via via dei pesi diversi. L'allungamento dell'elastico sarà tanto maggiore, quanto più pesante è il corpo a esso appeso.
Un altro esempio è il rapporto tra l'intensità dello sforzo fisico di un sollevatore di pesi, e il peso da sollevare:
lo sforzo sarà tanto maggiore quanto maggiore è il peso.
Nell'esempio precedente abbiamo rilevato gli allungamenti misurati ed espressi in centimetri, subiti dall'elastico in corrispondenza dei vari pesi espressi in grammi. Ti chiederai forse quale sia il legame esistente tra le misure dei pesi applicati e le misure dei corrispondenti allungamenti. Osservando i dati rilevati, è facile verificare che:
0,5 = 50x0,01, 1,5 = 150x0,01, 3 = 300x0,01, e anche che il rapporto tra le coppie di valori 0,5 e 50, 1,5 e 150,... è costante e uguale a 0,01.
E ricordando che una proporzione non è altro che una uguaglianza di rapporti, potremo certamente scrivere:
0,5:50 = 1,5:150, ecc.
Possiamo inoltre affermare che, se conosciamo il peso applicato, è possibile risalire al corrispondente allungamento subito dall'elastico semplicemente moltiplicando il peso espresso in grammi per il valore della costante che, nel nostro caso, è 0,01. In altri termini, è sufficiente stabilire una proporzione nella quale l'entità dell'allungamento compaia come incognita. Vogliamo, per esempio, calcolare l'allungamento y che si ha per un peso di 500 g. Basta scrivere: 50:0,5 = 500:y e ricavare y = 500x0,5:50 = 500x0,01 = 5.
Ed è possibile, conoscendo viceversa l'entità dell'allungamento, calcolare il valore del peso che l'ha provocato? Certamente: scriveremo in questo caso una proporzione nella quale il termine incognito sia il peso, per esempio: 300:3 = x:4; potremo ricavare x = 4x300/3 = 400.
Se indichiamo con la lettera a i pesi e con b i corrispondenti allungamenti, possiamo senz'altro scrivere che b = kxa, dove k è una costante che, nel nostro caso, assume il valore di 0,01. E potremo anche scrivere che a = b/k (x = 4/0,01). Diciamo, per concludere, che tra pesi e allungamenti esiste una proporzionalità diretta di coefficiente 0,01.
Parlando in generale:
Si ha proporzionalità diretta tra due serie di valori qualsiasi a e b, tutte le volte che, per ogni valore di a, vale la relazione b = kxa, dove k è una costante; quindi il rapporto tra a e b è costante: b/a = k.
Passiamo ora alla proporzionalità inversa. Ti è mai capitato di pizzicare le corde di una chitarra e sentire la diversità delle note che si ottengono spostando il dito sulla tastiera? Ora, quando si fa vibrare una corda (per esempio, appunto, le corde di una chitarra; ma il discorso vale per qualsiasi altro strumento musicale a corda), questa produce un suono più o meno alto (note diverse) a seconda che il numero di vibrazioni per minuto secondo sia più o meno elevato. Si verifica che, se una corda produce un certo numero di vibrazioni al secondo, la metà della corda produce un numero doppio di vibrazioni al secondo, 1/3 della corda produce un numero triplo di vibrazioni, e così via. Ti sarà chiaro ora perché, per ottenere note diverse pizzicando la corda di una chitarra, si fa variare la lunghezza della corda stessa spostando il dito sulla tastiera che, avrai senz'altro notato, è divisa in un certo numero di settori da strisce metalliche rilevate.
Nella tabella sottostante riportiamo le diverse lunghezze di una corda e il corrispondente numero di vibrazioni al secondo. Anche in questo caso, come già abbiamo fatto per la proporzionalità diretta, chiediamoci qual è il legame esistente tra i valori riportati nelle due colonne. Puoi facilmente verificare che 60x400 = 24.000, 30x800 = 24.000, 20x1200 = 24.000... Per estensione, possiamo dire che anche xx1.600 = 24.000 e quindi x = 24.000/1.600 = 15, e che 10xy = 24.000 e quindi y = 24.000/10 = 2.400. Se indichiamo con a e b rispettivamente le lunghezze della corda e le corrispondenti vibrazioni al secondo, possiamo senz'altro scrivere che axb = k (quindi a = k/b e b = k/a), tenendo presente che, nel nostro esempio, k è uguale a 24.000. In generale possiamo dire che:
Si ha proporzionalità inversa tra due serie qualsiasi di valori a e b, tutte le volte che, per ogni valore di a, b assume il valore k/a (e, viceversa, per ogni valore di b, a assume il valore k/b) o, in altri termini, il prodotto axb = k, dove k è una costante.
¦
Press. ¦ T ebolliz.
-----------+-----------
1 ¦ 100°
¦
0,692 ¦ 90°
¦
0,467 ¦ 80°
¦
0,122 ¦ 50°
¦
Tornando al nostro esempio e ricordando la proprietà fondamentale delle proporzioni, avendo verificato che:
60x400 = 30x80 = ... = xx1.600 = yx10 = 24.000
ci sarà possibile scrivere una proporzione nella quale due qualsiasi coppie di fattori compaiono indifferentemente l'una come estremi e l'altra come medi: considerando per esempio le due coppie 30 e 800, x e 1.600, scriveremo:
30:x = 1.600:800.
Riassumendo, possiamo dire che:
Due grandezze sono direttamente proporzionali quando variano in modo tale che, se una raddoppia, triplica, ecc., anche l'altra raddoppia, triplica, ecc.; sono invece inversamente proporzionali quando variano in modo tale che, se una grandezza raddoppia, triplica, ecc., l'altra diventa la metà, un terzo, ecc., della prima.
Considera ora il seguente esempio e verifichiamo insieme se esiste un legame di proporzionalità (diretta o inversa) o no tra le grandezze in gioco nel fenomeno illustrato. Ti sei mai chiesto per quale motivo l'acqua bolla a una temperatura inferiore a 100°C in alta montagna? Oppure perché la sterilizzazione degli strumenti chirurgici avviene in autoclave, in un ambiente, cioè, in cui la pressione è maggiore della pressione atmosferica sul livello del mare? La temperatura di ebollizione di un liquido (l'acqua, per esempio) dipende dalla pressione esercitata dalla colonna d'aria sulla superficie del liquido: aumenta con l'aumentare della pressione e, ovviamente, diminuisce con il diminuire della pressione.
Indichiamo con I la pressione al livello del mare e vediamo come varia la temperatura di ebollizione dell'acqua al variare della pressione (vedi tabella sopra riportata). Dato che, al diminuire della pressione, anche la temperatura di ebollizione diminuisce, possiamo escludere la proporzionalità inversa. Ma ci troviamo davvero di fronte a un caso di proporzionalità diretta Ricordiamo che, perché ci sia proporzionalità diretta, il rapporto tra le coppie di valori pressione temperatura deve essere costante. Ma è facile verificare che 1/100 è diverso da 0,692/90. diverso da 0,467/80 e così via. Quindi pressione e temperatura non sono né direttamente né inversamente proporzionali.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()
