![]()
Yahoo! Video I numeri razionali
YouTube I Numeri Razionali Rai Scuola Cultura
I Numeri complessi I Numeri Immaginari I numeri Relativi I Numeri Naturali I Numeri Reali
Ripasso di matematica Aritmetica e numeri
Aritmetica Geometria Informatica
Geometria Piana e Solida Informatica Media Ecdl
Elementi Fondamentali della Geometria Gli Angoli Il Triangolo Il Cerchio Linee sul Piano Quadrilateri e Poligoni Superficie dei Poligoni Cilindri e Prismi Coni e Piramidi Gli Esaedri La Sfera Geometria Solida Nozioni Generali Solidi di Rotazione
![]()
![]()
Definizione di numero razionale
Operazioni coi numeri razionali: somma
Frazioni decimali e numeri periodici
Potenza e radice quadrata di un numero razionale
Vantaggi e svantaggi dei numeri razionali relativi
Video:
Definizione di numero razionale
Potenza di un numero razionale
Radice quadrata di un numero razionale
![]()
![]()
MATEMATICA - I NUMERI RAZIONALI
I Numeri Razionali
DEFINIZIONE DI «NUMERO RAZIONALE»
Un treno è composto di 7 vetture, compresa la motrice;4 vetture sono di seconda classe, 2 altre di prima.
Come possiamo esprimere il fatto che il treno è suddiviso in queste parti, e come indicarlo?
Una carrozza su 7 è la motrice:
diciamo che essa costituisce 1/7 del treno.
Due carrozze su 7 sono di prima classe:
esse costituiscono i 2/7 del treno; infine 4 carrozze su 7 sono di seconda classe:
esse costituiscono i 4/7 del treno.
I numeri 1/7, 2/7, 4/7 si dicono numeri razionali, scritti in forma frazionaria.
«Frazione» vuol dire parte, indica un pezzo di un intero.
Così, ad esempio, l'ossigeno costituisce circa 1/5 dell'aria che respiriamo, mentre i 4/5 sono costituiti dall'azoto (in realtà, ci sono nell'aria anche altri gas e anidride carbonica, ma in quantità talmente irrilevanti che non ne abbiamo tenuto conto nella nostra suddivisione).
Abbiamo visto fin qui esempi di frazioni tratti dalla nostra vita quotidiana;
ora vediamo un esempio tratto dalla geometria.
Se noi dividiamo un segmento AB, una volta fissata un'unità di misura u, in 8 parti, ognuna di esse è 1/8 del segmento:
scriviamo 1/8 AB e leggiamo «un ottavo di AB».
Vogliamo ora trovare i 3/4 del segmento AB.
Cosa vuol dire ciò?
Dobbiamo fare due operazioni:
dividere il segmento AB in 4 parti, e prenderne poi 3.
Scritto coi numeri:
(8:4)x3 = 6.
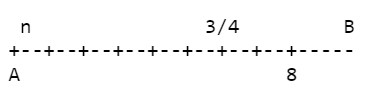
Si può notare già da ora come l'idea di frazione sia connessa all'idea di divisione.
Vedremo infatti che nei numeri razionali la divisione sarà sempre possibile.
Cos'è quindi un numero razionale?
Per numero razionale s'intende un numero che è rappresentabile come una frazione.
Esso può essere positivo o negativo.
Perciò si parla di numeri razionali relativi.
In una frazione il numero scritto sopra la sbarretta orizzontale si chiama numeratore, il numero scritto sotto si chiama denominatore.
Ad esempio, nella frazione:
3 --- 5il numero 3 è il numeratore e il numero 5 è il denominatore.
La frazione «tre quinti» può anche essere scritta (come qualsiasi altra frazione) 3/5.
Anche se tratteremo in seguito più diffusamente la divisione insieme con le altre operazioni, diciamo subito che un numero frazionario può leggersi come una divisione indicata, anche se non eseguita.
Così 4/5 può leggersi come 4:5, 3/7 come 3:7,-(5/3) come -5:3 oppure come 5:-3, ricordando le regole dei segni.
Capiamo subito perché ora possiamo sempre eseguire la divisione:
possiamo dire che ogni numero razionale in forma frazionaria è una divisione.
Traiamo perciò la seguente conclusione:
Ogni numero intero, positivo o negativo, può essere considerato come una frazione con denominatore 1.
E' quindi anche un numero razionale.
Infatti 5 può essere visto come 5/1 cioè 5:1 = 5, -10 come -10/1 cioè -10:1 = -10, e così via.
Sappiamo già che 0:5 = 0, poiché l'unico numero che moltiplicato per 5 da 0 è proprio lo 0.
La frazione 0/5 è quindi 0.
Ogni frazione il cui numeratore è 0 rappresenta il numero razionale 0.
Inoltre 3:0 = nessun numero, poiché qualsiasi numero moltiplicato per 0 dà 0:
siffatta divisione è impossibile.
Così pure 0:0 = qualsiasi numero, poiché ogni numero moltiplicato per 0 dà 0:
tale divisione è indeterminata.
Concludevamo dunque, a suo tempo, che a:0 oppure 0:0 non ha senso.
Anche per le frazioni diciamo:
Ogni frazione con denominatore 0 non ha significato:
in particolare non ha significato 0/0.
Definizione di numero razionale
PROPRIETA' DELLE FRAZIONI
Analizziamo la seguente situazione.Supponiamo che il percorso Roma-New York sia servito da due aerei;
il primo, che chiamiamo A, effettua 6 scali compreso quello di arrivo;
il secondo, B, ne compie uno sì e l'altro no.
Ora, una persona afferma di aver toccato, usando l'aereo B, i 2/3 degli scali;
un altra persona, viaggiando su A, ne ha toccati invece i 4/6.
A quale scalo si sono fermate?
Cerchiamo di tradurre in numeri il problema.
Consideriamo il percorso della persona che si è servita dell'aereo B:
ha toccato i 2/3 degli scali.
Sappiamo che ciò vuol dire:
divido 6 in 3 parti uguali e ne prendo 2;
in numeri:
(6:3)x2 = 4.
Consideriamo adesso il percorso dell'altra persona:
ha toccato i 4/6 dei 6 scali.
Questo vuol dire:
divido 6 in 6 parti e ne prendo 4;
in numeri: (6:6)x4 = 4.
Anche chi è salito sull'aereo A si trova dunque, attualmente, al quarto scalo.
Concludiamo che 4/6 e 2/3 rappresentano lo stesso numero razionale:
si tratta insomma di frazioni equivalenti.
Diciamo perciò:
Due frazioni sono equivalenti quando il numeratore e il denominatore di una di esse è ottenuto moltiplicando o dividendo il numeratore e il denominatore dell'altra frazione per uno stesso numero, positivo o negativo.
Infatti 8/12 = (4x2)/(6x2), 4/6 = (8:2)/(12:2).
Anche 2/3 è equivalente a 4/6, poiché 2/3 = (4:2)/(6:2).
Data una frazione ne esistono infinite altre equivalenti ad essa.
Partendo con 3/4 possiamo così ottenere, moltiplicando per un numero intero relativo per volta a partire da 1:
3/4, 6/8, 9/12, 12/16, 15/20,...
Inoltre 7 è equivalente a 7/1, 14/2, 21/3, ecc., da cui concludiamo:
Se il numeratore è divisibile per il denominatore, la frazione è equivalente a un numero intero, ottenuto eseguendo la divisione.
Queste proprietà delle frazioni ci permettono di semplificare una frazione.
La semplificazione è possibile a condizione di trovare un divisore comune del numeratore e del denominatore;
tale divisore deve essere il più grande per evitare di dover ripetere l'operazione.
Quando la semplificazione non può aver luogo, si dice che la frazione è irriducibile o che è ridotta ai minimi termini.
Una frazione è ridotta ai minimi termini quando numeratore e denominatore sono primi tra loro.
Si riduca ai minimi termini la frazione 80/25.
Divido numeratore e denominatore 80/25 = (80:5)/(25:5) = 16/5. 16 e 5 sono primi tra loro e la frazione è ridotta ai minimi termini.
Ma noi conosciamo già un metodo per trovare i divisori comuni di due numeri:
basta calcolare il M.C.D.
Facciamo un esempio:
ridurre ai minimi termini la frazione 810/330. Calcolo il M.C 810 e 330:

Quindi M.C.D (810,330) = 2x3x5 = 30
Allora 810/330 = (810:30)/(330:30) = 27/11, che è irriducibile ed equivalente alla data.
Un'altra proprietà importante delle frazioni è la riducibilità allo stesso denominatore.
E' in pratica il problema inverso al precedente e ci renderemo conto del perché.
Ad esempio vogliamo ridurre allo stesso denominatore le frazioni irriducibili 3/5, 4/7, 7/10.
E' necessario che tale denominatore sia multiplo di ciascuno dei denominatori delle frazioni date, cioè di 5, di 7, di 10.
Poiché i multipli di un numero sono infiniti prendiamo il minore di essi, cioè il m.c.m.
Nel nostro caso il m.c.m. è 70. Dividiamo ora il m.c.m. per ciascuno dei denominatori:
70:5=14, 70:7=10;
70:10=7, e moltiplichiamo i termini di ogni frazione per il quoto ottenuto, rispettivamente 3/5 = (3x14)/(5x14) = 42/70, 4/7 = (4x10)/(7x10) = 40/70, 7/10 = (7x7)/(10x7) = 49/70.
Otteniamo alla fine frazioni equivalenti alle date, aventi però lo stesso denominatore.
La regola si può enunciare così:
Ridurre delle frazioni al minimo comune denominatore vuol dire:
a) si riducono le frazioni ai minimi termini;
b) si trova il m.c.m. dei denominatori delle frazioni ridotte;
c) si divide il m.c.m. per ciascuno dei denominatori;
d) si moltiplica il quoto così ottenuto per entrambi i termini di ciascuna frazione.
Si è soliti dividere le frazioni nei seguenti modi.
Una frazione si dice propria se il numeratore è minore del denominatore;
si dice impropria se il numeratore è maggiore del denominatore;
è apparente se il numeratore è multiplo del denominatore, se cioè la frazione è equivalente a un numero intero.
ORDINAMENTO
Sappiamo che stabilire un ordinamento tra numeri vuol dire essere in grado di decidere, dati numeri qualunque, quale di essi è maggiore o minore.Analizziamo, ad esempio, il comportamento di due ascensori.
In un tempo fissato, l'ascensore A compie 1/2 del percorso;
l'ascensore B nello stesso tempo compie 1/4 del percorso.
Qual è l'ascensore più veloce?
Si tratta di confrontare i numeri 1/2 e 1/4 e vedere quale dei due è maggiore.
Dobbiamo allora trovare frazioni equivalenti alle date che abbiano lo stesso denominatore.
Calcoliamo il m.c.m. che è 4.
Abbiamo =1/2 = (1x2)/(2x2) = 2/4; 1/4 = (1x1)/(4x1) = 1/4;
si vede subito che 2/4 > 1/4, poiché di 4 parti nel primo caso ne prendo due, nel secondo una sola, e 2 > 1.
Concludiamo con la regola:
Per stabilire se una frazione è maggiore di un'altra dobbiamo distinguere due casi:
a) se le frazioni hanno ugual denominatore, è maggiore la frazione con numeratore maggiore;
b) se le frazioni hanno denominatori diversi esse vanno ridotte allo stesso denominatore ed è maggiore quella frazione con numeratore maggiore.
Anche i numeri razionali sono totalmente ordinati;
considerando anche le frazioni negative, diciamo che ogni numero positivo compreso lo zero è maggiore di ogni numero negativo;
ogni frazione propria è compresa tra 0 e 1 se positiva.
Scritto in lettere, questo vuol dire:
per ogni numero intero positivo a, b, con a b, si ha che 0 a/b 1.
L'ultima osservazione ci fa capire un'importante diversità dell'ordinamento dei numeri razionali rispetto a quello dei numeri interi: esso gode di una nuova proprietà.
Mentre tra 0 e 1 non c'è nessun numero intero, abbiamo visto che invece ci sono infiniti razionali.
Per convincercene possiamo porre a = 1 e b > 1.
Facendo assumere a b tutti i valori positivi maggiori di 1, abbiamo:
0 1/2, 1/3, 1/4,..., 1/1000,..., 1
Il fatto importante è che questo fenomeno non si verifica solo tra O e 1.
Possiamo dire in generale:
Fra due numeri razionali ve ne sono infiniti altri.
Questa proprietà dell'ordinamento si chiama densità.
Al contrario, l'ordinamento dei numeri interi si dice discreto.
Diamo un esempio in cui si verifica facilmente la proprietà enunciata.
Consideriamo due frazioni qualsiasi, 1/10 e 1/3;
riduciamole allo stesso denominatore, passando così a due frazioni equivalenti alle date, cioè 3/30 e 10/30.
Abbiamo 3/30 10/30, ma fra queste due sono comprese anche le frazioni 4/30, 5/30, ..., 9/30;
ripetendo il procedimento per altre due di queste, otteniamo ancora frazioni comprese tra loro e quindi tra le nostre due frazioni originarie 1/10 e 1/3, e questo procedimento non ha mai fine.
Ritorniamo alla rappresentazione dei numeri interi sulla retta.
I numeri interi non individuano tutti i punti della retta:
per passare da 0 a 1, ad esempio, si deve fare un salto.
Ora, i numeri razionali servono proprio a riempire gli spazi tra numeri interi.
Poniamoci una domanda:
i numeri razionali riempiono tutti gli spazi?
I numeri razionali individuano tutti i punti della retta?
A questa domanda, che per ora lasciamo in sospeso, risponderemo brevemente più tardi.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
OPERAZIONI COI NUMERI RAZIONALI: SOMMA
Quando estendiamo la somma ai numeri razionali, l'unica difficoltà in cui ci imbattiamo è che ora abbiamo a che fare con frazioni.Per il resto valgono esattamente le stesse proprietà.
Osserviamo la figura 53.
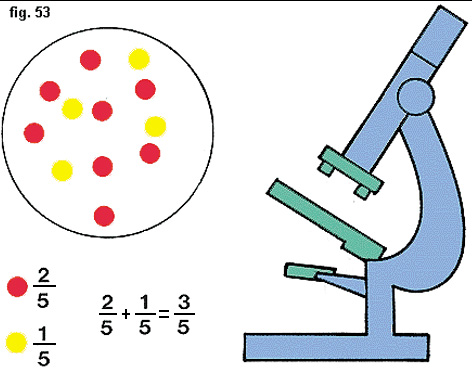
Sono indicate le componenti del sangue e il rapporto tra le loro singole quantità rispetto alla totalità del liquido.
Se vogliamo sapere quanta parte occupano i globuli rossi e i globuli bianchi, sommario 2/5 + 1/5 = 3/5.
Ugualmente, se dividiamo un segmento in 5 parti, prendendone prima 2 (cioè i 2/5) poi 1 (cioè 1/5) e vogliamo sapere quante parti prendiamo in tutto, eseguiamo ancora 2/5 + 1/5 = 3/5.
Possiamo concludere che:
Se le frazioni hanno tutte lo stesso denominatore, la loro somma è una frazione che ha lo stesso denominatore e per numeratore la somma algebrica dei numeratori.
Abbiamo parlato di somma algebrica, poiché può darsi che le frazioni siano negative.
Ad esempio 5/6 - 1/6 + 2/6 = (5-1)/6 + 2/6 = 6/6 = 1.
Se invece le frazioni da sommare hanno denominatore diverso, bisogna prima ridurle al minimo comune denominatore:
si è così ricondotti al caso precedente.
Se la frazione è riducibile, va semplificata;
altrimenti si procede subito alla riduzione al minimo comune denominatore.
Ad esempio:
5/9 + 7/4.
Nessuna delle due è riducibile;
calcoliamo allora il m.c.m. per ridurre le frazioni a frazioni equivalenti con lo stesso denominatore:
5/9 = 5x4/9x4 = 20/36; 7/4 = 7x9/4x9 = 63/36;
eseguendo la somma otteniamo 83/36.
Più rapidamente si può procedere così:
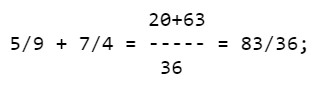
il numeratore è uguale alla somma dei termini ottenuti dividendo per 36 ciascun denominatore e moltiplicando il quoto per ogni numeratore.
Cioè 20 = (36:9)x5, 63 = (36:4)x7.
L'addizione di frazioni gode delle proprietà commutativa e associativa, proprio come i numeri interi.
Nella definizione di somma di frazioni avevamo implicitamente considerato anche la differenza di frazioni, poiché abbiamo parlato di somma algebrica.
La regola per la sottrazione è infatti identica.
Abbiamo così che i numeri razionali relativi sono chiusi rispetto alla somma e alla differenza.
Osserviamo la figura 54.
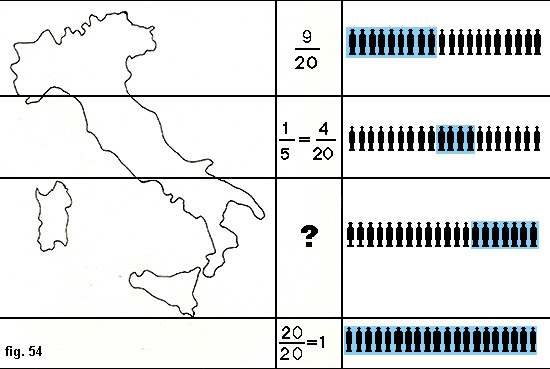
Se conosciamo la parte della popolazione totale residente in Italia settentrionale e centrale e vogliamo trovare la parte della popolazione residente in Italia meridionale e insulare procediamo così:
prima sommiamo le parti note:ma sommiamo le parti note:
9/20 + 1/5 = 13/20.
Sappiamo ora che insieme la popolazione residente al Nord e al Centro costituisce i 13/20 della popolazione totale, che indichiamo con 1.
Volendo conoscere la parte di popolazione residente nel Sud calcoliamo 1-13/20 = 20/20-13/20 = 7/20.
Infatti qui 1 sta per 20/20.
Nel Sud e nelle Isole risiedono dunque i 7/20 della popolazione italiana.
La frazione 7/20 si chiama frazione complementare di 13/20.
Diciamo quindi:
La differenza tra l'unità e una frazione propria si dice frazione complementare di quest'ultima.
Così la frazione complementare di 1/3 è 1-1/3 = 2/3.
Per riconoscere se due frazioni sono complementari basta verificare che la loro somma sia l'unità.
Sono complementari 5/7 e 2/7?
Eseguiamo la somma 5/7 + 2/7 = 1:
le frazioni sono complementari; 3/5 è complementare di 1/5?
Eseguiamo:
3/5 + 1/5 = 4/5:
non è complementare.
Se a qualsiasi frazione aggiungiamo 0 otteniamo la frazione di partenza.
Anche qui 0 è elemento neutro rispetto alla somma.
Opposta di una frazione è una frazione uguale in valore assoluto ma di segno diverso.
Operazione coi numeri razionali: somma e sottrazione
PRODOTTO
Anche il prodotto di due frazioni non presenta difficoltà.Esso gode delle stesse proprietà commutativa e associativa, oltre che della proprietà distributiva rispetto alla somma.
Diciamo che:
Il prodotto di due frazioni è una frazione che ha per numeratore il prodotto dei numeratori e per denominatore il prodotto dei denominatori.
Ad esempio 5/3x6/2 = 30/6 = 5; 3/5x1/6 = 3/30 = 1/10.
Quando si moltiplicano due o più frazioni può capitare (vedi gli esempi precedenti) che il numeratore di una e il denominatore dell'altra abbiano un divisore comune.
Nell'esempio fatto sopra, nel primo prodotto 3 e 6 hanno un divisore comune, che è 3.
In questi casi, prima di eseguire il prodotto si divide il numeratore e il denominatore in questione per il loro divisore comune.
Analogamente a quanto succede per gli interi:
quando uno dei fattori è 0, il prodotto è 0.
Inoltre:
il prodotto di una frazione per l'unità è uguale alla frazione stessa.
Infatti ciò equivale a moltiplicare numeratore e denominatore per 1.
Si dice che 1 è elemento neutro rispetto al prodotto.
Consideriamo la frazione 3/7;
se scambiamo di posto numeratore e denominatore otteniamo la nuova frazione 7/3, che si dice inversa della precedente.
Diciamo che:
una frazione è inversa di un'altra se il risultato della loro moltiplicazione è l'unità, cioè l'elemento neutro rispetto al prodotto. Così 7/3x3/7 = 1.
Dato un qualsiasi numero razionale esiste sempre ed è un numero razionale l'inverso del numero dato.
Poiché ogni numero intero è un numero razionale, esisterà anche l'inverso di 3 che è 1/3, di 5, che è 1/5 e così via.
Notiamo che questa è una novità rispetto a quanto abbiamo osservato finora a proposito delle operazioni.
Se consideriamo «passare all'inverso di un numero dato» come un'operazione, possiamo scrivere a i→ b dove b è tale che bxa = 1.
La lettera i indica l'operazione di invertire un numero.
Ad esempio:
3 i→ 1/3 poiché 3x1/3 = 1; 7/5 i→ 5/7, poiché 7/5x5/7 = 1.
DIVISIONE
Abbiamo già fatto notare come un numero frazionario possa essere considerato come l'indicazione di una divisione.Vediamo ora la divisione di una frazione per un'altra.
In generale si ha che:
Per dividere una frazione per un'altra basta moltiplicare la prima per l'inversa della seconda.
Così:
7/10:3/5 = 7/10x5/3 = 7/6.
Poiché:
1) l'inversa di una frazione è ancora una frazione;
2) il prodotto di due frazioni è una frazione, abbiamo che:
i numeri razionali sono chiusi rispetto alla divisione, nel senso che, dati due numeri razionali qualsiasi, esiste ed è un numero razionale il loro quoto.
E' così raggiunto lo scopo che ci aveva spinti a passare a un nuovo tipo di numeri.
Una frazione si dice a termini frazionari, quando o il numeratore o il denominatore o entrambi sono delle frazioni.

la frazione precedente diventa 2/3:5/7 = 2/3x7/5 = 14/15.
Questo fatto ci permette di chiarire meglio il passaggio da una frazione alla sua inversa.
Si ha che 3/5 i→ 5/3, ma 5/3 può essere considerato il quoto della divisione 1:3/5 = 1x5/3 = 5 /3.
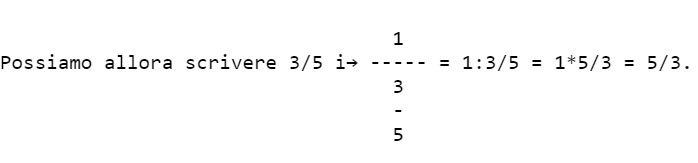
a i→ 1/a e si verifica che ax1:a = 1.
Operazione coi numeri razionali: divisione
FRAZIONI DECIMALI E NUMERI PERIODICI
Sappiamo che ogni numero intero può essere rappresentato come frazione il cui denominatore è 1 e il cui numeratore è uguale a quel numero.Poiché una frazione indica una divisione, possiamo notare che, eseguendo la divisione, ogni frazione propria o impropria può scriversi come numero decimale. Infatti 2/5 = 2:5 = 0,4; 7/8 = 7:8 = 0,875.
A sua volta ogni numero decimale può trasformarsi in una frazione, secondo la seguente regola:
Un numero decimale si trasforma in una frazione il cui numeratore è il numero senza la virgola, e il cui denominatore è l'unità seguita da tanti zeri quante sono le cifre decimali del numero.
Ad esempio 2,85 = 285/100 = 57/20.
La frazione 285/100 si chiama frazione decimale.
In genere una frazione decimale è una frazione il cui denominatore è 10 o una potenza di 10.
Inversamente:
Ogni frazione decimale si trasforma in un numero decimale, scrivendo il numeratore e mettendo la virgola dopo tante cifre a partire da destra quanti sono gli zeri del denominatore.
Ad esempio 41/100 = 0,41; 353/10 = 35,3.
Quando eseguiamo il passaggio da una frazione qualunque al numero decimale, dividendo il numeratore per il denominatore, possiamo cadere in due casi.
O la divisione ha una fine, ed è questo il caso che abbiamo visto finora;
allora il numero decimale si dice limitato, essendo il numero delle cifre finito.
Oppure la divisione non ha mai fine;
ad esempio 5/7 = 5:7 = 0,714285714285.... 1/3 = 1:3 = 0,3333..., 1/11 = 0,09090...
In questo secondo caso, il quoziente è un numero decimale le cui cifre decimali sono illimitate e continuano a ripetersi nello stesso ordine:
nel primo esempio si ripetono sempre le cifre 714285, nel secondo il 3, nel terzo il 90.
Tale numero decimale si dice illimitato, mentre il gruppo di cifre che si ripete si chiama periodo.
I numeri che si comportano in tal modo sono detti numeri decimali periodici.
Per evitare di scrivere tutte le cifre del periodo (sarebbe impossibile!) si suole indicarle con una sbarretta sopra di esse;
possiamo così scrivere nell'ordine i numeri precedenti segnando la parte periodica:

I primi sono detti numeri periodici semplici;
i secondi, numeri periodici misti.
Nei numeri periodici misti, il gruppo di cifre che segue la virgola e che precede il periodo viene detto antiperiodo («davanti al periodo»).
Poniamoci ora i seguenti problemi:
1° Data una frazione ordinaria, trasformarla in un numero decimale illimitato.
2°. Dato un numero decimale illimitato, trasformarlo in una frazione.
Prima di affrontarli, diamo due definizioni:
1) Una frazione si dice ordinaria quando non è decimale.
2) Si chiama frazione generatrice di un numero decimale la frazione da cui si parte per ottenere il numero in questione.
(Esempio: 7/5 genera il numero decimale 1,4, poiché 7:5 = 1,4).
Grazie al nuovo termine da noi introdotto, il secondo problema può essere enunciato così:
dato un numero decimale illimitato, trovare la sua frazione generatrice.
Cominciamo dal primo problema.
I passi da fare sono:
ridurre la frazione ai minimi termini;
assicurarsi se il denominatore contiene i fattori 2 e 3;
se li contiene, eseguire la divisione del numeratore per il denominatore.
Otteniamo così un numero decimale limitato;
ma questo non va bene poiché noi volevamo trasformare la frazione in un numero decimale illimitato.
Abbiamo allora:
Una frazione si trasforma in un numero decimale limitato se il denominatore ha come fattori primi o solo 2 o solo 5 oppure solo 2 e 5.
Prendiamo come esempio 24/40.
Riduco ai minimi termini:
3/5; il denominatore è 5;
eseguo la divisione 3:5 = 0,6, che è un numero decimale limitato.
Siccome il nostro scopo è di trovare il numero decimale illimitato in cui la frazione si trasforma, quando mi chiedo:
il denominatore contiene solo i fattori 2 o 5 o entrambi, e rispondo di sì, mi blocco, poiché so già che otterrò un numero decimale limitato.
Concludiamo allora risolvendo il primo problema così:
Una frazione si trasforma in un numero decimale illimitato se, una volta ridotta ai minimi termini il denominatore non contiene i fattori 2 e 5.
Prendiamo come esempio 42/98.
Semplifico ottenendo 21/49; mi chiedo:
il denominatore contiene 2 o 5? Verifico che no; allora eseguo la divisione,
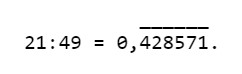
Se il denominatore della frazione ridotta ai minimi termini contiene, oltre ai fattori 2 o 5, altri fattori, allora ottengo un numero periodico misto.
Così ad esempio consideriamo la frazione 16/30.
Riducendo otteniamo 8/15;
troviamo i fattori primi del denominatore, scrivendo 8/3x5;
contiene solo 5? No.
Eseguiamo allora la divisione:
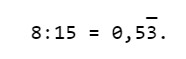
Il denominatore contiene solo 5 e 2? No.
Eseguo la divisione:
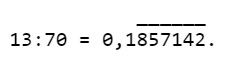
Qui di seguito è schematizzato il processo per risolvere il primo problema in entrambi i casi considerati.

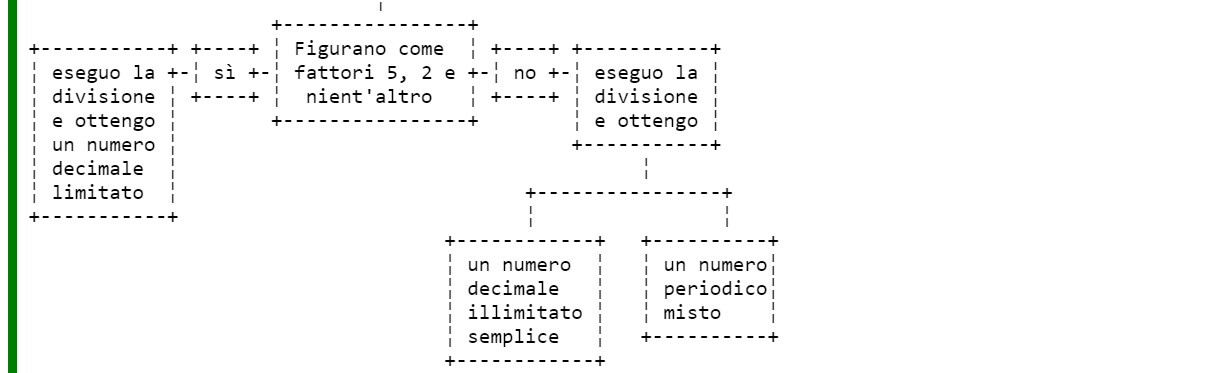
Passiamo ora al secondo problema:
dato un numero decimale illimitato, trovare la sua frazione generatrice.
Conosciamo già la soluzione quando il numero decimale è limitato.
Se invece il numero è decimale illimitato, distinguiamo due casi.
Primo caso:
il numero è periodico semplice.
Ecco tutti i passaggi richiesti: si contano le cifre del periodo:
si scrive una frazione il cui denominatore è formato da tanti 9 quante sono le cifre del , periodo;
il numeratore è la differenza tra l'intero numero considerato senza la virgola e il segno sulle cifre periodiche, e la parte intera;
si riduce ai minimi termini la frazione così ottenuta.
Esempio:
trovare la frazione generatrice di 0,31.
Le cifre del periodo sono due, quindi si ha:

Secondo caso:
il numero è periodico misto.
I passi da fare sono i seguenti.
Si contano le cifre del periodo e dell'antiperiodo;
si scrive una frazione il cui denominatore è un numero formato da tanti 9 quante sono le cifre del periodo e seguito da tanti 0 quante sono le cifre dell'antiperiodo;
il numeratore è la differenza tra l'intero numero scritto senza virgola e senza il segno sulle cifre periodiche, e il numero formato dalla parte intera seguita dall'antiperiodo;
si riduce la frazione così ottenuta ai minimi termini.
Alcuni esempi:
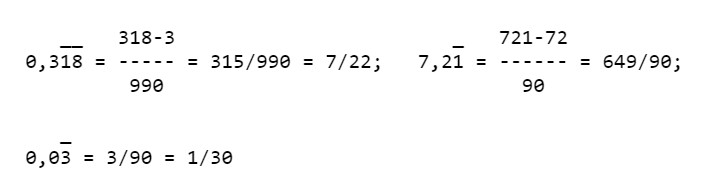
POTENZA E RADICE QUADRATA DI UN NUMERO RAZIONALE
Estendiamo anche ai numeri razionali queste operazioni già definite per i numeri interi.Ricordando che elevare a potenza n un numero vuol dire moltiplicarlo per se stesso n volte, abbiamo ad esempio: (2/3)2 = 2/3x2/3 = 4/9.
La potenza di una frazione è uguale alla frazione ottenuta elevando a quella potenza numeratore e denominatore.
Valgono le stesse proprietà già viste in precedenza.
Nel caso dei numeri interi ci eravamo però soffermati a considerare solo esponenti uguali o maggiori di 0.
Un grande vantaggio dei numeri razionali e invece che essi sono chiusi rispetto all'operazione di potenza per un qualunque esponente anche negativo.
Consideriamo questo esempio: 3-2 .
Ricordando le proprietà delle potenze abbiamo 3-2 = 33-5 = 33 :35 , e poiché una divisione è una frazione, possiamo scrivere 3-2 = 33 / 35 .
Semplificando abbiamo 1/32 .
In conclusione 3-2 = 1/32 .
Diciamo allora:
Una potenza con esponente negativo è uguale all'inverso della potenza con lo stesso esponente positivo.
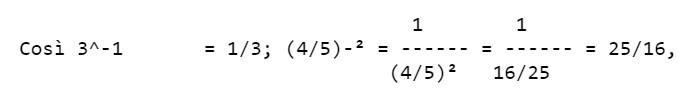
E' importante prendere in considerazione, per l'uso frequente che se ne fa nelle misurazioni di oggetti piccolissimi, le potenze a base 10 con esponente negativo.
Il seguente schema ne è un'illustrazione.

Si ha che la radice quadrata di una frazione è uguale alla frazione che ha come numeratore la radice quadrata del numeratore e come denominatore la radice quadrata del denominatore.
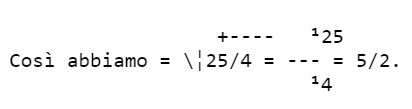
Osserviamo per prima cosa che le radici trovate finora sono radici quadrate di numeri detti quadrati perfetti.
Un numero è un quadrato perfetto se per esso esiste la radice quadrata esatta.
Così 0, 1, 4, 9, 16, 25, 36,... (cioè i quadrati dei numeri naturali 0, 1, 2, 3, 4, 5, 6,... sono quadrati perfetti.
Se un numero non è tale, la radice quadrata si calcola per approssimazione, potendosi così ottenere un numero con cifre decimali illimitate, ma non periodico.
Ci troviamo così di fronte a un nuovo tipo di numeri, che non sono razionali perché non sono periodici, e quindi non se ne può trovare la frazione generatrice.
Diciamo allora:
La radice quadrata di un numero che non è un quadrato perfetto è un numero irrazionale.
Facciamo un solo esempio, però assai importante per la sua origine storica.
Fu il matematico greco Pitagora a scoprire i numeri irrazionali, anche se non li chiamò in questo modo.
Consideriamo un triangolo rettangolo i cui cateti misurano entrambi 1 cm, e calcoliamo la misura dell'ipotenusa.
Applicando il teorema di Pitagora (v. Superfici dei poligoni) e chiamando con la lettera a l'ipotenusa, abbiamo:
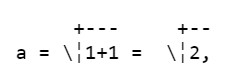
Possiamo quindi affermare che:
i numeri razionali non sono chiusi rispetto all'estrazione dea radice quadrata.
Detto per inciso, ci siamo sempre limitati al caso in cui il radicando è maggiore o uguale a 0;
ma cosa succede se si toglie questa condizione e come radicando prendiamo qualsiasi numero razionale anche negativo?
Lasciamo questo interrogativo aperto a causa della complessità dei problemi che sorgerebbero se solo tentassimo una risposta.
Chiamiamo i numeri razionali e irrazionali numeri reali.
Non parleremo però delle proprietà dei numeri reali, e procederemo piuttosto con un'ultima osservazione sui numeri razionali.
Potenza di un numero razionale
Radice quadrata di un numero razionale
VANTAGGI E SVANTAGGI DEI NUMERI RAZIONALI RELATIVI
A questo punto, come abbiamo fatto per gli interi tentiamo un «bilancio» per valutare aspetti positivi e negativi, connessi all'introduzione dei numeri razionali relativi.Non abbiamo perduto nessuna delle proprietà stabilite per i numeri interi;
anzi, i due problemi aperti sono stati risolti, poiché la divisione ora è sempre eseguibile, come pure è sempre eseguibile l'elevamento a potenza, per qualsiasi numero intero come esponente.
Inoltre siamo nelle condizioni di capire una parte di realtà ancora più ampia, quella che riguarda l'uso delle frazioni.
L'unico grande problema ancora aperto riguarda la radice quadrata, perché i numeri razionali non sono chiusi rispetto a quest'operazione.
Ricordando la rappresentazione sulla retta di tali numeri possiamo ora capire perché, mentre a un numero razionale corrisponde un punto della retta, non a ogni punto della retta corrisponde un numero razionale.
Ci sono cioè dei «buchi», e questi sono proprio i numeri irrazionali come √2.
E' possibile infatti rappresentare √2 sulla retta in questo modo:
consideriamo il triangolo rettangolo di base 1 e altezza 1;
puntando il compasso in 0 con apertura uguale all'ipotenusa, la cui misura è √2, riportiamo l'ipotenusa sulla retta:
il suo estremo individuerà un punto compreso tra 1 e 2, che è il punto designato da √2.
Poiché i numeri reali comprendono sia i numeri razionali che gli irrazionali, solo con i numeri reali possiamo dire:
a ogni punto della retta corrisponde un numero (reale).
Coi soli numeri razionali abbiamo già comunque un ambiente in cui è possibile eseguire tutte e quattro le operazioni aritmetiche fondamentali;
in altre parole:
I numeri razionali relativi sono chiusi rispetto alla somma, alla differenza, al prodotto e alla divisione.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()
Visite da:
Jesi Marche Geografia Marche Comune di Jesi Provincia di Ancona Regione Marche
![]()
