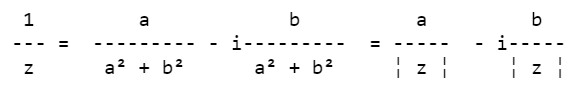|
Differenza di due numeri complessi Prodotto di due numeri complessi Rappresentazione di Gauss dei numeri complessi Ripasso di matematica Aritmetica e numeri I Numeri razionali Immaginari Relativi Naturali Reali Aritmetica Geometria Informatica Geometria Piana e Solida Informatica Media
MATEMATICA - I NUMERI COMPLESSIAbbiamo visto che da numeri reali possiamo ottenere numeri immaginari prendendo le radici di ordine pari di numeri negativi, e da numeri immaginari possiamo ottenere numeri reali con le operazioni di prodotto e divisione; ma ciò non è sufficiente. Cerchiamo, per esempio di calcolare il valore di √i, di trovare cioè quel numero che moltiplicato per sé stesso dia i; esso non sarà un numero reale in quanto un numero reale moltiplicato per un numero reale dà un numero reale; non sarà neppure un numero immaginario poiché un numero immaginario moltiplicato per un numero immaginario dà un numero reale. Allora il valore di √i non esiste? Il valore di √i esiste ma dobbiamo cercarlo non nei numeri reali né nei numeri immaginari bensì nell'unione dei due tipi di numeri che prendono il nome di numeri complessi. Un numero complesso z si indica nel seguente modo: z = a + ib dove il simbolo + non ha un vero significato di somma ma serve per separare la parte reale, a, dalla parte immaginaria, b, del numero z. In molti testi la notazione per indicare il numero complesso z è la seguente: z = (a,b) dove al primo posto della coppia di numeri c'è la parte reale a, mentre al secondo posto della coppia c'è la parte immaginaria b. Noi utilizzeremo il primo modo di indicare un numero complesso. E' bene far notare che nella notazione z = a + ib l'unità immaginaria i serve per identificare la parte immaginaria del numero complesso, serve cioè da identificatore. Un numero complesso è quindi formato da una parte reale e una parte immaginaria e se la parte immaginaria è nulla allora il numero complesso è reale, se invece è nulla la parte reale il numero complesso è immaginario puro. Si vede quindi che i numeri reali e i numeri immaginari sono casi particolari dei numeri complessi. Nell'insieme dei numeri complessi definiscono le seguenti operazioni: dati due numeri complessi z = a + ib e w = c + id.
SOMMA DI DUE NUMERI COMPLESSI z + w = (a + ib) + (c + id) = (a+c) + i(b+d) cioè la somma di due numeri complessi si ottiene sommando la parte reale del primo numero complesso con la parte reale del secondo numero e sommando la parte immaginaria del primo numero con la parte immaginaria del secondo numero complesso.
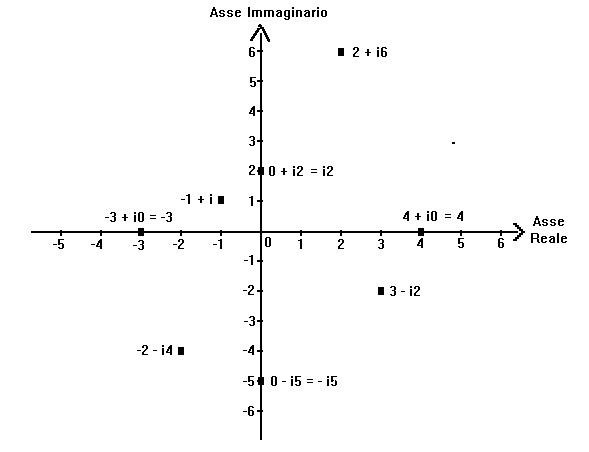
DIFFERENZA DI DUE NUMERI COMPLESSI z - w = (a + ib) - (c + id) = (a-c) + i(b-d) cioè la differenza fra due numeri complessi si ottiene sottraendo la parte reale del secondo numero complesso dalla parte reale del primo e sottraendo la parte immaginaria del secondo numero dalla parte immaginaria del primo. PRODOTTO DI DUE NUMERI COMPLESSI z x w = (a + ib) x (c + id) = (ac -bd) + i(ad + bc) cioè il prodotto fra due numeri complessi si ottiene: per la parte reale, il prodotto delle parti reali dei due numeri complessi meno il prodotto delle parti immaginarie dei due numeri complessi; la parte immaginaria si ottiene moltiplicando la parte reale del primo numero complesso per la parte immaginaria del secondo numero complesso più il prodotto della parte immaginaria del primo numero complesso per la parte reale del secondo numero complesso. Esiste un'utile rappresentazione grafica dei numeri complessi nota come "rappresentazione di Gauss". Se rappresentiamo la parte reale dei numeri complessi lungo una retta orizzontale e la parte immaginaria lungo una retta verticale perpendicolare alla retta orizzontale, un numero complesso z sarà rappresentato da un punto del piano formato dalle due rette, mentre ad ogni punto del piano corrisponderà un numero complesso (vedi figura). Rappresentazione di Gauss dei numeri complessi
Si definisce il complesso coniugato di un numero complesso z = a + ib il numero, sempre complesso, ottenuto cambiando di segno alla parte immaginaria di z e si indica con: - z = a - ibIl prodotto di un numero complesso z = a + ib per il suo complesso coniugato è sempre un numero reale e vale: _ Il reciproco di un numero complesso z = a + ib è dato da:
Noto il reciproco di un numero complesso possiamo definire la divisione fra due numeri complessi z = a + ib e w = c + id :
L'elevamento a potenza reale di un numero complesso viene definito nel modo usuale, cioè: zn = (a + ib)3 = (a + ib) x (a + ib) x ........x (a + ib) n volte. Facendo i prodotti a due a due con le regole del prodotto già viste è possibile calcolare qualsiasi potenza di z. Con l'introduzione dei numeri complessi nella matematica è risultato possibile risolvere equazioni non risolubili nell'insieme dei numeri reali e rendere più semplice la trattazione di problemi legati alla trasmissione delle onde in fisica oppure alle correnti elettriche dipendenti dal tempo in elettronica. E la nostra √i che fine ha fatto? Quanto vale allora? A titolo di esempio mostriamo le procedure per il calcolo lasciando come esercizio il calcolo di √-i. Il valore di √i sarà un numero complesso z tale che, per la definizione di radice quadrata si ha: z2 = i Sia z = a + ib allora z2 = (a + ib)2 = (a + ib) x (a + ib) = a2 - b2 + i2ab = i Poiché z2 = i ha parte reale nulla e parte immaginaria uguale a 1 si ottiene: a2 + b2 = 0 (parte reale di z2 ) 2ab = 1 (parte immaginaria di z2 ) Dalla prima equazione si ottiene: a2 = b2 e quindi a = b sostituendo questo valore nell'equazione 2ab = 1 otteniamo: 2a2 = 1 e quindi a = ±√1/2 e b = ±√1/2 Poiché il prodotto 2ab = 1 è chiaramente positivo, a e b devono avere i segni concordi, cioè entrambi positivi o entrambi negativi. Il numero complesso z cercato è: z = √1/2 + i√1/2 e anche z = -√1/2 - i√1/2 In conclusione abbiamo che: √i = ±(√1/2 + i√1/2).
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte Storia Antica e Medievale Storia Moderna e Contemporanea Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9 Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
|