Lettura e stampa per righe di una matrice
Lettura e stampa per colonne di una matrice
Somma di due matrici di dimensioni
Moltiplicazione di due matrici
Aritmetica Geometria Informatica
I Numeri complessi I Numeri Immaginari I numeri Relativi I Numeri Naturali I Numeri Reali I Numeri Razionali
Calcolo letterale e Equazioni di primo grado Equazioni di secondo grado Insiemi numerici
La proporzionalità Sistemi di numerazione
Ripasso di matematica Aritmetica e numeri
Geometria Piana e Solida Informatica Media
Angoli Cerchio Triangolo Linee sul Piano Quadrilateri Poligoni Superficie dei Poligoni
Cilindri e Prismi Coni e Piramidi Esaedri Sfera Geometria Solida nozioni generali Solidi di rotazione
Rai Scuola I pitagorici e la scoperta dei numeri irrazionali
![]()
![]()
INFORMATICA - PROGRAMMAZIONE LE MATRICI
LE MATRICI
Una matrice è un insieme di valori tutti dello stesso tipo, cioè omogenei tra loro; si può pensare come ad una serie di caselle disposte in forma di tabella, su righe e colonne per una matrice a due dimensioni, o disposte su più piani per una a tre dimensioni; esistono anche matrici a più dimensioni, ma rappresentarle visivamente è piuttosto difficile (qual è la quarta dimensione?). Ogni casella viene chiamata elemento della matrice. Ogni elemento si distingue dagli altri in base alla sua posizione; naturalmente si deve precisare la posizione dell'elemento rispetto a ciascuna dimensione. I numeri corrispondenti alla posizione vengono detti indici dell'elemento e permettono di lavorare direttamente sull'elemento desiderato. In una matrice a due dimensioni, pensabile come formata da righe e colonne, ad ogni valore sono associati due indici, uno dei quali indica la posizione sulla colonna (cioè la riga cui il valore appartiene), l'altro la posizione sulla riga (cioè la colonna a cui il valore appartiene). In una matrice a tre dimensioni ad ogni elemento sono associati 3 indici, e in generale ad una matrice ad N dimensioni ad ogni elemento sono associati N indici. Il vettore è un caso particolare di matrice: una matrice ad una dimensione. Nel seguito del capitolo si farà riferimento soltanto a matrici a due dimensioni, anche quando il termine sarà usato genericamente; ogni esempio può però essere facilmente esteso a matrici a più dimensioni. Non esistono operazioni che agiscono sull'intera matrice; si lavora sempre su un elemento alla volta; per indicare su quale elemento agire si devono usare gli indici, che possono essere valori numerici costanti oppure variabili. Il numero contenuto nell'indice deve sempre fare riferimento ad un elemento valido altrimenti si verifica un errore di esecuzione.![]()
![]()
IL CARICAMENTO DELLA MATRICE
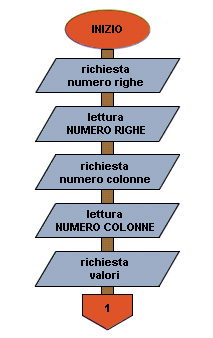
La lettura e la stampa di una matrice possono essere eseguite elemento per elemento, in modo sequenziale. Per scandire in modo sequenziale tutti gli elementi di una matrice bisogna procedere all'esame di un elemento alla volta, in un ciclo che percorra tutti gli elementi della matrice. Ciò può essere realizzato facilmente con due cicli FOR, uno interno all'altro, che fanno variare gli indici di riga e colonna. (Gli elementi della matrice vengono individuati sempre da due indici; per esaminare tutti gli elementi della matrice occorrono dunque due cicli nidificati). La scansione sequenziale degli elementi può essere eseguita per righe o per colonne.ESEMPIO 34
Lettura e stampa per righe di una matrice. Fissato l'indice di riga, viene letta la prima riga, facendo variare l'indice di colonna; poi si incrementa l'indice di riga e si legge la riga successiva, facendo nuovamente variare l'indice di colonna e così via, finché si esauriscono le righe. In modo analogo viene eseguita la scrittura per righe. Se si desidera che la stampa assuma l'aspetto tabellare proprio delle matrici, bisogna effettuare un posizionamento a capo dopo la stampa di ciascuna riga. Descrizione delle variabili:
Flow chart Esempio 34 (prima parte)
Flow chart Esempio 34 (seconda parte)
Pseudocodifica (vedi Figure)
1 inizio
2 emissione richiesta numero righe
3 lettura NUMERORIGHE
4 emissione richiesta numero colonne
5 lettura NUMEROCOLONNE
6 emissione richiesta valori
7 per INDICERIGA da 1 a NUMERORIGHE con passo 1
8 per INDICECOLONNA da 1 a NUMEROCOLONNE con passo 1
9 lettura MATRICE(INDICERIGA, INDICECOLONNA)
10 fine per
11 fine per
12 per INDICERIGA da
1 a NUMERORIGHE con passo 1
13 per INDICECOLONNA a NUMEROCOLONNE con passo 1
14 emissione MATRICE (INDICERIGA, INDICECOLONNA)
15 fine per
16 ritorno a capo riga
17 fine per
18 fine
2-3 Richiesta del numero di righe della matrice utilizzate.
4-5 Richiesta del numero di colonne della matrice utilizzate.
da 7 a 11 Inserimento dei valori nella matrice;
vengono usati due cicli FOR nidificati.
7 Il ciclo FOR più esterno viene ripetuto per un numero di volte pari a NUMERORIGHE cioè al numero di righe utilizzate;
ad ogni ciclo viene incrementata la variabile INDICERIGA.
8 Il ciclo FOR più interno viene ripetuto per un numero di volte pari a NUMEROCOLONNE, cioè al numero di colonne utilizzate, per ogni valore di INDICERIGA;
ad ogni ciclo viene incrementata la variabile INDICECOLONNA.
9 Lettura di un elemento della matrice;
l'elemento viene individuato dagli indici, cioè dai valori di INDICERIGA, che specifica la riga su cui si trova l'elemento, e INDICECOLONNA, che specifica la colonna su cui si trova l'elemento.
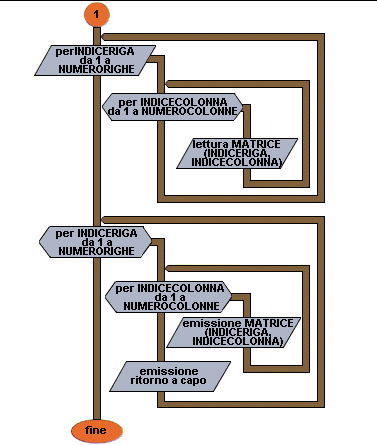
da 12 a 17 Stampa della matrice; vengono usati due cicli FOR nidificati.
Anche in questo caso nel ciclo FOR più esterno varia l'indice di riga e nel ciclo più interno l'indice di colonna.
14 Stampa di un elemento della matrice;
l'elemento viene individuato dagli indici, cioè dai valori di INDICERIGA, che specifica la riga su cui si trova l'elemento, e INDICECOLONNA, che specifica la colonna su cui si trova l'elemento.
16 Ritorno a capo riga dopo la stampa di una riga della matrice in modo che i valori stampati assumano l'aspetto della matrice.
Commenti.
Se non vengono previsti gli opportuni ritorni a capo alla fine di ogni riga, i valori vengono stampati per righe ma tutti uno di seguito all'altro. Per facilitare l'inserimento dei dati, anche le operazioni di lettura possono essere combinate con operazioni di posizionamento a capo e spaziature, in modo che anche i dati inseriti assumano un aspetto tabellare.
ESEMPIO 35
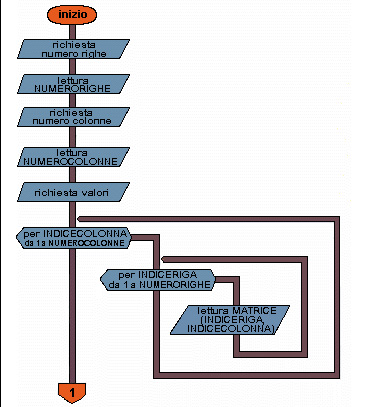
Lettura e stampa per colonne di una matrice. Volendo trattare la matrice per colonne, bisogna invertire i cicli, considerando in quello più interno l'indice di riga e nel ciclo più esterno l'indice di colonna. Fissato l'indice di colonna, viene letta la prima colonna, facendo variare l'indice di riga; poi si incrementa l'indice di colonna e si legge la colonna successiva, facendo nuovamente variare l'indice di riga e così via, finché si esauriscono le colonne. In modo analogo viene eseguita la scrittura per colonne. Ovviamente è impossibile, scrivendo la matrice per colonne, ottenere una tabella di aspetto identico a quella di partenza:
infatti i dati vengono scritti uno alla volta e il carrello della stampante dovrebbe posizionarsi indietro di alcune righe per ogni nuova colonna (può essere possibile sul video usando opportune istruzioni di posizionamento del cursore). Si possono quindi ottenere i valori per colonne uno di seguito all'altro o uno sotto l'altro o ottenere una tabella in cui ogni riga è formata da una delle colonne della matrice di partenza. Negli esempi proposti si segue l'ultimo metodo: si ottiene una tabella in cui ogni riga è formata da una delle colonne della matrice di partenza, inserendo un ritorno a capo dopo la stampa di ciascuna colonna.
Flow chart Esempio 35 (prima parte)
Flow chart Esempio 35 (seconda parte)
Pseudocodifica (vedi Figure)
1 inizio
2 emissione richiesta numero righe
3 lettura NUMERORIGHE
4 emissione richiesta numero colonne
5 lettura NUMEROCOLONNE
6 emissione richiesta valori
7 per INDICECOLONNA da 1 a NUMEROCOLONNE con passo 1
8 per INDICERIGA da 1 a NUMERORIGHE con passo 1
9 lettura MATRICE(INDICERIGA, INDICECOLONNA)
10 fine per
11 fine per
12 per INDICECOLONNA da 1 a NUMEROCOLONNE con passo 1
13 per INDICERIGA da 1 a NUMERORIGHE con passo 1
14 emissione MATRICE (INDICERIGA, INDICECOLONNA)
15 fine per
16 ritorno a capo riga
17 fine per
18 fine
2-3
Richiesta del numero di righe utilizzate della matrice.
4-5 Richiesta del numero di colonne utilizzate della matrice.
da 7 a 11 Inserimento dei valori nella matrice;
vengono usati due cicli FOR nidificati.
7 Il ciclo FOR più esterno viene ripetuto per un numero di volte pari a NUMEROCOLONNE cioè al numero di colonne utilizzate;
ad ogni ciclo viene incrementata la variabile INDICECOLONNA.
8 Il ciclo FOR più interno viene ripetuto per un numero di volte pari a NUMERORIGHE, cioè al numero di righe utilizzate, per ogni valore di INDICECOLONNA;
ad ogni ciclo viene incrementata la variabile INDICERIGA.
9 Lettura di un elemento della matrice;
l'elemento viene individuato dagli indici, cioè dai valori di INDICERIGA, che specifica la riga su cui si trova l'elemento, e INDICECOLONNA, che specifica la colonna su cui si trova l'elemento.
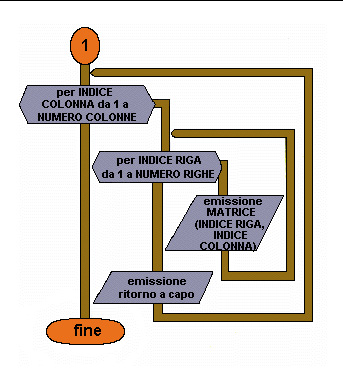
da 12 a 17 Stampa della matrice;
vengono usati due cicli FOR nidificati.
Anche in questo caso nel ciclo FOR più esterno varia l'indice di colonna e nel ciclo più interno l'indice di riga.
14 Stampa di un elemento della matrice;
l'elemento viene individuato dagli indici, cioè dai valori di INDICERIGA, che specifica la riga su cui si trova l'elemento, e INDICECOLONNA, che specifica la colonna su cui si trova l'elemento.
16 Ritorno a capo riga dopo la stampa di una colonna della matrice;
non si riesce ad ottenere la matrice come realmente si presenta.
ESEMPIO 36 Lettura per righe e stampa per colonne di una matrice.
Flow chart Esempio 36 (prima parte)
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
Flow chart Esempio 36 (seconda parte)
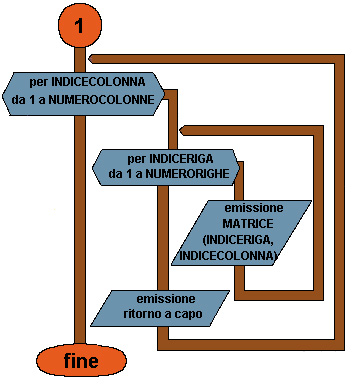
Pseudocodifica
1 inizio
2 emissione richiesta numero righe
3 lettura NUMERORIGHE
4 emissione richiesta numero colonne
5 lettura NUMEROCOLONNE
6 emissione richiesta valori
7 per INDICERIGA da 1 a NUMERORIGHE con passo 1
8 per INDICECOLONNA da 1 a NUMEROCOLONNE con passo 1
9 lettura MATRICE(INDICERIGA, INDICECOLONNA)
10 fine per
11 fine per
12 per INDICECOLONNA da 1 a NUMEROCOLONNE con passo 1
13 per INDICERIGA da 1 a NUMERORI- GHE con passo 1
14 emissione MATRICE (INDICERIGA, INDICECOLONNA)
15 fine per
16 ritorno a capo riga
17 fine per
18 fine
da 7 a 11
Per leggere la matrice per righe nel ciclo FOR più esterno varia l'indice di riga e nel ciclo FOR più interno varia l'indice di colonna.
da 12 a 17
Per stampare la matrice per colonne nel ciclo FOR più esterno varia l'indice di colonna e nel ciclo FOR più interno varia l'indice di riga.
ESEMPIO 37 Lettura per colonne e stampa per righe di una matrice.
Flow chart Esempio 37 (prima parte)
Flow chart Esempio 37 (seconda parte)
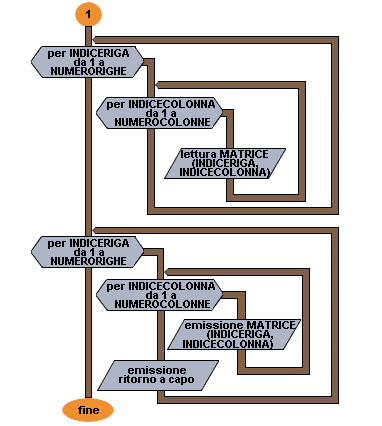
Pseudocodifica (vedi Figure)
1 inizio
2 emissione richiesta numero righe
3 lettura NUMERORIGHE
4 emissione richiesta numero colonne
5 lettura NUMEROCOLONNE
6 emissione richiesta valori
7 per INDICECOLONNA da 1 a NUMEROCOLONNE con passo 1
8 per INDICERIGA da 1 a NUMERORIGHE con passo 1
9 lettura MATRICE(INDICERIGA, INDICECOLONNA)
10 fine per
11 fine per
12 per INDICERIGA da 1 a NUMERORIGHE con passo 1
13 per INDICECOLONNA da 1 a NUMEROCOLONNE con passo 1
14 emissione MATRICE (INDICERIGA, INDICECOLONNA)
15 fine per
16 ritorno a capo riga
17 fine per
18 fine
da 7 a 11
Per leggere la matrice per colonne nel ciclo FOR più esterno varia l'indice di colonna e nel ciclo FOR più interno varia l'indice di riga.
da 12 a 17
Per stampare la matrice per righe nel ciclo FOR più esterno varia l'indice di riga e nel ciclo FOR più interno varia l'indice di colonna.
LA MATRICE TRASPOSTA
La matrice che si ottiene stampando ogni colonna su una riga (o viceversa) si dice matrice trasposta. Se la matrice è quadrata, cioè il numero di righe è uguale a quello delle colonne è possibile ottenere la matrice trasposta sulla matrice iniziale, scambiando in modo simmetrico gli elementi rispetto alla diagonale (cioè rispetto agli elementi in cui l'indice di riga è uguale all'indice di colonna).LE OPERAZIONI SULLE MATRICI
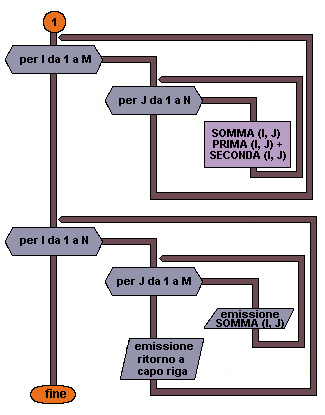
Sulle matrici con elementi di tipo numerico sono definite alcune operazioni, come il prodotto per uno scalare (cioè per un numero), la somma di due matrici e il prodotto. - prodotto di una matrice per uno scalare: Il prodotto di una matrice per uno scalare viene eseguito moltiplicando ciascuna componente della matrice per un valore scalare. - somma di due matrici: La somma di due matrici può essere effettuata soltanto tra matrici con le stesse dimensioni: stesso numero di righe e stesso numero di colonne; la matrice somma mantiene le stesse dimensioni. La somma è definita componente per componente; ogni elemento della matrice somma è il risultato della somma dei corrispondenti elementi delle matrici di partenza. - moltiplicazione di due matrici La moltiplicazione è definita tra due matrici A e B se il numero delle colonne di A è uguale al numero delle righe di B. Sia A una matrice di dimensione M x K e B una matrice di dimensione K x N. Il prodotto delle due matrici dà come risultato una matrice di dimensione M x N in cui ogni elemento i,j è il risultato del prodotto scalare della i-esima riga della matrice A per la J-esima colonna della matrice B (ogni riga e colonna, fissato un indice può essere vista come un vettore).ESEMPIO 38 Somma di due matrici di dimensioni M x N (M righe e N colonne). Anche la matrice somma deve avere dimensioni M x N. Descrizione delle variabili:
Flow chart Esempio 38 (prima parte)
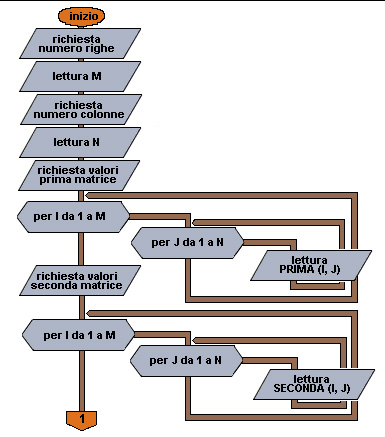
Flow chart Esempio 38 (seconda parte)
Pseudocodifica (vedi Figure)
1 inizio
2 emissione richiesta numero righe
3 lettura M
4 emissione richiesta numero colonne
5 lettura N
6 emissione richiesta valori prima matrice
7 per I da 1 a M con passo 1
8 per J da 1 a N con passo 1
9 lettura PRIMA(I, J)
10 fine per
11 fine per
12 emissione richiesta valori seconda matrice
13 per I da 1 a M con passo 1
14 per J da 1 a N con passo 1
15 lettura SECONDA(I, J)
16 fine per
17 fine per
18 per I da 1 a M con passo 1
19 per J da 1 a N con passo 1
20 SOMMA(I, J) = PRIMA(I, J) + SECONDA(I, J)
21 fine per
22 fine per
23 per I da 1 a M con passo 1
24 per J da 1 a N con passo 1
25 emissione SOMMA(I, J)
26 fine per
27 ritorno a capo riga
28 fine per
29 fine
2-3
Richiesta del numero di righe utilizzate delle matrici.
4-5 Richiesta del numero di colonne utilizzate delle matrici.
da 7 a 11
Inserimento dei valori nella prima matrice.
da 13 a 17
Inserimento dei valori nella seconda matrice.
da 18 a 22
Somma delle due matrici; la somma viene eseguita elemento per elemento utilizzando due cicli FOR per scorrerli tutti.
20
Somma degli elementi corrispondenti della prima e della seconda matrice e assegnazione del risultato all'elemento corrispondente della matrice somma.
da 23 a 28
Stampa della matrice risultato.
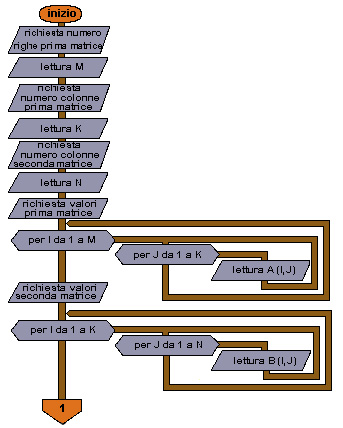
ESEMPIO 39
Moltiplicazione di due matrici (la prima di dimensioni M x K;
la seconda di dimensioni K x N).
Il prodotto scalare della i-esima riga di A per la j-esima colonna di B fissati i e j diventa:
SOMMA = 0 per H da 1 a K con passo 1
SOMMA = SOMMA + A(I, H) * B(H, J) fine per
Ogni prodotto di questo tipo fornisce un elemento della matrice prodotto che ha dimensione M x N;
quindi per calcolare tutti gli elementi si deve fare un ciclo sugli elementi della matrice prodotto.
Descrizione delle variabili:
Flow chart Esempio 39 (prima parte)
Flow chart Esempio 39 (seconda parte)
Pseudocodifica (vedi Figure)
1 inizio
2 emissione richiesta numero righe prima matrice
3 lettura M
4 emissione richiesta numero colonne prima matrice e righe seconda matrice
5 lettura K
6 emissione richiesta numero colonne seconda matrice
7 lettura N
8 emissione richiesta valori prima matrice
9 per I da 1 a M con passo 1
10 per J da 1 a K con passo 1
11 lettura A(I, J)
12 fine per
13 fine per
14 emissione richiesta valori seconda matrice
15 per I da 1 a K con passo 1
16 per J da 1 a N passo 1
17 lettura B(I, J)
18 fine per
19 fine per
20 per I da 1 a M con passo 1
21 per J da 1 a N con passo 1
22 C(I, J) = 0
23 per H da 1 a K con passo 1
24 C(I,J) = C(I,J) + A(I, H) * B(H, J)
25 fine per
26 fine per
27 fine per
28 per I da 1 a M con passo 1
29 per J da 1 a N con passo 1
30 emissione C(I, J)
31 fine per
32 ritorno a capo riga
33 fine per
34 fine
2-3
Richiesta del numero di righe della prima matrice utilizzate.
4-5
Richiesta del numero di colonne della prima matrice utilizzate;
deve essere uguale al numero di righe della seconda matrice perché sia definita l'operazione di moltiplicazione.
6-7
Richiesta del numero di colonne della seconda matrice utilizzate.
da 9 a 13
Inserimento dei valori nella prima matrice.
da 15 a 19
Inserimento dei valori nella seconda matrice.
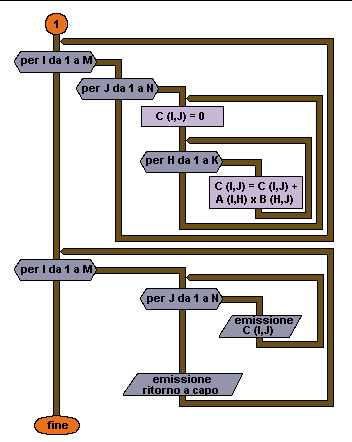
da 20 a 27
Moltiplicazione delle due matrici.
20-21
Il ciclo viene fatto sugli elementi della matrice risultato;
per ogni elemento viene calcolato il risultato del prodotto scalare di una riga della prima matrice per una colonna della seconda matrice.
22
Azzeramento di un elemento della matrice risultato;
è necessario perché poi questo elemento viene usato nel calcolo del prodotto scalare.
da 23 a 25
Ciclo per il calcolo del prodotto scalare della riga I della prima matrice per la colonna J della seconda matrice.
da 28 a 33 Stampa della matrice risultato.
![]()
GESTIONE DI ELEMENTI IN MODO CASUALE
E' possibile riferirsi ad un elemento qualsiasi della matrice specificandone gli indici. Per esempio è possibile inserire un valore in un elemento qualsiasi della matrice, o richiedere la stampa di un elemento qualunque, o incrementarne il valore, specificando gli indici che identificano l'elemento.![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Dizionario Storia Antica e Medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()











