Ripasso di Matematica per l'informatica
Informatica Programmazione
Le Strutture Cicliche Le Matrici Dall'Algoritmo al Programma I Files I Primi Elementi I Vettori Il Controllo degli Errori La Grafica L'Analisi Top Down Programmazione RAD
Web link:
Rai Play Informatica Scuola Programmazione Cultura
Strutture Iterative while for do C++
Programmazione C Ciclo Pre-condizionale (while)
Programmazione La Struttura Condizionale
Esempio 5 Il programma riceve i nomi di due persone e li riscrive in ordine alfabetico
Struttura condizionale con un solo ramo
Strutture condizionali in sequenza e nidificate
Esempio 6 Il programma stabilisce in quale giorno della settimana cade un qualsiasi giorno dell'anno
Flow chart esempio 6 (prima parte) Flow chart Esempio 6 (seconda parte)
Esempio 7 Il programma richiede i nomi e le date di nascita di due persone poi ...
Flow chart esempio 7 (prima parte) Flow chart Esempio 7 (seconda parte)
Algebra di Boole della logica proporzionale
Strutture condizionali in sequenza, nidificate, o condizioni composte?
Esempio 8 Il programma deve stabilire se una lettera inserita è una vocale o una consonante
Flow chart esempio 8a (prima parte) Flow chart esempio 8a (seconda parte) Flow chart esempio 8b Flow chart Esempio 8c
Trace con strutture condizionali
LA STRUTTURA CONDIZIONALE
Utilizzando soltanto la struttura sequenziale l'algoritmo ha un processo di esecuzione fisso; cioè le istruzioni che lo compongono vengono tutte eseguite una dopo l'altra sempre allo stesso modo.Spesso è necessario rendere l'algoritmo variabile, cioè poter eseguire istruzioni diverse in base al verificarsi di un certo evento.
La struttura condizionale permette di eseguire due diverse sequenze di istruzioni, in alternativa, secondo il valore di una determinata condizione.
Le due sequenze di istruzioni in alternativa compongono i due "rami" della struttura condizionale.
La condizione è una proposizione logica che può assumere uno dei valori di verità Vero o Falso.
Può essere costituita dal confronto tra due variabili numeriche, o tra una variabile e una costante per determinare, per esempio, se sono uguali o diverse, o se una è maggiore dell'altra, o se, tra due parole, una precede l'altra nell'ordine alfabetico ecc.
Lo schema generale della struttura condizionale è:
se condizione allora istruzioni A altrimenti istruzioni B fine se
Se la proposizione logica che costituisce la condizione ha valore Vero vengono eseguite le istruzioni indicate come istruzioni A, altrimenti se ha valore Falso, vengono eseguite le istruzioni indicate come istruzioni B.
ESEMPIO 5
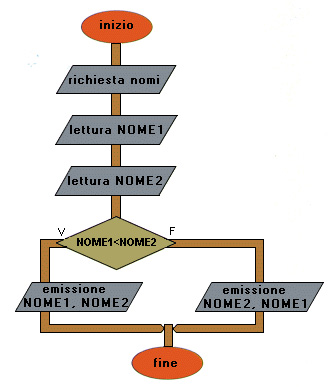
Questo programma riceve i nomi di due persone e li riscrive in ordine alfabetico.
Descrizione delle variabili.
Pseudo codifica (vedi Figura)
1 inizio
2 emissione richiesta nomi
3 lettura NOME1
4 lettura NOME2
5 se NOME1 NOME2 allora
6 emissione NOME1, NOME2
7 altrimenti
8 emissione NOME2, NOME1
9 fine se
10 fine 3-4
Inserimento dei due nomi,
in ordine qualsiasi (per nome si intende anche cognome e nome separati da spazi).
Da 5 a 9 struttura condizionale per la stampa dei nomi in ordine alfabetico.
5 Confronto tra le variabili che contengono i nomi; il simbolo "" in questo caso significa "precede nell'ordine alfabetico".
6 Se la condizione è vera, cioè NOME1 precede NOME2 nell'ordine alfabetico, viene stampato prima NOME1 e poi NOME2.
8 Se la condizione è falsa, viene stampato prima NOME2 e poi NOME1.
Commenti.
Il confronto tra variabili alfanumeriche nei linguaggi di programmazione avviene in base al codice ASCII corrispondente a ciascun carattere.
In questo esempio ogni ramo della struttura condizionale contiene una sola istruzione, ma in generale i rami delle strutture condizionali possono contenere una sequenza di istruzioni (di qualsiasi tipo).
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
STRUTTURA CONDIZIONALE CON UN SOLO RAMO
La struttura condizionale può essere costituita da un solo ramo se per uno dei due valori della condizione non deve essere eseguita nessuna istruzione.se condizione allora istruzioni A fine
se oppure se non condizione allora istruzioni B fine
se
STRUTTURE CONDIZIONALI IN SEQUENZA E NIDIFICATE
Le strutture condizionali possono essere combinate in vario modo tra loro o con altre strutture di controllo per la soluzione di un problema.Se una struttura condizionale inizia dopo la conclusione della precedente si parla di strutture in sequenza.
Si hanno invece strutture condizionali nidificate se un ramo di una struttura condizionale contiene a sua volta un'altra struttura condizionale.
Possono esserci anche più livelli di nidificazione.
ESEMPI.
Ecco due esempi di strutture condizionali nidificate; nel secondo esempio si nota che anche strutture condizionali nidificate possono avere un solo ramo.
se condizione 1 allora se condizione 2 allora istruzioni A altrimenti se condizione 3 allora istruzioni B altrimenti istruzioni C fine se fine se altrimenti istruzioni D fine se se condizione 1 allora se condizione 2 allora se non condizione 3 allora istruzioni A fine se altrimenti istruzioni B fine se fine se
ESEMPIO 6
Questo programma stabilisce in quale giorno della settimana cade un qualsiasi giorno dell'anno, individuato da un numero compreso tra 1 e 365, sapendo qual'è il primo giorno dell'anno (per esempio martedì).
Per individuare il giorno della settimana in base al numero, basta tener presente che, se per ipotesi il giorno 1 è martedì, sarà martedì ogni 7 giorni, cioè il giorno 8, il giorno 15, il giorno 22 ecc., cioè ogni volta che il numero è un multiplo di 7 più 1; se il giorno 2 è mercoledì lo sarà anche il giorno 9, il giorno 16, il giorno 23 ecc, cioè ogni volta che il numero è un multiplo di 7 più 2. Così sarà giovedì ogni volta che il numero è un multiplo di 7 più 3, venerdì se il numero è un multiplo di 7 più 4, sabato se è un multiplo di 7 più 5, domenica se è un multiplo di 7 più 6, lunedì se è esattamente un multiplo di 7 (un multiplo di 7 più 7 è ancora un multiplo di 7).
Per risolvere il problema basta allora calcolare il resto della divisione per 7 del numero inserito; il resto è un numero compreso tra 0 e 6 che permette di individuare facilmente il giorno della settimana.
Descrizione delle variabili.
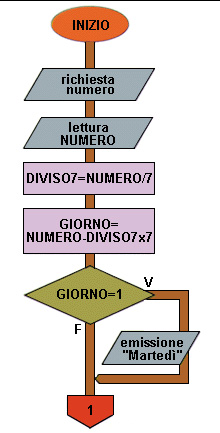
Flow chart Esempio 6 (prima parte)
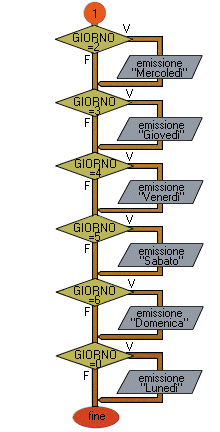
Flow chart Esempio 6 (seconda parte)
Pseudo codifica (vedi Figure)
1 inizio
2 emissione richiesta numero (tra 1 e 365)
3 lettura NUMERO
4 DIVISO7 = NUMERO / 7
5 GIORNO = NUMERO - DIVISO7 X 7
6 se GIORNO = 1 allora
7 emissione "Martedì"
8 fine se
9 se GIORNO = 2 allora
10 emissione "Mercoledì"
11 fine se
12 se GIORNO = 3 allora
13 emissione "Giovedì"
14 fine se
15 se GIORNO = 4 allora
16 emissione "Venerdì"
17 fine se
18 se GIORNO = 5 allora
19 emissione "Sabato"
20 fine se
21 se GIORNO = 6 allora
22 emissione "Domenica"
23 fine se
24 se GIORNO = 0 allora
25 emissione "Lunedì"
26 fine se
27 fine
3 Inserimento del numero che deve essere compreso tra 1 e 365 (o 366 se l'anno è bisestile).
4-5 Calcolo del resto della divisione per 7 (tenendo presente che NUMERO = (NUMERO/7)x7 + RESTO se nella divisione per 7 viene considerata solo la parte intera.
Da 6 a 26 strutture condizionali che permettono di individuare il giorno della settimana.
Tutti i casi si escludono a vicenda; è possibile quindi utilizzare una serie di strutture condizionali in sequenza.
Commenti L'output di questo programma non comprende variabili ma soltanto le costanti corrispondenti ai nomi dei giorni della settimana.
ESEMPIO 7
Questo programma richiede i nomi e le date di nascita di due persone; permette poi, a richiesta, di ottenere i dati delle due persone in ordine alfabetico in base al nome, o in ordine di età.
Descrizione delle variabili.
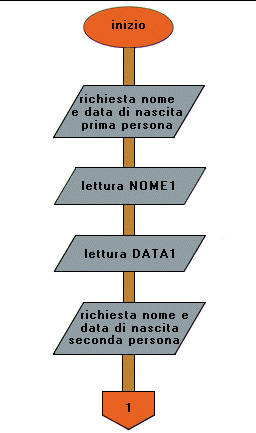
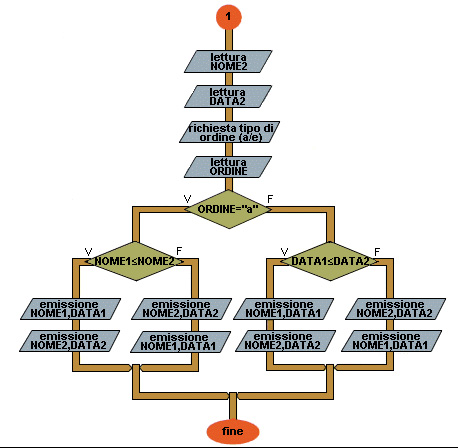
Flow chart Esempio 7 (prima parte)
Flow chart Esempio 7 (seconda parte)
Pseudo codifica (vedi Figure)
1 inizio
2 emissione richiesta nome e data di nascita prima persona
3 lettura NOME1
4 lettura DATA1
5 emissione richiesta nome e data di nascita seconda persona
6 lettura NOME2
7 lettura DATA2
8 richiesta tipo di ordine (a/e)
9 lettura ORDINE
10 se ORDINE = "a" allora (ordine alfabetico)
11 se NOME1 _ NOME2 allora
12 emissione NOME1, DATA1
13 emissione NOME2, DATA2
14 altrimenti
15 emissione NOME2, DATA2
16 emissione NOME1, DATA1
17 fine se
18 altrimenti (ordine di età)
19 se DATA1 _ DATA2 allora
20 emissione NOME1, DATA1
21 emissione NOME2, DATA2
22 altrimenti
23 emissione NOME2, DATA2
24 emissione NOME1, DATA1
25 fine se
26 fine se
27 fine 3 e 6 Inserimento dei nomi (anche cognome e nome).
4 e 8 Inserimento delle date di nascita;
perché si possa fare direttamente il confronto tra le date, queste devono essere inserite nel formato anno, mese, giorno.
L'anno può essere inserito con quattro cifre o con due cifre a scelta, ma nello stesso formato per le due date.
9 Inserimento della scelta tra ordine alfabetico e ordine di età; bisogna inserire uno dei caratteri "a" (per alfabetico) o "e" (per età).
Un carattere diverso farebbe comunque ottenere l'ordinamento in base all'età poiché la condizione alla riga 10 risulterebbe falsa e verrebbero eseguite le istruzioni del ramo falso.
Da 10 a 26 struttura condizionale per l'ordinamento in base all'ordine alfabetico o all'età;
se è stato inserito il carattere "a" vengono eseguite le istruzioni dalla 11 alla 17, altrimenti le istruzioni dalla 19 alla 25.
Da 11 a 17 struttura condizionale per la stampa dei dati in ordine alfabetico in base al confronto tra i nomi.
Da 19 a 25 struttura condizionale per la stampa dei dati in ordine di età in base al confronto tra le date di nascita.
Commenti.
DATA1 e DATA2 potrebbero essere anche numerici, ma se definiti interi si verifica un overflow (essendo 32767 il numero intero più grande ammesso, mentre una data è di almeno 6 cifre e quindi più grande).
Nello stabilire il test della struttura condizionale bisogna fare particolarmente attenzione ai casi limite;e;
per esempio nel confronto di due valori si distinguono i casi:
- primo valore maggiore del secondo;
- secondo valore maggiore del primo;
- valori uguali (caso limite).
In questo esempio se due valori (nomi o data) sono uguali, si vogliono stampare i dati nell'ordine in cui sono stati inseriti, quindi il test va fatto per minore o uguale e non solo per minore.
Nell'esempio precedente, invece, se i nomi erano uguali era indifferente stampare prima il primo o il secondo.
CONDIZIONI COMPOSTE
I test delle strutture condizionali possono essere condizioni composte con operatori logici.La condizione composta viene valutata per stabilirne il valore di verità (Vero o Falso) in base ai valori delle condizioni semplici e agli operatori da applicare.
OPERATORI LOGICI
Gli operatori logici più comuni sono AND, OR e NOT;il loro comportamento è definito da tabelle, dette tavole di verità, in cui ad ogni possibile coppia di valori (Vero o Falso) degli operandi viene associato il valore (Vero o Falso) del risultato delle operazioni.
Le tavole di verità per gli operatori OR, AND e NOT sono:
ALGEBRA DI BOOLE DELLA LOGICA PROPORZIONALE
Un'algebra booleana è una sestupla < B + * - 0 1 > dove B è un insieme di due o più elementi sul quale è definita una relazione di uguaglianza (=) riflessiva, simmetrica e transitiva, nel quale valgono alcune particolari proprietà per le operazioni.Gli elementi dell'algebra possono essere di qualsiasi natura e i simboli 0 e 1 usati per indicare gli elementi neutri indicano due di tali elementi (non hanno relazione con i numeri 0 e 1).
Così pure le operazioni + e * non sono necessariamente le operazioni di addizione e moltiplicazione tra numeri ma rappresentano due operazioni tra i dati che soddisfano le proprietà richieste.
Se l'insieme B contiene solo due elementi l'algebra si dice binaria.
L'insieme dei valori degli enunciati della logica proposizionale "Vero" e "Falso" su cui si definiscono le operazioni OR AND e NOT costituisce un'algebra di Boole binaria.
Una proposizione è una frase che può essere vera o falsa. Le proposizioni elementari possono essere combinate tra di loro in proposizioni composte mediante connettivi definiti tramite tabelle dette tavole di verità.
La sestupla corrisponde a B={Vero, Falso}, +=AND, *=OR, -=NOT, 0=Vero, 1=Falso. Per l'algebra delle proposizioni valgono le seguenti proprietà:
(A e B siano proposizioni aventi valori di verità Vero o Falso) P1) AND e OR sono operazioni commutative:
A and B = B and A A or B = B or A P2) e reciprocamente distributive:
A or (B and C) = (A or B) and (A or C) A and (B or C) = (A and B) or (A and C) P3)
Vero è un elemento neutro rispetto all'AND, cioè non muta il valore di una proposizione;
Falso è l'elemento neutro rispetto all'OR. A and Vero = A A or Falso = A P4)
NOT è un'operazione unaria (agisce su un solo operando) detta di negazione o complemento:
Il complemento di A è not(A) ed è tale che A or not(A) = Vero A and not(A) = Falso
Da queste si possono ricavare alcuni teoremi;
Teorema dell'involuzione: not(not(A)) = A
Teorema dell'esistenza di un elemento annullatore:
A and Falso = Falso A or Vero = Vero
Teorema della proprietà di assorbimento:
A or (A and B) = A A and (A or B) = A
Teorema della proprietà di idempotenza: A and A = A A or A = A
Teorema delle leggi di De Morgan:
not(A and B) = not(A) or not(B) not(A or B) = not(A) and not(B)
Teorema della proprietà di associatività di AND e OR:
(A and B) and C = A and (B and C) (A or B) or C = A or (B or C)
I postulati e i teoremi permettono di trasformare un'espressione booleana in un'altra forma equivalente.
STRUTTURE CONDIZIONALI IN SEQUENZA, NIDIFICATE, O CONDIZIONI COMPOSTE?
Per descrivere un algoritmo quando si possono usare strutture condizionali in sequenza e quando invece è necessario ricorrere a strutture condizionali nidificate o a condizioni composte?Per poter usare soltanto strutture condizionali in sequenza, le condizioni devono far riferimento a casi indipendenti l'uno dall'altro.
Se ciò non si verifica si dovranno usare strutture nidificate o si dovranno rendere indipendenti le condizioni individuando le condizioni composte che risolvono il problema.
ESEMPIO 8
Questo programma deve stabilire se una lettera inserita è una vocale o una consonante.
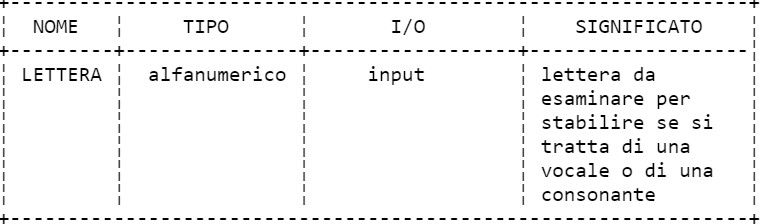
Descrizione delle variabili.
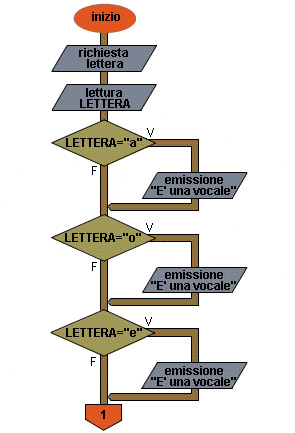
Flow chart Esempio 8a (prima parte)
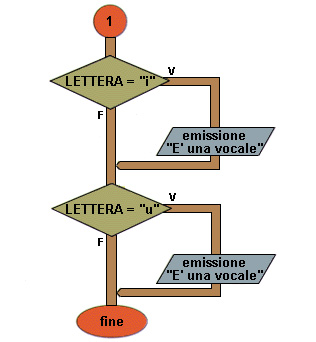
Flow chart Esempio 8a (seconda parte)
Pseudo codifica (vedi Figure)
1 inizio
2 richiesta lettera
3 lettura LETTERA
4 se LETTERA = "a" allora
5 emissione "E' una vocale"
6 fine se
7 se LETTERA = "o" allora
8 emissione "E' una vocale"
9 fine se
10 se LETTERA = "e" allora 11 emissione "E' una vocale"
12 fine se
13 se LETTERA = "i" allora
14 emissione "E' una vocale"
15 fine se
16 se LETTERA = "u" allora
17 emissione "E' una vocale"
18 fine se
19 fine
2-3 Inserimento della lettera da esaminare.
Da 4 a 18 ci sono cinque strutture condizionali, in sequenza, una per ogni vocale.
Pseudo codifica (vedi Figura)
1 inizio
2 richiesta lettera
3 lettura LETTERA
4 se LETTERA = "a" allora
5 emissione "E' una vocale"
6 altrimenti
7 se LETTERA = "o" allora
8 emissione "E' una vocale"
9 altrimenti
10 se LETTERA = "e" allora
11 emissione "E' una vocale"
12 altrimenti
13 se LETTERA = "i" allora
14 emissione "E' una vocale"
15 altrimenti
16 se LETTERA = "u" allora
17 emissione "E' una vocale"
18 altrimenti
19 emissione "E' una consonante"
20 fine se
21 fine se
22 fine se
23 fine se
24 fine se
25 fine
2-3 Inserimento della lettera da esaminare.
Da 4 a 24 strutture condizionali nidificate.
4 Questa struttura condizionale si chiude alla riga 24.
7 Questa struttura condizionale si chiude alla riga 23.
10 Questa struttura condizionale si chiude alla riga 22.
13 Questa struttura condizionale si chiude alla riga 21.
16 Questa struttura condizionale si chiude alla riga 20.
18 Questo caso esclude che la lettera inserita sia una vocale; infatti si arriva a questo punto solo seguendo il ramo falso di ognuna delle 5 strutture condizionali nidificate.
Commento L'utilizzo di condizioni composte nei test può evitare o almeno semplificare l'uso delle strutture nidificate.
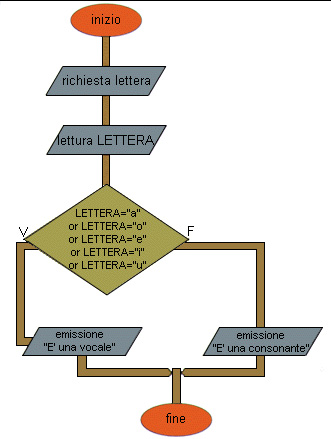
Pseudo codifica (vedi figura)
1 inizio
2 richiesta lettera
3 lettura LETTERA
4 se LETTERA = "a" or LETTERA = "o" or LETTERA = "e" or LETTERA = "i" or LETTERA = "u" allora
5 emissione "E' una vocale"
6 altrimenti
7 emissione "E' una consonante"
8 fine se
9 fine
2-3 Inserimento della lettera da esaminare.
4 Condizione composta;
le condizioni semplici vengono composte con l'operatore OR in quanto basta che una sola delle condizioni sia vera perché si possa stabilire che la lettera è una vocale;
(se le condizioni fossero composte con l'operatore AND quella composta non potrebbe mai avere valore Vero perché le diverse condizioni non possono essere vere contemporaneamente).
TRACE CON STRUTTURE CONDIZIONALI
Il comportamento errato di un programma con strutture condizionali può essere dovuto all'esecuzione di un ramo non corretto di una delle strutture.Può essere utile eseguire la trace del programma per individuare tale situazione;
per esempio:
- stampare prima dell'inizio della struttura condizionale il valore delle variabili che intervengono in modo da valutare la condizione verificata;
- porre in ogni ramo della struttura condizionale un messaggio che identifichi il ramo stesso (e quindi il tipo di condizione verificata).
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
