Ripasso di Matematica Geometria dello Spazio
Matematica Geometria Solida Nozioni Generali
Aritmetica Geometria Informatica
Dizionario Lessicale di Geometria
Geometria Piana e Solida Informatica Media
GEOMETRIA PIANA E SOLIDA
Geometria solida nozioni generali Elementi Fondamentali della Geometria Gli Angoli Il Triangolo Il Cerchio Linee sul Piano Quadrilateri e Poligoni Superficie dei Poligoni Cilindri e Prismi Coni e Piramidi Gli Esaedri La Sfera Geometria Solida Nozioni Generali Solidi di Rotazione
![]()
![]()
MATEMATICA GEOMETRIA SOLIDA - NOZIONI GENERALI
FIGURE SPAZIALI
Una figura geometrica i cui punti non giacciono tutti sullo stesso piano si chiama figura spaziale.La geometria solida o stereometria è la geometria che studia le figure spaziali.
POSIZIONI RELATIVE FRA RETTE E PIANI
Nello spazio due rette possono trovarsi nello stesso piano, e in questo caso possono essere parallele o incidenti. Se non si trovano sullo stesso piano esse si dicono sghembe, e in questo caso sono sempre situate su due piani paralleli. Una retta e un piano possono trovarsi nelle seguenti posizioni:I) la retta ha due punti A e B in comune con il piano: allora li ha in comune tutti e si dice che la retta «giace nel piano».
II) la retta ha un solo punto A in comune con il piano: in tal caso la retta si dice incidente al piano.
III) la retta non ha punti in comune con il piano: si dice allora che la retta è parallela al piano.
Un caso particolarmente importante è quello della retta perpendicolare al piano:
Una retta si dice perpendicolare a un piano quando è perpendicolare a tutte le rette passanti per il punto P di incidenza e giacenti nel piano.
Il punto P si chiama piede della perpendicolare.
Osserviamo che una retta perpendicolare a un piano è in ogni caso incidente a esso. Una retta incidente non perpendicolare si dice comunemente inclinata o obliqua rispetto al piano.
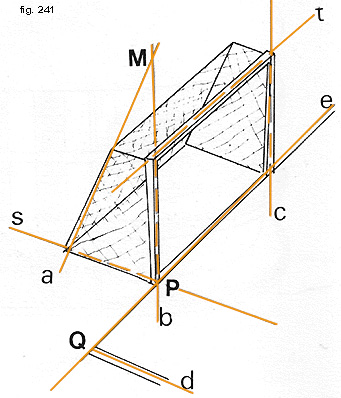
Vediamo di capire meglio questi concetti con un esempio familiare. Osserviamo la fig. 241: la retta «b», del palo sinistro è incidente alla «e» della linea di fondo: esse hanno in comune il piede P del palo; lo stesso vale per la «d», che è la linea che delimita l'area di rigore: esse si incontrano in Q. Anche la retta «a» del sostegno di rete è incidente alla «b», che incontra nel punto M al di sopra della traversa. Le rette «b» e «c» dei pali sono poi parallele e giacciono nel piano dello specchio di porta, cioè quel piano che il pallone deve oltrepassare per convalidare il goal.
![]()
![]()
La retta «a» è sghemba rispetto alla «e», alla «d», e alla retta della traversa «t»: quest'ultima è parallela al piano del tappeto erboso. La «a» infine è incidente al piano del campo ed obliqua, mentre la «b» è anche perpendicolare: infatti è perpendicolare tanto alla «s» quanto alla «e».
POSIZIONI RELATIVE FRA PIANI
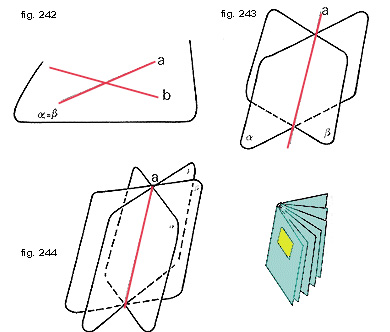
Due piani nello spazio possono avere:I) due rette in comune: in tal caso formano un unico piano e si dicono coincidenti (fig. 242).
II) una retta in comune: in questo caso si dicono secanti e la retta si chiama intersezione (fig. 243).
Molti piani secanti aventi la stessa intersezione formano un fascio di piani; la retta di intersezione prende il nome di sostegno del fascio (fig. 244).
III) nessuna retta in comune: qui i piani si dicono paralleli.
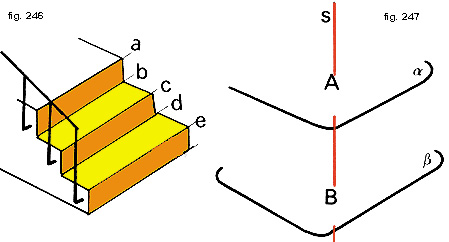
Osserviamo ora la fig. 246: i piani verticali di una scala si chiamano piani di alzata e sono tutti paralleli fra loro; allo stesso modo lo sono quelli orizzontali, detti piani di pedata. Le rette «a», «b», «c», ecc. sono gli spigoli degli scalini e sono tutte parallele. Ne possiamo trarre la seguente regola:
Le intersezioni di un piano con due o più piani paralleli sono rette parallele.
Un'altra importante proprietà dei piani paralleli è la seguente:
Se una retta è perpendicolare a un piano lo è a ogni altro parallelo a questo (fig. 247).
Il segmento AB prende il nome di distanza fra i piani a e b.
DISTANZA DA UN PIANO
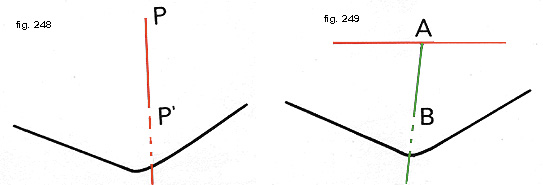
I) Distanza di un punto da un piano. Conducendo da un punto P esterno a un piano, cioè non appartenente al piano, la perpendicolare ad esso, lo si interseca nel punto P', detto piede o proiezione di P. Il segmento PP' rappresenta la distanza del punto P dal piano (fig. 248).II) Distanza di una retta da un piano.
Consideriamo una retta parallela a un piano (fig. 249): se da un suo punto A qualsiasi conduciamo la perpendicolare al piano, questa lo interseca in un punto B.
Chiameremo il segmento AB distanza della retta dal piano.
L'aereo supersonico Concorde sorvola l'Oceano Atlantico a più di 1.500 chilometri l'ora, a un'altezza di 10.000 metri.
Tale altezza rappresenta la distanza dell'aereo dal piano della superficie dell'oceano; la scia lasciata dal velivolo rappresenta la sua traiettoria ed è una retta la cui distanza da terra coincide con quella dell'aereo.
ANGOLI DIEDRI
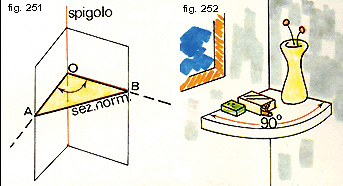
Due semipiani aventi una retta in comune dividono lo spazio in due parti dette diedri (fig. 251). I due semipiani rappresentano le facce mentre la retta comune si chiama spigolo. Secando il diedro con un piano perpendicolare allo spigolo si ottiene la sezione normale del diedro, la quale non è altro che l'angolo AôB. Osservando attentamente la fig. 252 ci rendiamo conto che l'angolo di una stanza è più esattamente un diedro e la mensola è la sua sezione normale.Dei due diedri in cui risulta diviso lo spazio, quello maggiore prende il nome di diedro concavo, quello minore di diedro convesso.
In una casa la zona al coperto è un diedro convesso, la parte allo scoperto è un diedro concavo.
Per i diedri valgono tutte le operazioni e le definizioni date per gli angoli allorché si considerino le loro sezioni normali: ad esempio se la sezione normale di un diedro misura 30° diremo che il diedro è di 30°. Allo stesso modo un diedro di 40° è la somma di due diedri di 15° e 25°.
Si dicono infine perpendicolari due piani quando intersecandosi formano quattro diedri retti. In un campo da tennis, ad esempio, il piano della rete è perpendicolare al piano di gioco.
SUPERFICI NELLO SPAZIO
Prendiamo la buccia di un'arancia e cerchiamo di spianarla su una tavola:essa si deformerà certamente e potrà spezzarsi.
Per quanto è stato detto all'inizio del capitolo essa non è dunque una figura piana, e poiché ha un'estensione ed è quindi una superficie, la chiameremo superficie spaziale.
Guardandoci attorno ci rendiamo subito conto che quasi tutte le superfici reali sono spaziali, a cominciare da quella del nostro pianeta, costituita da pianure (superfici piane) ma anche da colline e montagne (superfici spaziali).
Persino la superficie del mare, che è piana quando è calma, diventa spaziale quando è scossa dalla tempesta.
Consideriamo ora due tipi di superfici spaziali molto importanti dal punto di vista geometrico.
I) Superficie cilindrica
Data una linea piana qualsiasi «s» appartenente al piano a, si chiama superficie cilindrica quella formata da tutte le rette perpendicolari ad a passanti per i punti P 1, P 2, P 3, P 4 ... della linea «s».
Tali rette prendono il nome di generatrici, mentre la linea «s» si chiama direttrice.
Ad esempio una matita tenuta in posizione verticale muovendosi lascia una traccia sul foglio (direttrice) e genera una superficie cilindrica.
Se una superficie cilindrica ha per direttrice un poligono, essa prende il nome di prisma indefinito.
II) Superficie conica
Data una linea piana qualsiasi «s» appartenente al piano a , si chiama superficie conica quella formata da tutte le rette passanti per i punti P 1, P 2, P 3, P 4.. della linea «s» e per un punto V esterno ad a .
Il punto V è detto vertice, le rette generatrici, mentre la «s» si chiama direttrice.
Se una superficie conica ha per direttrice un poligono essa prende il nome di angoloide.
LINEE NELLO SPAZIO
Se osserviamo una strada che si inerpica sulla collina.Essa è una generica linea curva, ma non è piana:
infatti tutti i suoi punti, ad esempio i paracarri che la limitano, giacciono sul terreno, che è una superficie spaziale.
Se immaginiamo la strada come una linea, chiameremo quest'ultima linea spaziale.
La traiettoria delle astronavi Terra-Luna costituiscono un altro esempio di linea spaziale.
Molto importante, infine, per le sue proprietà geometriche, è l'elica cilindrica, così chiamata perché giace su una superficie cilindrica.
L'uso di questa linea spaziale nella tecnica è frequentissimo (scale a chiocciola, cavaturaccioli, molle,...).
SOLIDI
Diamo subito la seguente definizione:Si dice figura solida o semplicemente solido una porzione di spazio racchiusa da una superficie.
In tal modo i punti dello spazio si dividono in due:
quelli all'interno della superficie, che quindi fanno parte del solido, come A, B, C, e quelli all'esterno di essa, come D, E, F.
La massa di gas più leggero dell'aria, che consente a una mongolfiera di innalzarsi, rappresenta un esempio di solido, modellato dalla superficie del pallone.
Lo spazio occupato dal gas si chiama volume, mentre la membrana del pallone costituisce la superficie del solido.
Acquistando un litro di latte capita che questo sia confezionato in recipienti di diversa forma;
tuttavia la quantità contenuta in ciascuno di essi è sempre la stessa: le confezioni hanno cioè lo stesso volume:
di diverso c'è solo la superficie che lo racchiude.
Chiameremo quindi equivalenti questi solidi enunciando la seguente regola generale:
Due o più solidi si dicono equivalenti quando hanno lo stesso volume.
Il «palmer» di una bicicletta da corsa racchiude il volume d'aria necessario a ottenere una certa pressione per una marcia regolare;
in caso di forature, però, si affloscia e svuotandosi perde il volume, pur mantenendo la stessa superficie.
Ebbene, il pneumatico gonfiato e quello sgonfio rappresentano due solidi che hanno diverso volume ma uguale superficie.
Possiamo concludere con la seguente regola:
Due solidi si dicono uguali quando hanno lo stesso volume e la stessa superficie.
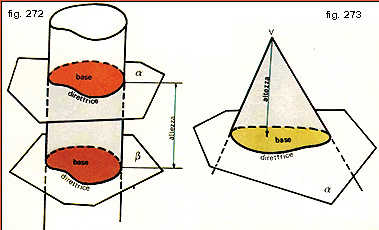
Vediamo adesso alcuni solidi notevoli per le loro proprietà geometriche. Consideriamo una superficie cilindrica avente per direttrice una linea chiusa e seghiamola con due piani paralleli (fig. 272). Le porzioni dei due piani racchiuse dalla direttrice sono uguali e prendono il nome di basi; il solido racchiuso fra le due basi e la parte di superficie cilindrica compresa fra quelle prende il nome di cilindro. Superficie laterale definiremo quella che fa parte della superficie cilindrica originaria. Chiameremo infine altezza la distanza fra i piani a e b.
Un altro solido importante si può ottenere segando con un piano una superficie conica avente una linea chiusa come direttrice: la parte di piano racchiusa dalla direttrice prende il nome di base e la parte di superficie conica che rimane dalla parte del vertice superficie laterale. Definiamo cono il solido racchiuso dalla base e dalla superficie laterale (fig. 273); chiameremo infine altezza la distanza fra il vertice e il piano a.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
POLIEDRI
Quando la superficie che racchiude un solido è formata da parti di superficie piana chiameremo questo con il nome di poliedro.Più precisamente:
Un poliedro è un solido limitato da una superficie costituita da poligoni appartenenti a piani diversi e aventi in comune a due a due un lato.
Vertici, spigoli e facce del poliedro vengono chiamati rispettivamente i vertici dei poligoni, i loro lati e i poligoni stessi.
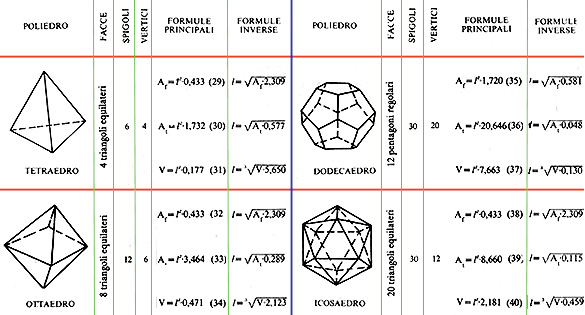
Il nome che si dà a un poliedro dipende dal numero delle facce che non possono mai essere meno di quattro: tetraedri, esaedri, ottaedri, rappresentano rispettivamente poliedri con quattro, sei e otto facce.
I segmenti che collegano vertici appartenenti a facce diverse si dicono diagonali.
La superficie di un poliedro gode sempre dell'importante proprietà di essere sviluppabile:
si può cioè ritagliarla opportunamente lungo gli spigoli in modo da stenderla su un piano e quindi misurarla.
La figura che si ottiene si chiama sviluppo del solido.
In geometria piana abbiamo definito regolari quei poligoni aventi i lati e gli angoli uguali.
Anche per i poliedri possiamo dare una definizione simile, e precisamente:
Dicesi regolare un poliedro avente facce e diedri tutti uguali.
Si potrebbe dimostrare che se i diedri e le facce sono uguali queste ultime sono necessariamente costituite da poligoni regolari.
In altre parole, se un poliedro è regolare le sue facce sono costituite da poligoni regolari.
La fig. 279 rappresenta tutti i poliedri regolari esistenti a eccezione del cubo.
VERO O FALSO?
1) Due rette che non hanno punti in comune sono sempre sghembe.2) Una retta incidente a un piano è sempre obliqua rispetto ad esso.
3) Due piani sono paralleli se non hanno punti in comune.
4) Due piani perpendicolari possono essere paralleli a una stessa retta.
5) La distanza di un punto da un piano si misura sulla perpendicolare a quest'ultimo.
6) La sezione normale di un diedro è la retta comune ai due suoi semipiani.
7) Le generatrici di una superficie cilindrica sono parallele.
8) Le generatrici di una superficie conica non hanno punti in comune.
9) L'angoloide è un caso particolare di superficie cilindrica.
10) Due solidi equivalenti hanno la stessa superficie.
11) La superficie di un poliedro è sempre sviluppabile.
1) Falso: possono essere anche parallele.
2) Falso: può essere anche perpendicolare.
3) Vero.
4) Vero.
5) Vero.
6) Falso: è il piano perpendicolare ad essa; la retta si chiama spigolo.
7) Vero.
8) Falso: passano tutte per il vertice.
9) Falso: è un caso particolare di superficie conica.
10) Falso: hanno lo stesso volume.
11) Vero.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()