![]()
News notizie del giorno Online Newspapers
I media e la geometria solida Coni e Piramidi:
Youmath.it Library weschool.com Andreaminini.org Sapere virgilio.it Eduboom.it Geogebra.org Aula scienze scuola zanichelli.it Matematicamente.it Matematika.it Risolvi geometria.it Math.it Campus Hub scuola.it Youtube.com Skuola.net Matemania.it Pianeta bambini.it Matematica ok.com Davide Zizioli cloud Gobnf com formule
![]()
Cono e piramide retti Il cono video
Tronco di cono e di piramide Il tronco di cono video
Area della superficie di un tronco
Tabella riassuntiva dei coni e delle piramidi (1ª)
Tabella riassuntiva dei coni e delle piramidi (2ª)
Coni e piramidi Yahoo! Video YouTube
Cono: Volume, Superficie, Formule per Scuola Media Redooc
Ripassa le formule di geometria solida con un test Osmosi delle Idee sinapsi
Come calcolare la base di una Shape scienceaq
Che cos'è il cono retto capitello
![]()
![]()
GEOMETRIA SOLIDA - CONI E PIRAMIDI
DEFINIZIONI
Abbiamo già parlato del cono nel capitolo di introduzione alla geometria spaziale:qui ci occuperemo principalmente delle piramidi, cioè di quei coni aventi come direttrice un poligono.
Parleremo anche del cono circolare (fig. 301) perché il comportamento di questi due solidi è molto simile.
La differenza principale fra il cono circolare e la piramide è che il primo non è un poliedro, poiché in esso non si possono distinguere delle facce laterali.
In una piramide, invece, queste sono tante quanti sono i lati della base (fig. 302);
chiameremo poi spigoli laterali quelli comuni a due facce laterali adiacenti, spigoli di base quelli che delimitano quest'ultima.
Anche la piramide, come il prisma, può essere triangolare, quadrangolare, esagonale, ecc., a seconda che la base sia un triangolo, un quadrilatero, un esagono.
Si dice altezza della piramide la distanza che separa il vertice del piano della base.
Della piramide si può dare anche la seguente definizione più semplice:
La piramide è un poliedro limitato da un poligono e da tanti triangoli quanti sono i lati del poligono, aventi in comune un vertice esterno al poligono di base.
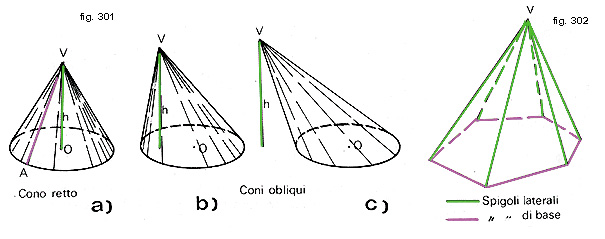
CONO E PIRAMIDE RETTI
Un cono circolare e una piramide si dicono retti quando il piede della perpendicolare condotta per il vertice coincide con il centro del cerchio di base.Per cerchio di base si intende, nel caso del cono, la base stessa(fig. 301):
al segmento VA si dà nome di apotema del cono.
Nel caso della piramide, invece, il cerchio di base è quello che eventualmente si può inscrivere nel poligono di base.
Ad esempio una piramide triangolare ha sempre un cerchio di base, poiché in un triangolo si può sempre inscrivere una circonferenza;
e quindi può essere retta, oppure no, mentre una piramide rettangolare non può in ogni caso essere retta, perché in un rettangolo non è possibile inscrivere una circonferenza.
Vediamo ora di renderci conto in maniera molto semplice della seguente regola.
La superficie laterale di una piramide retta è formata da triangoli aventi tutti la stessa altezza, che prende il nome di apotema della piramide.
Osserva la fig. 307:
il lato AB è perpendicolare al piano del triangolo VOH, quindi è perpendicolare anche al segmento VH, il quale risulta così l'altezza del triangolo ABV rispetto alla base AB.
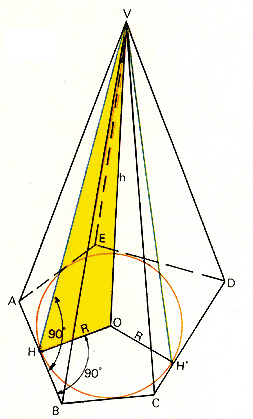
Lo stesso ragionamento si può ripetere per tutte le altre facce dove l'apotema rimane sempre lo stesso, se si osserva che:
L'apotema di una piramide retta è l'ipotenusa di un triangolo rettangolo avente per cateti l'altezza h e il raggio di base R.
Quindi possiamo già scrivere la formula che ci dà l'apotema:
basta applicare il teorema di Pitagora al triangolo VOH:
+-----
a = \¦h²+R² (1)
Concludiamo questo paragrafo ricordando che una piramide retta avente per base
un poligono regolare si dice a sua volta regolare.Le sue facce laterali sono tutte triangoli isosceli.
![]()
![]()
AREA DELLA SUPERFICIE
Ritagliando il cono circolare retto lungo una generatrice e lungo la circonferenza di base si ottiene l'area di un settore circolare di cui si conosce il raggio, che coincide con l'apotema del cono, e lo sviluppo di un arco, uguale alla circonferenza di base rettificata.Ricordando la (6) del capitolo sulle nozioni di geometria piana si ha:
A l = (2p r*a):2 = p ra (2)
L'area della superficie laterale di un cono circolare retto è uguale al prodotto delle lunghezze del raggio di base e dell'apotema moltiplicato per p .
Per ottenere l'area totale A, basterà aggiungere ad A, l'area della base p r2
A t=pra+pr2=pr(a+r)(3)
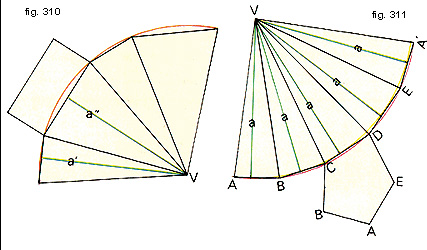
Lo sviluppo della piramide di fig. 307 è rappresentato in fig. 311.
Si nota che l'insieme delle facce laterali è equivalente a un unico triangolo avente altezza pari all'apotema e base uguale al perimetro della base della piramide.
Da qui la regola:
L'area della superficie laterale della piramide retta si ottiene moltiplicando il valore del semiperimetro per quello dell'apotema.
Indicando il perimetro di base con p si ha la formula:
A l = (p*a):2 (4)
Volendo l'area totale basta aggiungere l'area della base:
A(dep.t)=A(dep.l)+A(dep.B)=
p*a p*r p(a+r
= --- + --- = ------- (5)
2 2 2
Per la piramide regolare, tenendo conto che p = nl, dove n è il numero dei lati (6 nel caso di questa figura) ed l la loro lunghezza, in luogo delle (4) e (5) useremo le (6) e (7):
A l = (nl*a)/2 (6)
A t=A l+A B=
=(n*l*a)/2+(n*l*r)/2=
=nl(a+r)/2 (7)
Nel caso di una piramide non retta, infine, la superficie laterale va calcolata faccia per faccia.
(Osserva attentamente la fig. 310, dove è rappresentato lo sviluppo della piramide rettangolare:
nota che le facce laterali hanno altezze diverse).
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
VOLUME
Consideriamo un cono e un cilindro aventi la stessa altezza e per base la stessa linea chiusa qualsiasi vale la seguente regola:Il volume di un cilindro è il triplo di quello di un cono avente la stessa altezza e la stessa base.
V l=3 V 2 (8)
La regola ora enunciata può essere così espressa per i solidi che ci interessano:
Il volume di un cilindro circolare o di un prisma è il triplo di quello di un cono circolare o di una piramide avente la stessa altezza e base uguale o equivalente.
Di questo fatto ci si può rendere conto con un semplice esperimento.
Procuratevi un bicchiere a calice (cono) e una tazza cilindrica, ad esempio una tazzina da caffè, che abbia la stessa altezza del calice e lo stesso diametro.
Riempite d'acqua la tazzina utilizzando la misura del bicchiere:
ve ne occorreranno esattamente tre.
Passiamo dunque alle formule.
Ricordando come si calcola il volume del prisma, enunceremo la regola:
Il volume di un cono circolare (retto od obliquo) e quello di una piramide (retta od obliqua) si ottiene moltiplicando l'area della base per la misura dell'altezza e dividendo il risultato per 3.
V=(B*h)/3 (9)
In particolare per il cono circolare retto:
V=(p r2 h)/3 (10)
TRONCO DI CONO E DI PIRAMIDE
Intersechiamo un cono con un piano qualsiasi: delle due figure così ottenute quella che non contiene il vertice si chiama tronco di cono.Se il piano (a) è parallelo a quello che contiene la base (b), la sua intersezione con il cono è una figura piana simile alla base e la chiameremo base minore, mentre chiameremo l'altra base maggiore (v. fig. 318).
Questo solido viene chiamato tronco di cono a basi parallele o semplicemente tronco di cono. Lo stesso ragionamento si può ripetere per definire il tronco di piramide (fig. 319).
Qui però la figura da intersecare è un angoloide.
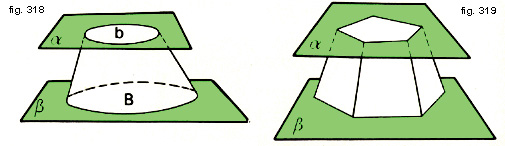
Un tronco di cono si dice circolare, retto od obliquo se ottenuto intersecando un cono circolare, retto od obliquo.
Così un tronco di piramide si dice regolare, retto o pentagonale, se ottenuto segando una piramide regolare o retta o pentagonale.
Anche il tronco di cono e il tronco di piramide retti hanno un apotema.
AREA DELLA SUPERFICIE DI UN TRONCO
In fig. 324 è rappresentato lo sviluppo della superficie di un tronco di cono circolare retto.La superficie laterale è un settore di corona circolare i cui archi sono le circonferenze delle due basi;
la larghezza coincide con l'apotema.
Ne deriva che:
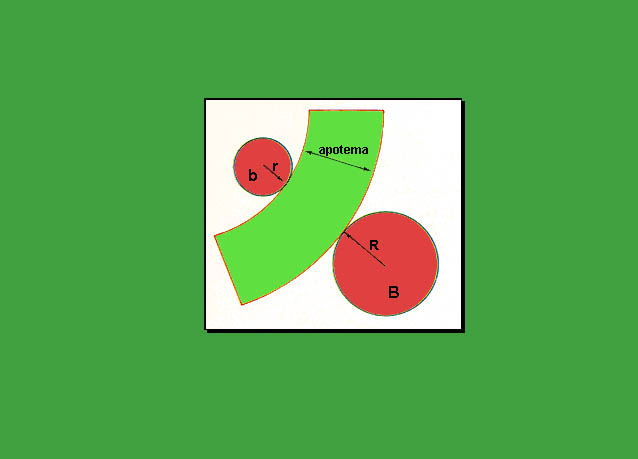
La superficie laterale di un tronco di cono circolare retto è equivalente a un trapezio avente per basi gli archi e per altezza l'apotema.
Da qui la formula:
(2p+2pR)*a
A(dep.l)=----------=pa(r+R)
2
(13)Volendo l'area totale basta aggiungere quella delle
due basi:A t= A l+b+BA t=
=pa(r+R)+pr2+pR2 (14)
La fig. 325 rappresenta lo sviluppo di un tronco di piramide retto:
la superficie laterale è costituita di tanti trapezi quanti sono i lati della base, aventi tutti la stessa altezza, coincidente con l' apotema.
Ne deriva che:
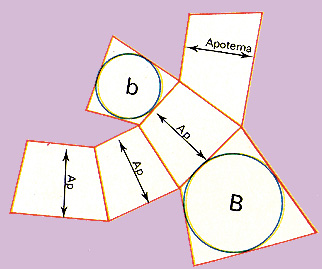
La superficie laterale di un tronco di piramide retta è equivalente a quella di un trapezio avente per base maggiore e minore rispettivamente i perimetri P e p delle basi del tronco e per altezza l'apotema.
A l=(p+P)a/2 (15)
Volendo l'area totale basta aggiungere quella delle due basi:
A t=a l+b+B (16)
VOLUME DI UN TRONCO
Enunciamo senza dimostrarla la seguente regola:Il volume di un tronco di cono o di piramide è la terza parte del prodotto dell'altezza per la somma delle aree delle basi aumentate della radice quadrata del prodotto delle aree delle basi stesse.
In particolare per il tronco di cono circolare si ha:
V=h[pr2+pR2+√(p2R2r2)]/3 (17)
E per il tronco di piramide:
+--
h(B+b+\¦Bb)
V = ----------- (18) 3
VERO O FALSO?
1) Una piramide è un cono avente per direttrice un poligono.2) Un tronco di piramide quadrata è un esaedro.
3) Un tronco di cono è retto se ha le basi parallele.
4) Una piramide che ha per base un poligono regolare e a sua volta regolare.
5) Gli spigoli laterali di una piramide appartengono a semirette generatrici.
1) Vero.
2) Vero.
3) Falso:
oltre ad avere le basi parallele, deve essere ottenuto dalla sezione di un cono retto.
4) Falso:
oltre ad avere per base un poligono regolare, il centro di questo deve coincidere con il piede del vertice.
5) Vero.
ESERCIZI
1) Una piramide retta ha l'area e il perimetro di base rispettivamente di m2 70 e di m 28.Sapendo che l'altezza misura m 3,75, calcolare l'area laterale.
Con la (3) inversa troviamo il raggio di base:
r=m[(2*70):28]=m 5
Ora ci serve l'apotema, calcolabile con la (1):
+---------
a = m \¦5²+ 3,75² =m 6,25
Infine applichiamo la (4):A l=m2[(6,25*28):2]=m2 87,5
2) Calcolare il perimetro di base di una piramide retta di volume m3 550, alta m 33 e il cui raggio di base misura m 20.
Troviamo subito il risultato applicando la prima delle (6) inverse:
p= m[(6*550):(20*33)]=m 5
3) Calcolare l'apotema di una piramide quadrata la cui superficie totale misura m2 720 e il lato di base m 12.
Ricordiamo che il raggio del cerchio inscritto in un quadrato è la metà del lato: nel nostro caso r = m 6.
Applichiamo la (10) inversa:
a=m[(2*720):(4*12)]-6=m 24
4) Calcolare il volume di una piramide ottagonale regolare alta cm 120 sapendo che il lato di base è di cm 50.
Il numero fisso b per l'ottagono è 2,414. Applichiamo la (9):
V= cm3[(502 *2,414*120):3]=
= cm3 241.400
5) Calcolare l'area laterale di una piramide rettangolare alta cm 12 sapendo che i lati della base misurano cm 18 e cm 32.
Calcoliamo a' e a'' con la (1):
+-----------
a'=cm \¦12²+(18:2)²= cm 15
+----------- a"=cm \¦12²+(32:2)²= cm 20
Ora applichiamo la (15):
A l=cm2(15*32)+(20*18)=
= cm2 840
6) Si deve costruire uno stadio calcistico. Le «curve» ospitano la maggior parte degli spettatori: queste hanno alla base un diametro di 100 metri e 140 alla sommità e sono alte circa 20 metri. Poiché le loro gradinate ospitano circa 4 spettatori ogni m2, si chiede quanti spettatori riusciranno a contenere.
Le due curve costituiscono insieme un tronco di cono circolare, di cui ci serve la superficie laterale; ma dobbiamo conoscere prima l'apotema:
+--------------
a=m \¦(70-50)²+ 20²=m 28,28
Ora possiamo calcolare l'area:A=m23,14*28,28*(50+70)=
= m2 10.665,9
Poiché ogni m2 contiene circa 4 spettatori, la capienza totale sarà di:
posti
4*10.665,9 = posti 42.623
7) Un ponte ferroviario poggia su piloni tronco-piramidali di pietra massiccia, a sezione quadrata; l'area della base minore è i 2/3 di quella della base maggiore, il cui lato misura m4,5 e l'altezza m 25. Si vuol sapere il peso di un pilone, il cui materiale ha un peso specifico di 3,2.
Dobbiamo trovare il volume e quindi ci servono le aree delle basi:
Base maggiore
A=m2 4,52=m2 20,25
base minore
A=m220,25*2/3=m2 13,5
Applichiamo ora la (18) del testo:

t(419,03*3,2)= t1340,9
![]()
Tabella riassuntiva dei coni e delle piramidi (1ª)
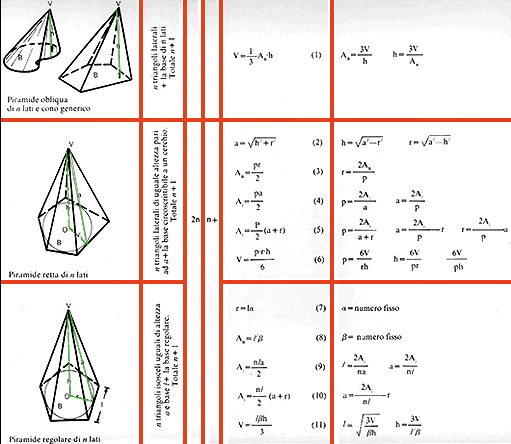
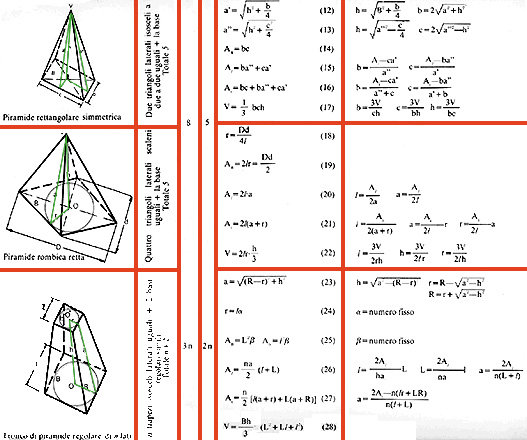
Tabella riassuntiva dei coni e delle piramidi (2ª)
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()
