Geometria Piana Superfici dei Poligoni.

Dizionari Enciclopedia Storia Link utili Down

Linea flashing backefro

GEOMETRIA PIANA - SUPERFICI DEI POLIGONI

SUPERFICI EQUIVALENTI

Due figure che coincidono perfettamente quando vengono sovrapposte si dicono uguali. Naturalmente, queste figure uguali occupano la stessa parte di piano, hanno cioè la stessa estensione. Si può quindi affermare che due figure uguali hanno uguale estensione.

Attenzione però: non sempre vale l'inverso di questa affermazione; può infatti capitare che due figure (o, più precisamente due superfici) abbiano uguale estensione senza essere uguali.

Fate a questo proposito un piccolo esperimento.

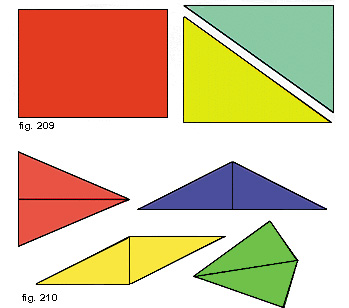
Ritagliate un rettangolo da un foglio di cartoncino; disegnate poi una diagonale e tagliate il rettangolo in due triangolini lungo questa diagonale (fig. 209).

E' facile ora comporre per mezzo dei due triangolini varie figure che non sono uguali al rettangolo di partenza perché non coincidono con esso quando proviamo a sovrapporli. Queste nuove figure però hanno la stessa estensione del rettangolo, perché sono state formate usando le stesse parti (fig. 210).

Fig. 209 e 210

Linea flashing backefro

Stabiliremo allora che:

Due superfici che hanno uguale estensione si dicono equivalenti.

Questo concetto di equivalenza può essere compreso facilmente pensando a un camper e a un monolocale: le due superfici abitabili hanno forma diversa ma estensione uguale.

L'equivalenza di superfici gode delle seguenti proprietà:

1) ogni superficie è equivalente a se stessa (riflessività);

2) se una superficie è equivalente a un'altra, questa seconda è equivalente alla prima (simmetria);

3) due superfici equivalenti a una terza sono equivalenti fra loro (transitività);

4) superfici uguali sono equivalenti;

5) somme di superfici uguali o equivalenti sono equivalenti;

6) differenze di superfici uguali o equivalenti sono equivalenti.

Esamineremo ora alcuni casi particolari di equivalenza di poligoni:

- Un parallelogrammo e un rettangolo aventi basi e altezze uguali sono equivalenti.

Infatti i trapezi HBCD e A'H'C'D' sono uguali e quindi hanno uguale estensione, e cosi anche i triangoli ADH e H'B'C'. Pertanto il parallelogrammo ABCD e il rettangolo A'B'C'D' sono equivalenti, come somme di figure uguali.

- Due parallelogrammi aventi uguale base e uguale altezza sono equivalenti.

Il parallelogrammo ABCD è infatti equivalente al rettangolo HECD; allo stesso modo, il parallelogrammo A'B'C'D' è equivalente al rettangolo E'H'C'D'. Si ha inoltre che HECD e E'H'C'D' sono uguali e quindi equivalenti. Risulta pertanto che sono equivalenti anche i due parallelogrammi ABCD e A'B'C'D'.

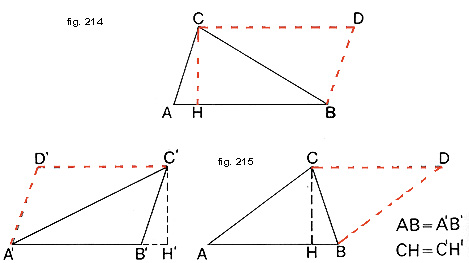
- Un triangolo è equivalente alla metà di un parallelogrammo avente uguale base e uguale altezza (fig. 214).

E' facile accorgersi di questo perché il lato CB del triangolo è nello stesso tempo la diagonale del parallelogrammo ABCD; ora, come già è stato detto, un parallelogrammo viene diviso da ciascuna diagonale in due triangoli uguali e quindi equivalenti.

- Due triangoli aventi uguale base e uguale altezza sono equivalenti (fig. 215).

Fig. 214 e 215

Per il caso precedente, ciascuno dei due triangoli è equivalente alla metà di un parallelogrammo avente uguale base ed uguale altezza. Ma risulta anche che i due parallelogrammi ABCD e A'B'C'D' sono equivalenti perché hanno base e altezza uguali. Saranno quindi equivalenti anche le loro rispettive metà, e cioè i triangoli ABC e A'B'C'.

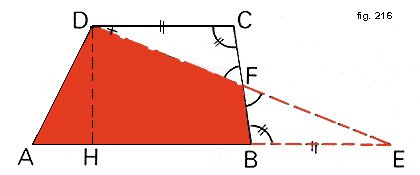
- Un trapezio è equivalente a un triangolo avente la stessa altezza e per base la somma delle sue basi (fig. 216).

Fig. 216

Il trapezio ABCD e il triangolo ADE hanno in comune il quadrilatero ABFD. Risulta inoltre, per il secondo criterio di uguaglianza dei triangoli, che DFC = BEF. Da questo segue che ABCD e ADE sono equivalenti perché somme di superfici uguali e quindi equivalenti.

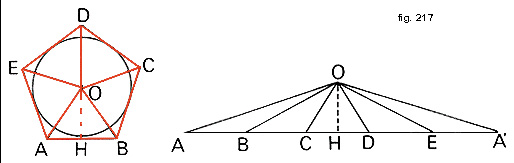
- Un poligono circoscritto a una circonferenza è equivalente a un triangolo avente per base la somma dei lati del poligono (perimetro) e per altezza il raggio della circonferenza (fig. 217).

Fig. 217

Poiché un poligono regolare può sempre essere circoscritto a una circonferenza, si può aggiungere che un poligono regolare è equivalente a un triangolo avente per base il perimetro e per altezza il raggio del cerchio inscritto.

Il poligono ABCDE circoscritto alla circonferenza di raggio OH e il triangolo AA'O sono infatti equivalenti perché entrambi sono somme di triangoli equivalenti (triangoli che hanno la stessa base e la stessa altezza).

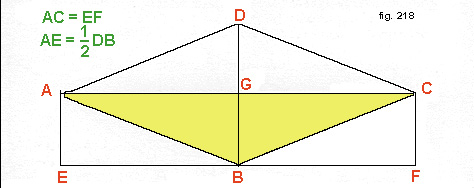
- Un rombo è equivalente a un rettangolo i cui lati sono una sua diagonale e la metà dell'altra (fig. 218).

Fig. 218

Il rombo ABCD e il rettangolo EFCA hanno in comune il triangolo ABC. Inoltre i triangolini AGD e DGC sono uguali ai triangolini AEB e CBF. ABCD e EFCA risultano quindi equivalenti essendo somme di superfici uguali.

Linea flashing backefro

AREA DEI POLIGONI

Una superficie può essere misurata confrontandola con un'altra superficie scelta come unità di misura, per vedere quante volte questa unità di misura è contenuta nella superficie data.

Ad esempio, se prendete un quadretto del vostro quaderno come unità di misura potete misurare la superficie di una pagina contando quante volte il quadretto è contenuto nella pagina cioè quanti quadretti ci sono su di essa.

La misura di una superficie è chiamata area.

Per quanto è stato detto nel paragrafo precedente, risulta che due superfici equivalenti hanno uguale area.

Fatte queste considerazioni, si può indicare il modo per misurare l'area dei più importanti poligoni.

AREA DEL RETTANGOLO

Disegnate sul vostro quaderno un rettangolo con la base lunga 10 quadretti e l'altezza 4 quadretti. Dividete la base in 10 parti uguali e tracciate le parallele all'altezza; lo stesso fate per l'altezza: dividetela in 4 parti uguali e tracciate le parallele alla base. In questo modo vi accorgerete che la superficie del rettangolo è stata divisa in un certo numero di quadretti tutti uguali, e che questo numero è uguale al prodotto del numero dei quadretti della base per il numero dei quadretti dell'altezza, cioè 10x4 = 40.

Questo significa che l'area del rettangolo è uguale al prodotto della misura della base perla misura dell'altezza.

Se indichiamo con A l'area e con b ed h rispettivamente le misure della base e dell'altezza, si ottiene quindi la formula:

A = b*h

AREA DEL QUADRATO

Poiché il quadrato ha tutti i lati uguali, si ha che l'area del quadrato è uguale al prodotto della misura della base per se stessa.

Indicando con l la misura del lato si ha la formula:

A = l*l= l²

AREA DEL PARALLELOGRAMMO

Nel paragrafo precedente avevamo stabilito che un parallelogrammo e un rettangolo aventi basi e altezze uguali sono equivalenti; sappiamo inoltre che due superfici equivalenti hanno uguale area. La formula dell'area del parallelogrammo sarà quindi la stessa dell'area del rettangolo:

A = b*h

AREA DEL TRIANGOLO

Abbiamo sopra dimostrato che un triangolo è equivalente alla metà di un parallelogrammo avente uguale base e uguale altezza. Di conseguenza, l'area del triangolo è uguale alla metà del prodotto della misura della base per la misura dell'altezza.

                              b*h
                          A = ---
                               2

AREA DEL TRAPEZIO

Dal momento che un trapezio è equivalente a un triangolo che ha la stessa altezza e per base la somma delle basi, l'area del trapezio è uguale alla metà del prodotto della somma delle misure delle due basi per la misura dell'altezza.

Se con b e b' indichiamo le due basi del trapezio, la formula dell'area sarà:

                             (b+b')*h
                        A = ---------
                                   2

AREA DEL POLIGONO CIRCOSCRITTO A UNA CIRCONFERENZA

Sappiamo che un poligono circoscritto a una circonferenza è equivalente a un triangolo avente per base la somma dei lati del poligono (il perimetro) e per altezza il raggio. Allora, se p è il perimetro del poligono e r il raggio della circonferenza inscritta, la formula dell'area sarà:

                                p*r
                          A = ---
                                 2

Linea flashing backefro

Guadagnare navigando.

Guadagnare navigando! Acquisti prodotti e servizi.

Guadagnare acquistando online.

Linea flashing backefro

AREA DEL POLIGONO REGOLARE

La superficie di un poligono regolare è equivalente alla superficie di tanti triangolini quanti sono i lati del poligono, aventi la base uguale al lato del poligono e l'altezza uguale al suo apotema. Pertanto l'area del poligono regolare è uguale alla metà del prodotto della misura del perimetro (somma dei lati) per la misura dell'apotema.

Se p indica il perimetro e a l'apotema, la formula dell'area del poligono regolare è:

                              p*a
                          A = ----
                               2

AREA DEL ROMBO

Sappiamo che la superficie del rombo è equivalente alla superficie di un rettangolo che ha come lati una diagonale del rombo e metà dell'altra. L'area del rombo è uguale al prodotto della misura di una diagonale per la metà dell'altra.

Indicando con d e d' le due diagonali si ha la formula:

                            d'   d*d'
                     A = d*--- = ----
                            2     2

Nella pratica sono moltissime le occasioni in cui bisogna saper calcolare l'area di una superficie. Ad esempio, prima di progettare una casa un geometra deve sapere quanto misura lo spazio a sua disposizione; allo stesso modo il contadino deve saper misurare l'estensione dei suoi campi.

IL TEOREMA DI PITAGORA

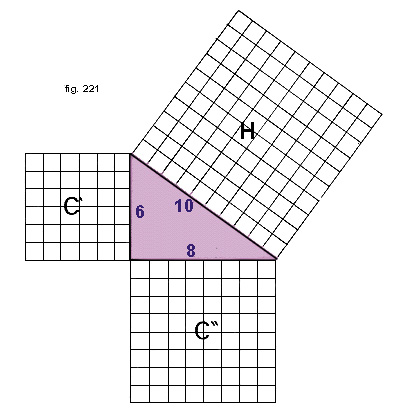
Il teorema di Pitagora costituisce un caso particolare della equivalenza di superfici. Esso afferma una proprietà dei triangoli rettangoli: trova perciò un vasto campo di applicazione in tutte quelle figure geometriche che hanno qualche triangolo rettangolo come componente. Questo importante teorema dice che:

In ogni triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti (fig. 221).

Fig. 221

Indicando con i la misura dell'ipotenusa e con c'e c'' le misure dei cateti si ha quindi:

i² = c'²+ c''²

Se provate a disegnare sul vostro quaderno un triangolo rettangolo con i cateti lunghi ad esempio uno 6 quadretti e l'altro 8 quadretti, l'ipotenusa avrà la lunghezza pari a 10 quadretti. Costruite poi sopra l'ipotenusa e sopra i cateti i rispettivi quadrati, che chiamiamo I,C',C''. Potete rendervi conto immediatamente che I contiene 10 * 10 = 100 quadratini, e che questo numero è uguale alla somma dei quadratini contenuti da C' e C''. Infatti: 6x6 = 36, 8x8 = 64, e 36+64 = 100.

Il teorema può però essere dimostrato in modo generale per mezzo delle considerazioni seguenti.

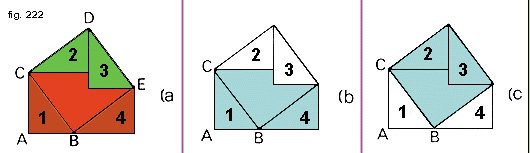
Disegnate (fig. 222) il triangolo rettangolo ABC; costruite il quadrato CBDE sull'ipotenusa e completate la figura come in a).

Fig. 222

E' facile accorgersi che i triangolini 1,2,3,4 sono uguali. La parte colorata in rosso sommata ai triangolini 1 e 4 è quindi equivalente alla stessa parte sommata ai triangolini 2 e 3 (rosso + marrone = rosso + verde).

Se fate attenzione vi accorgerete però che la parte colorata nella figura b) è equivalente alla somma dei quadrati costruiti sui cateti del triangolo ABC. Invece la parte colorata della figura c) rappresenta il quadrato costruito sull'ipotenusa CB. Questo vuol dire allora che il teorema di Pitagora è stato dimostrato, cioè che la somma dei quadrati costruiti sui cateti di un triangolo rettangolo è equivalente al quadrato costruito sull'ipotenusa dello stesso triangolo.

Il teorema di Pitagora, come si è detto, è molto importante per le sue molteplici applicazioni. Eccone alcune:

¦ trovare la misura dell'ipotenusa di un triangolo rettangolo, date le misure dei cateti.

La formula del teorema di Pitagora è: i²= c'²+ c''²; pertanto la misura dell'ipotenusa sarà la seguente:

                           +---------
                      i = \¦c'²+ c''²

¦ trovare la misura di un cateto di un triangolo rettangolo, date le misure dell'ipotenusa e dell'altro cateto.

Sempre partendo dalla formula del teorema di Pitagora è facile capire che: c'²= i²- c''²; e c''²= i²- c'². Pertanto la misura di ciascun cateto è data dalle formule:

              +---------                      +--------
         c'= \¦ i²- c''²                c''= \¦ i²- c'²

¦ trovare la misura della diagonale del quadrato di cui conosciamo il lato.

La diagonale di un quadrato lo divide in due triangoli rettangoli aventi come cateti i lati del quadrato e come ipotenusa la diagonale stessa. Se conosciamo il lato del quadrato possiamo allora applicare immediatamente il teorema di Pitagora per trovare la misura della diagonale:

               +------    +-----
          d = \¦ l²+l² = \¦ l²*2 = ¹l²*¹2 = l*¹2

¦ trovare la misura dell'altezza di un triangolo equilatero, data la misura del lato.

L'altezza di un triangolo equilatero lo divide in due triangoli rettangoli uguali, aventi per ipotenusa il lato del triangolo equilatero e per cateti l'altezza e metà del lato del triangolo equilatero. Ora se indichiamo con h l'altezza e con l il lato possiamo applicare il teorema di Pitagora nel seguente modo per trovare la misura dell'altezza:

                                     3
            h²= l²-(l/2)²= l²-l²/4 = - l²
                                     4

Estraendo la radice quadrata infine si ottiene:

                        +-----
                        ¦ 3     ¹3*l
                   h =  ¦ - l²= ----
                       \¦ 4       2

Il Teorema di Pitagora

VERO O FALSO?

1) Due figure sono uguali se hanno uguale estensione.

2) Due figure che hanno la stessa estensione hanno la stessa area e sono perciò equivalenti.

3) Un trapezio avente una base e l'altezza uguali a quelle di un rettangolo è ad esso equivalente.

4) Un triangolo rettangolo e un triangolo isoscele aventi rispettivamente un cateto e la base uguali e la stessa altezza sono equivalenti.
5) L'area del poligono regolare è uguale alla metà della somma dei lati del poligono moltiplicata per la distanza di ciascun lato dal centro del poligono stesso.

6) L'area del rombo è uguale alla misura della base per la misura dell'altezza.

7) In un triangolo rettangolo la misura dell'ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti.

Linea flashing backefro

1) Falso: due figure che hanno uguale estensione possono anche non essere uguali.

2) Vero.

3) Falso: un trapezio è equivalente a un triangolo avente la stessa altezza e per base la somma delle basi.

4) Vero.

5) Vero.

6) Falso: l'area del rombo è uguale alla metà del prodotto delle diagonali.

7) Falso: la misura dell'ipotenusa è uguale alla radice quadrata della somma delle aree dei quadrati costruiti sui cateti.

ESERCIZI

(Consultate la parte dedicata alle misure)

- Trasformate un triangolo scaleno in un triangolo rettangolo equivalente avente la stessa base.

- Trasformate un trapezio isoscele in un triangolo isoscele equivalente.

- Calcolate l'area di un rettangolo sapendo che il perimetro è di cm 136 e che la base è più lunga dell'altezza di cm 4 ( Riposta: cm²1152).

- L'area di un triangolo rettangolo misura cm²255 e un cateto è lungo cm 17.

Quanto misura l'altro cateto? (Risposta: cm 30).

- In un trapezio le basi e l' altezza misurano rispettivamente cm 33 cm 27 e cm 12.

Calcolate l'area (Risposta: cm²360).

- Determinate l' area del pentagono regolare avente il lato di cm 17 e il raggio del cerchio inscritto di cm 8. (Risposta: cm²340).

- Quanto misura l'ipotenusa di un triangolo rettangolo i cui cateti sono lunghi cm 5 e cm 12? (Risposta: cm 13).

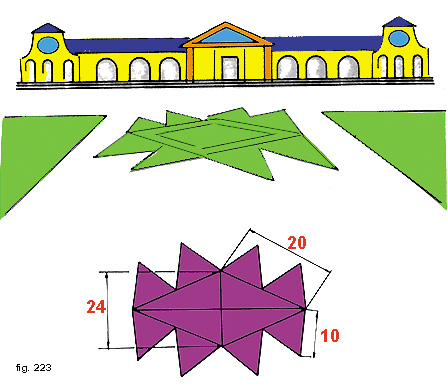
- Calcolate l'area dell'aiuola della fig. 223, sapendo che il lato della parte interna a forma di rombo è di m 20, che la diagonale minore della stessa parte misura m 24, e che gli otto triangolini uguali posti sui lati del rombo sono equilateri e hanno il lato uguale alla metà del lato del rombo (Nel calcolo delle radici quadrate, approssimate fino a due cifre dopo la virgola) (Risposta: m²730,4).

Fig. 223

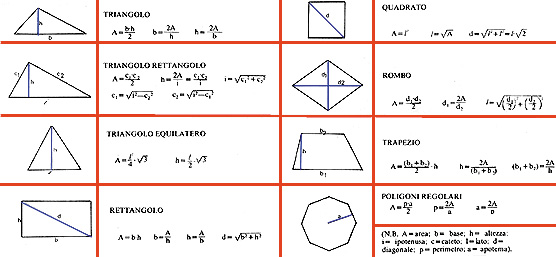
Tabella riassuntiva dei poligoni regolari