![]()
Somma degli angoli di un poligono
I quadrilateri
Il trapezio
I parallelogrammi
Poligoni inscritti, circoscritti e regolari
Vero o falso?
Esercizi
Geometria Piana e Solida Informatica Media Ecdl
Geometria piana e solida
Geometria Quadrilateri e Poligoni Gli Angoli Il Triangolo Linee sul Piano Geometria Piana Il Cerchio Superficie dei Poligoni Cilindri e Prismi Coni e Piramidi Gli Esaedri La Sfera Geometria Solida Nozioni Generali Solidi di Rotazione
Web link:
Yahoo! Video Geometria piana elementi fondamentali YouTube
La nascita della Geometria e i suoi "Elementi" Rai Cultura
![]()
![]()
GEOMETRIA PIANA - QUADRILATERI E POLIGONI
SOMMA DEGLI ANGOLI DI UN POLIGONO
Prima di passare dai poligoni con tre lati, i triangoli, ai poligoni con quattro lati, i quadrilateri, spiegheremo come calcolare la somma degli angoli interni e la somma degli angoli esterni di un poligono qualsiasi, cioè con un numero qualunque di lati.Si può dimostrare innanzitutto che:
- la somma degli angoli interni di un poligono è uguale a tanti angoli piatti quanti sono i lati meno due angoli piatti.
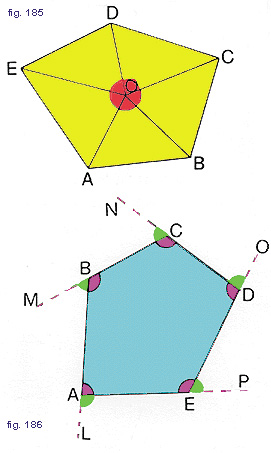
Come esempio disegnate un poligono a cinque lati (pentagono) ABCDE (fig. 185) e fissate un punto O al suo interno. Ora congiungete O con i cinque vertici A, B, C, D, E del poligono.
In questo modo si ottengono cinque triangolini: EOA, EOD, DOC, COB, BOA.
Dal capitolo precedente sappiamo che la somma degli angoli interni di un triangolo è uguale a un angolo piatto.
Per ottenere la somma degli angoli interni di ABCDE dovete allora moltiplicare un angolo piatto per il numero dei piccoli triangoli, cioè cinque.
Dal risultato di questa moltiplicazione bisogna sottrarre però un angolo giro cioè la somma degli angoli AôB, EôA, DôE, CôD, BôC, che appartengono ai cinque triangoli ma non al poligono.
Se n è allora il numero dei lati di un poligono qualsiasi, la somma degli angoli interni di questo poligono è data dalla formula:
(n-2)angoli piatti
Inoltre si può dimostrare che:
- la somma degli angoli esterni di un poligono è uguale a due angoli piatti.
Per angoli esterni si intendono gli angoli contenuti fra un lato e il prolungamento del lato successivo.
Nella figura 186 potete notare che ciascun angolo interno del poligono ha un angolo esterno come supplementare.
La somma degli angoli esterni sarà data allora dalla somma di tanti angoli piatti quanti sono i lati del poligono diminuita della somma degli angoli interni del poligono:
n angoli piatti-[(n-2)angoli piatti] = 2 angoli piatti
![]()
![]()
I QUADRILATERI
Come abbiamo accennato all'inizio del paragrafo precedente, i quadrilateri sono i poligoni con quattro lati.Due lati di un quadrilatero si dicono consecutivi se hanno un vertice in comune (ad esempio i lati AB e AD), opposti se non sono consecutivi (ad esempio i lati AB e DC).
Oltre ai lati, agli angoli e ai vertici, un quadrilatero ha due diagonali (nel disegno, CA e DB) che uniscono i vertici opposti.
La somma degli angoli interni di un quadrilatero è uguale a due angoli piatti:
(4-2) angoli piatti.
Ci sono due tipi particolari di quadrilateri:
il trapezio e il parallelogrammo.
IL TRAPEZIO
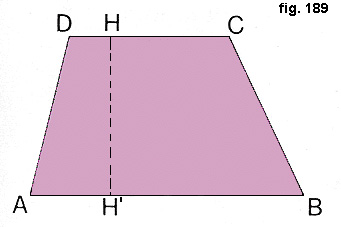
Il trapezio è un quadrilatero che ha due lati opposti paralleli.Nella fig. 189 il lato AB è parallelo al lato CD. AB è chiamato base maggiore, CD base minore.
DA e CB sono invece i lati, e la distanza HH' è l'altezza.
Nel capitolo precedente una illustrazione indicava come esempio di triangolo il deflettore della portiera di una automobile.
I finestrini di un'auto rappresentano invece degli esempi di trapezi.
Ci possono essere tre diversi tipi di trapezi:
a) il trapezio isoscele che ha i due lati uguali (DA = CB).
Questo tipo di trapezio si differenzia dagli altri per avere uguali le due diagonali (AC = BD) e gli angoli adiacenti a ciascuna delle basi (DAB = CBA; ADC = BCD).
Un esempio di trapezio isoscele è il cosiddetto «trapezio» usato dagli acrobati del circo per le loro fantastiche evoluzioni.
b) il trapezio rettangolo che ha uno dei lati perpendicolare alle due basi (DAB = ADC = angolo retto).
I «baffi» del musetto di una Formula 1 sono degli esempi di trapezi rettangoli.
c) il trapezio scaleno che ha i lati disuguali (AD è diverso da CB).
I PARALLELOGRAMMI
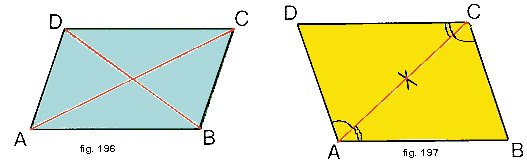
Il parallelogrammo è un quadrilatero con i lati opposti paralleliNel disegno di fig. 196 il lato AB è parallelo al lato DC e il lato CB parallelo al lato DA.
Ogni parallelogrammo è caratterizzato dal fatto che ciascuna diagonale lo divide in due triangoli uguali.
Si può verificare (fig. 197) che ACD = ACB e DBC = DBA.
Si tratta infatti di triangoli aventi un lato in comune e i due angoli adiacenti uguali (perché angoli alterni interni rispetto a due parallele tagliate da una trasversale).
Si può inoltre provare che i lati e gli angoli opposti sono uguali.
Fra tutti i parallelogrammi ve ne sono tre che godono di speciali proprietà;
essi sono:
il rettangolo, il rombo, il quadrato.
- Il rettangolo è un quadrilatero con quattro angoli retti.
Rispetto agli altri parallelogrammi ha la proprietà che le sue diagonali sono uguali.
Infatti i triangoli rettangoli ABC e ADB sono uguali, avendo DAB = CBA (entrambi retti), DA = CB perché lati opposti di un parallelogrammo, e il cateto AB in comune.
Si può allora concludere che le ipotenuse AC e DB sono uguali:
sono quindi uguali le diagonali del rettangolo.
- Il rombo è un quadrilatero con i quattro lati uguali (fig. 200).
Questa figura ha la speciale proprietà che le diagonali sono fra loro perpendicolari e bisettrici degli angoli.
Un oggetto che ci dà l'idea della figura geometrica del rombo è l'aquilone.
- Il quadrato è un quadrilatero con tutti i lati e gli angoli uguali (fig. 202).
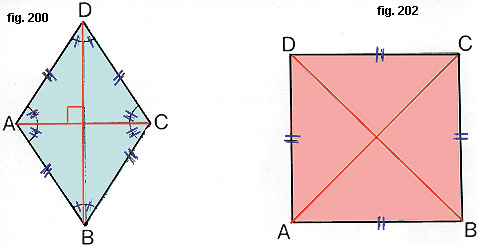
Il quadrato gode di tutte le proprietà generali del parallelogrammo, e, in più, di quelle particolari del rettangolo e del rombo;
infatti, le diagonali del quadrato sono uguali, perpendicolari fra loro e bisettrici degli angoli.
Anche il quadrato è una delle figure geometriche che più ci sono familiari:
basta pensare ai quadretti di un quaderno oppure al gioco degli scacchi o della dama.
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
POLIGONI INSCRITTI, CIRCOSCRITTI E REGOLARI
Se disegnate una circonferenza, fissate dei punti qualsiasi su di essa e poi tracciate la spezzata chiusa i cui vertici sono i punti stabiliti sulla circonferenza, otterrete un poligono inscritto.Un poligono si dice inscritto in una circonferenza quando tutti i suoi vertici sono punti appartenenti alla circonferenza.
Dalla fig. 204 potete rendervi conto che il centro della circonferenza è sempre equidistante dai vertici del poligono (OA = OB = OC = OD = OE = raggio), anche se può essere diversa la distanza del centro dai singoli lati (ad es. OH'OH).
Se invece disegnate delle rette (almeno tre) tangenti a una circonferenza prolungandole fino a incontrarsi, otterrete un poligono circoscritto (fig. 205).
Infatti, un poligono è circoscritto a una circonferenza quando i suoi lati sono tangenti alla circonferenza.
Attenzione! Non tutti i poligoni possono essere inscritti in una circonferenza o circoscritti ad essa.
Disegnate ora una circonferenza e dividetela in archi uguali (almeno tre).
Poiché ad archi uguali corrispondono corde aventi gli estremi in comune anch'esse uguali, il poligono risultante inscritto nella circonferenza avrà i lati uguali.
Nel disegno si ha cioè:
AB = BC = CD = DE = EF = FG = GH = HA, e inoltre:
AB = BC = CD = DE = EF = FG = GH = HA.
Essendo uguali anche i triangolini AOB, BOC, COD, DOE, EOF, FOG, GOH, HOA (avendo i tre lati uguali), saranno uguali anche gli angoli del poligono (essendo tutti somme di angoli uguali).
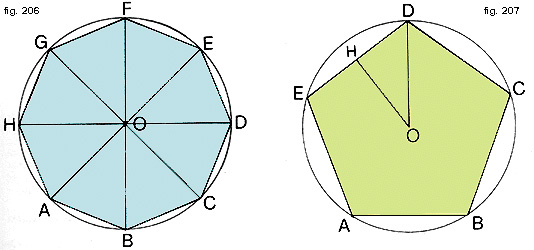
Procedendo nel modo indicato otterrete allora un poligono con tutti i lati e gli angoli uguali (fig. 206).
Un poligono di questo tipo si chiama poligono regolare.
Il centro della circonferenza in cui è inscritto un poligono regolare è equidistante non solo dai vertici ma anche dai lati del poligono; questo punto (O) si chiama centro del poligono (fig. 207).
Il raggio della circonferenza e quindi il segmento che unisce il centro con i vertici del poligono si chiama raggio del poligono (OD).
Si chiama invece apotema la distanza di ciascuno dei lati dal centro (OH).

Il quadrato è un caso di poligono regolare e si ottiene dividendo in 4 parti uguali la circonferenza.
Il pentagono regolare si ottiene invece dividendo la circonferenza in 5.
L'esagono regolare in 6 parti uguali, ecc.
Come esempi di poligoni regolari pensate ai bulloni usati per tutte le costruzioni metalliche.
VERO O FALSO?
l) La somma degli angoli esterni di un poligono è uguale a un angolo giro.2) La somma degli angoli interni di un poligono con otto lati è uguale a tre angoli giro.
3) Le diagonali di un quadrilatero sono uguali.
4) Le diagonali di un trapezio isoscele sono uguali.
5) Il parallelogrammo è un quadrilatero particolare con tutti gli angoli uguali.
6) Il rombo è un parallelogrammo con le diagonali perpendicolari fra loro.
7) Un poligono si dice inscritto quando è regolare e i suoi vertici appartengono a un cerchio.
8) Un poligono regolare può essere inscritto in una circonferenza e circoscritto ad una seconda circonferenza.
1) Vero.
2) Vero.
3) Falso: fra tutti i parallelogrammi è solo il rettangolo ad avere le diagonali uguali.
4) Vero.
5) Falso: il parallelogrammo è un quadrilatero con i lati opposti paralleli; solo il rettangolo e il quadrato hanno tutti gli angoli uguali.
6) Vero.
7) Falso: un poligono si dice inscritto quando tutti i suoi vertici sono su una circonferenza, e senza essere necessariamente regolare.
8) Vero.
ESERCIZI
(Per la risoluzione consultate la parte dedicata alle misure)- Un trapezio isoscele ha il perimetro di cm 150 e la base minore di cm 40.
Qual è la lunghezza degli altri lati, sapendo che la base maggiore supera di cm 10 il doppio del lato?
(Risposta: cm 60, cm 25)
- Il perimetro di un parallelogrammo è cm 120 e la differenza dei due lati consecutivi è cm 10.
Qual è la misura dei suoi lati?
(Risposta: cm 25, cm 35)
- Un trapezio isoscele ha gli angoli alla base maggiore di 60°.
Se il lato obliquo è lungo cm 34 e la base cm 55, quanto misura la base minore?
(Risposta: cm 21)
- Quanto è la somma degli angoli interni di un poligono con 12 lati?
- Inscrivete in una circonferenza di cm 4 di raggio un triangolo isoscele avente l'altezza uguale ai 5/8 del diametro.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()
