Dizionari Enciclopedia Storia Link utili Down

I media e il Cerchio:

Andreaminini.org Studysmarter.it Ilcalibro.it Matematicamente.it Risolvigeometria.it Mathcamp.it Youmath.it Math.it Superprof.it Library.weschool.com Matematicagratuitaperscuolesuperiori.it Skuola.net Maestraanita.it Learnex.it Orizzonteinsegnanti.it Esercizimatematica.com Risolvigeometria.it Dizionari.corriere.it Studenti.it Matematicafacile.it Teclaspelgatti.net Matematicaescuola.it Sapere.virgilio.it Matematika.it Sosmatematica.it Soloscuola.com Ilcalibro.it Brigantaggio.net Wordwall.net Fondazioneasfap.it Sostegno20.it Matemania.it Sapere.virgilio.it Campus.hubscuola.it Insights.gostudent.org Web.unica.it Impararefacile.com Iccivitella.it Ubimath.org Studiomatematica.it Studentville.it Valcon.it Scuolamania.it Php.math.unifi.it Theoremz.com Comesicalcola.it It.pinterest.com Webtutordimatematica.it Geometriapratica.it Scuolaelettrica.it Ripetizioni.it Mappe-scuola.com Scuolissima.com Pianetaproblemi.it Maestramarta.it Latteseditori.it Aiutodislessia.net Impariamoinsieme.com Youtube.com Risorsedidattiche.net Amicamat.it Valeriavecchi.it Conilfilodiarianna.it Maestramile.altervista.org Scienzeandmate.wordpress.com Aulascienze.scuola.zanichelli.it Pianetabambini.it Maecla.it Andreailmatematico.it Slideshare.net Mat.uniroma2.it Ilgomitolo.net Unife.it Members.supermat.it Itiscaramuel.it Lezionidimatematica.net It.openprof.com Matematicaoggi.it Geogebra.org Evaristogalois.it Edutecnica.it Matemania.it

Comunedicerchio.it Terremarsicane.it Ilcapoluogo.it Parma.repubblica.it Marsicalive.it Abruzzocitta.it News-town.it

Linea flashing backefro

Cerchio.

Superficie piana racchiusa da una curva:

luogo dei punti equidistanti da un punto interno detto centro. Tale curva si chiama circonferenza.

Il segmento che unisce il centro con un punto della circonferenza si chiama raggio;

quel segmento che unisce due punti della circonferenza passando per il centro si chiama diametro.

Il segmento che unisce due punti qualsiasi della circonferenza si chiama corda.

Nella prima metà del secolo scorso alcuni matematici si sono occupati dei sistemi di c. nel piano e nello spazio, le cui equazioni risultano combinazioni lineari di quelle di due o tre c. dati:

da questi studi derivano le affinità circolari di Möbius.

Sezioni del cerchio

Linea flashing backefro

L'anello di un canestro da basket è un esempio di circonferenza.

La circonferenza è una linea curva, chiusa (non ha un punto di inizio né di fine) e piana (la disegniamo su una superficie piana), i cui punti si trovano tutti alla stessa distanza dal centro.

Se mettiamo un anello su un foglio di carta e coloriamo la regione interna alla circonferenza, questa superficie piana colorata è un cerchio.

Gli elementi di una circonferenza

Gli elementi più importanti della circonferenza sono: raggio, corda, diametro e arco:

Il raggio è il segmento che unisce un qualunque punto della circonferenza con il centro.

Una corda è un segmento che unisce due punti della circonferenza.

La corda passante per il centro si chiama diametro.

Il diametro misura il doppio del raggio e divide la circonferenza in due semicirconferenze.

Un arco è la parte di circonferenza compresa tra due suoi punti.

Linea flashing backefro

La lunghezza di una circonferenza

La lunghezza di una circonferenza è uguale al suo diametro moltiplicato per il numero p (che vale 3,14 e si legge "pi greco"):

Lunghezza della circonferenza = diametro × p

Se volessimo sapere, ad esempio, quanto avanza la ruota di una bicicletta di 40 cm di diametro ogni volta che compie un giro, troveremmo la lunghezza della sua circonferenza:

Lunghezza = 40 × 3,14 = 125,6 cm

Se vuoi, puoi esercitarti con l'esempio seguente.

Se una giostra fa 30 giri, che distanza percorri se sali su un cavallino che si trova a 2 metri dal suo asse o centro?

In ogni giro, percorri una circonferenza di 2 m di raggio; pertanto, il diametro sarà:

diametro = 2 × raggio = 4 m

E la lunghezza della circonferenza:

lunghezza = diametro × 3,14

lunghezza = 4 × 3,14 = 12,56 m

Se fai 30 giri, la distanza percorsa sarà:

30 × 12,56 = 376,8 m

Posizioni di una retta e di una circonferenza

Su una superficie piana, una retta e una circonferenza possono trovarsi in una di queste tre posizioni:

1. La retta è esterna alla circonferenza: non hanno alcun punto in comune.

2. La retta è tangente alla circonferenza: hanno un punto in comune.

3. La retta è secante alla circonferenza: hanno due punti in comune.

Posizioni reciproche di due circonferenze

Due circonferenze su una superficie piana possono occupare diverse posizioni una rispetto all'altra, e possono essere: esterne, interne, concentriche, tangenti esterne, tangenti interne o secanti.

1. Esterne: non hanno alcun punto in comune.

2. Interne: non hanno alcun punto in comune.

3. Concentriche: hanno lo stesso centro, ma diversi raggi.

4. Tangenti esterne: hanno un punto in comune.

5. Tangenti interne: hanno un punto in comune.

6. Secanti: hanno due punti in comune.

Il cerchio

Il cerchio è la figura che formano una circonferenza e la sua area interna.

Non devi confondere la circonferenza, che è una linea curva, con il cerchio, che è la superficie delimitata dalla circonferenza.

Un settore circolare è la parte di cerchio compresa tra due raggi e l'arco da essi sotteso.

Un semicerchio è la superficie delimitata da un diametro e dalla semicirconferenza: è la metà del cerchio.

Un segmento circolare è la parte del cerchio compresa tra una corda e il suo arco.

L'Area del cerchio

L'area del cerchio di raggio R è uguale a p moltiplicata per il suo raggio al quadrato:

Area del cerchio = p × R^2

Proviamo a calcolare l'area dei cerchi dei due esempi seguenti.

1. Trova l'area di una pizza che misura 15 cm di raggio.

La pizza ha forma circolare, così che:

Area della pizza = p × R^2

Siccome R^2 = 15^2 = 225:

Area = 3,14 × 225 = 706,5 cm^2

2. Un bersaglio per frecce misura 40 cm di diametro.

Calcola l'area che occupa.

Siccome il diametro è il doppio del raggio:

Raggio = diametro : 2

Raggio = 40 : 2 = 20 cm

Siccome R^2 = 20^2 = 400:

Area = 3,14 × 400 = 1.256 cm^2

La corona circolare

Una corona circolare è la regione compresa tra due circonferenze di diverso raggio.

Per trovare l'area di una corona circolare, sottraiamo all'area del cerchio grande l'area del cerchio piccolo.

Se R è il raggio del cerchio grande e r quello del cerchio piccolo,

L'area sarà: p × R^2 - p × r^2

Se vuoi, puoi esercitarti con il seguente esempio:

Una torta rotonda è guarnita, nella parte centrale di 9 cm di raggio, con marmellata di fragole, e nella corona circolare che resta fino al bordo, di raggio 13 cm, con panna montata.

Trova la superficie di torta guarnita con panna montata.

Troviamo l'area di tutta la torta (del cerchio grande);

siccome R^2 = 13^2 = 169:

Area = p × R^2 = 3,14 × 169 = 530,66 cm^2

Ora troviamo l'area della parte centrale (del cerchio più piccolo);

siccome r^2 = 9^2 = 81:

Area = p × r^2 = 3,14 × 81 = 254,34 cm^2

L'area della torta guarnita con panna montata sarà:

Area della corona circolare = 530,66 - 254,34 = 276,32 cm^2

Cerchio.

s. m. (pl. cerchi m. ; cerchia f. )

1 Figura geometrica costituita da una porzione di piano racchiusa da una circonferenza - Circonferenza - Cerchio massimo, per una sfera, circonferenza avente lo stesso centro della sfera.

2 Attrezzo, struttura, figura a forma di cerchio - Cerchio della morte, acrobazia spettacolare di motociclisti o ciclisti che percorrono una pista circolare elevata verticalmente.

3 Ciò che ha forma circolare e cinge qualcosa: cerchio della botte.

4 Gruppo di cose o persone disposte in circolo - Fare cerchio attorno a qualcuno., circondarlo.

Settori circolari

Cerchio e sfera.

Il cerchio è una figura a due dimensioni definita come il luogo dei punti del piano equidistanti da un punto fisso detto centro.

La figura analoga in tre dimensioni è la sfera, anch'essa definita come il luogo dei punti (dello spazio, questa volta) equidistanti dal centro.

In figura sono riportate le formule per determinare la lunghezza di un arco di circonferenza, l'area di un settore circolare, l'area della calotta sferica e il volume di un settore sferico.

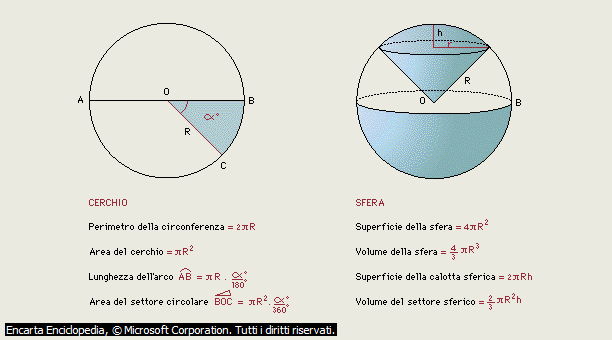
Cerchio e Sfera - Calcoli su,

Microsoft ® Encarta ® 2008.

Cerchio.

Superficie piana racchiusa da una curva:

luogo dei punti equidistanti da un punto interno detto centro.

Tale curva si chiama circonferenza.

Il segmento che unisce il centro con un punto della circonferenza si chiama raggio;

quel segmento che unisce due punti della circonferenza passando per il centro si chiama diametro.

Il segmento che unisce due punti qualsiasi della circonferenza si chiama corda.

Nella prima metà del secolo scorso alcuni matematici si sono occupati dei sistemi di c. nel piano e nello spazio, le cui equazioni risultano combinazioni lineari di quelle di due o tre c. dati:

da questi studi derivano le affinità circolari di Möbius.

Cerchio

Linea flashing backefro

Guadagnare navigando.

Guadagnare navigando! Acquisti prodotti e servizi.

Guadagnare acquistando online.

Linea flashing backefro

Lunghezza della circonferenza

Circonferenze rettificate

Lunghezza di un arco

La lunghezza di una arco è proporzionale all'ampiezza dell'angolo che lo sottende

Arco sotteso da un angolo di 360° corrisponde alla circonferenza

Area del cerchio Grafico

Area di un settore circolare Somma area settori circolari di altezza uguale al raggio Scomposizione area del settore

Area di una corona circolare (Area della corona circolare) Corona circolare equivalente a un trapezio

Vero o falso?

E sercizi Calcolo del raggio della Luna Calcolo del raggio interno della corona circolare

Tabella riassuntiva del cerchio

Vocabolario

Ripasso di matematica Geometria del piano euclideo Circonferenza e cerchio

Aritmetica Geometria Informatica

Geometria Piana e Solida

Elementi Fondamentali della Geometria Gli Angoli Il Triangolo Linee sul Piano Quadrilateri e Poligoni Superficie dei Poligoni Cilindri e Prismi Coni e Piramidi Gli Esaedri La Sfera Geometria Solida Nozioni Generali Solidi di Rotazione

Geometria piana il cerchio Yahoo!

Geometria piana il cerchio YouTube

Rai Scuola Geometria piana il cerchio

Amica Matematica Il Cerchio

GEOMETRIA PIANA - IL CERCHIO

LUNGHEZZA DELLA CIRCONFERENZA

Se avvolgiamo con un metro da sarto una ruota e leggiamo il valore corrispondente, avremo una misura della sua circonferenza.

Analogamente, controllando con una riga la lunghezza della traccia di tintura lasciata da un pennello a rullo in un giro completo avremo una misura del suo contorno.

Le lunghezze AB e A'B' si chiamano circonferenze rettificate.

Possiamo subito verificare che:

    A B    A'B'
    --- = ----- = 3,14
     D      D'

Il numero 3,14 viene indicato con il simbolo p (leggi «pi greca»).

Compiendo molte altre esperienze come questa arriveremo a dedurre la seguente proprietà:

il rapporto tra la lunghezza c di una circonferenza e il suo diametro d è sempre uguale al numero p:

c = p d d = c/p (1)*

Possiamo quindi trarre la seguente regola:

La lunghezza di una circonferenza si ottiene moltiplicando il valore del raggio r per 2p:

c = 2p r (2)

Si tenga comunque presente che il rapporto fra la lunghezza di una circonferenza e il suo diametro non è mai un numero esatto:

il valore 3,14 è approssimato, si può cioè ottenere un valore diverso ricorrendo a una misura più accurata, ad esempio 3,1415, oppure 3,141592, ecc.

Infatti le cifre decimali di p si succedono infinite e senza alcuna regola, a differenza di quanto avviene nei decimali periodici.

Anche per questo motivo p si chiama numero trascendente.

LUNGHEZZA DI UN ARCO

Dividiamo una circonferenza in due parti uguali AB e BA (semicirconferenze);

dividiamo quindi la semicirconferenza BA in due parti uguali (quadranti) BC e CA;

dividiamo infine un quadrante in due parti uguali, CD e DA.

Misurando gli angoli sottesi dagli archi, è facile constatare che AOB = 180°, BOC = 90°, COD = 45°.

Dimezzando quindi un arco si dimezza anche l'angolo al centro che lo sottende.

Possiamo dedurre quindi la seguente proprietà:

La lunghezza di una arco è proporzionale all'ampiezza dell'angolo che lo sottende.

Infatti:

La lunghezza di una arco è proporzionale all'ampiezza dell'angolo che lo sottende

Consideriamo l'archetto HH' sotteso da un angolo di 1°.

La sua lunghezza corrisponde alla 360esima parte di una circonferenza,

essendo questa sottesa da un angolo di 360°, e può essere preso come unità di misura;

infatti HH'/1° = c/360°.

Angoli al centro della circonferenza

Se n° è l'ampiezza dell'arco, si ha:

Linea flashing backefro

Guadagnare navigando.

Guadagnare navigando! Acquisti prodotti e servizi.

Guadagnare acquistando online.

Linea flashing backefro

Arco sotteso da un angolo di 360° corrisponde alla circonferenza

* I numeri accanto alle formule corrispondono a quelli della Tavola riassuntiva del cerchio, posta alla fine del capitolo.

Area del cerchio

Per calcolare l'area del cerchio, possiamo fare una prima approssimazione considerando quella di un poligono regolare inscritto nella sua circonferenza.

Maggiore è il numero dei lati del poligono, migliore sarà l'approssimazione.

Questo metodo era utilizzato dagli antichi greci quando ancora non si conosceva il numero p.

Oggi, quale metodo di approssimazione possiamo utilizzare?

1. Calcoliamo l'area di un cerchio

1.1. Per approssimazione

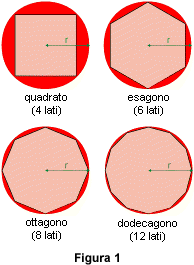
È possibile dimostrare che i poligoni rappresentati in figura 1 hanno le aree date dalle seguenti formule:

Il quadrato ha un'area uguale a 2xr^2 ;

L'esagono ha un'area uguale a circa 2,6xr^2 ;

L'ottagono ha un'area uguale a circa 2,8xr^2 ;

Il dodecagono ha un'area uguale a 3xr^2.

Figure geometriche circoscritte

1.2. Con la formula esatta

L'area di un cerchio di raggio r è uguale a p x r^2. Si ricordi che p vale circa 3,14.

Quindi: Area del cerchio = p x r^2 = p x r x r.

Per applicare questa formula, A ed r devono essere espressi in unità di misura corrispondenti;

ad esempio, se r è in Cm, A sarà espresso in CMQ.

2. Esempi

2.1. Primo esempio

Vogliamo calcolare l'area Area di un cerchio di raggio 10 Cm.

p x 10 x 10 = 100 p 314 quindi A = 314 CMQ.

2.2. Secondo esempio

Vogliamo calcolare l'area Area di un cerchio di 25 M di diametro.

Il raggio è uguale a 12,5 M (ovvero, la metà di 25 M.).

p x 12,5 x 12,5 = 156,25 p = 490,625 quindi A = 490,625 MQ.

Ripasso di matematica

AREA DEL CERCHIO

Osserviamo in fig. 228 che l'area del settore circolare OAA' è sempre maggiore di quella del triangolo OAA'.

Fig. 228

Tuttavia la differenza fra queste due aree (a colori nella figura) diviene insignificante quando il settore è molto piccolo.

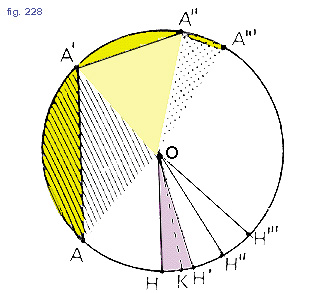
Area del cerchio

Se consideriamo infatti il settore OHH', ci accorgiamo che la sua area è praticamente uguale a quella del triangolo OHH':

la base di questo triangolo è a sua volta molto prossima all'arco HH' e la sua altezza OK è praticamente uguale al raggio r.

La sua area è quindi:


   HH'*r
   -----
     2

Ora, se immaginiamo il cerchio composto da tanti piccoli settori OHH', OH'H", OH"H"', ecc., la sua area sarà data dalla somma delle aree dei settori che hanno tutti altezza uguale al raggio e le cui basi sommate danno in totale la circonferenza.

Somma area settori circolari di altezza uguale al raggio

Riassumiamo quanto esposto nella seguente regola:

L'area del cerchio equivale a quella di un poligono regolare avente come perimetro la circonferenza e come apotema il raggio.

Essa si ottiene moltiplicando per q il quadrato del raggio.

AREA DI UN SETTORE CIRCOLARE

Consideriamo il cerchio come somma di 360 settori circolari di ampiezza 1°.

L'area di questo settore equivale perciò alla 360esima parte dell'area del cerchio, e può essere assunta come unità di misura.

Da qui la regola:

L'area di un settore circolare di ampiezza n° è pari a n volte quella del settore di ampiezza 1°:

 		  pr²
A sett.= n*-----  (5)
            360

Scomponiamo ora l'area del settore nel seguente modo:

Scomposizione area del settore

Il primo fattore è esattamente la lunghezza l dell'arco.

Ne deriva la seguente osservazione:

L'area di un settore circolare equivale a quella di un triangolo di base l e altezza r.

AREA DI UNA CORONA CIRCOLARE

Si nota facilmente che l'area della corona circolare è la differenza fra le aree del cerchio maggiore e di quello minore.

Area della corona circolare

E' comunque utile osservare che la corona circolare è equivalente a un trapezio avente per basi le circonferenze rettificate e per altezza la larghezza l della corona:

            2pR+2pr
  A corona= ------- * l  (8)
               2

VERO O FALSO?

1) Si dice circonferenza rettificata il perimetro di un cerchio.

2) Il numero p è il rapporto fra la misura della circonferenza e il suo raggio.

3) Il cerchio è equivalente a un triangolo di base uguale alla sua circonferenza e di altezza uguale al diametro.

4) L'area di una corona circolare è sempre minore di quella del cerchio esterno e maggiore di quella del cerchio interno.

5) L'area di un settore circolare è proporzionale alla sua ampiezza.

1) Vero.

2) Falso: è il rapporto fra la misura della circonferenza e il suo diametro.

3) Falso: l'altezza è pari al raggio.

4) Falso: può essere minore anche dell'area del cerchio interno, quando la larghezza è abbastanza piccola.

5) Vero.

ESERCIZI

(I numeri accanto alle formule corrispondono a quelli della Tavola riassuntiva sul cerchio)

1) Calcolare la circonferenza di una ruota di locomotiva del diametro di m 2,1.

Applicando la formula (2) avremo:

C=m*(3,14*2,1)=

=m 6,59

2) Il nome del grande matematico Archimede è stato dato a uno dei maggiori crateri circolari della Luna.

La sua superficie si estende per circa 9600 km².

Calcolare il suo raggio. Applicando la formula (3) inversa si ha:

Calcolo del raggio della Luna

3) Un settore circolare dell'ampiezza di 30° ha il raggio di cm 16.

Calcolarne l'area.

Calcoliamo dapprima l'area del cerchio, con la (3):

Acer.=

=cm²(3,14*16²)=

=cm²803,84

Ora possiamo applicare la (6):

Asett.=

=cm²(803,84*30:360)=

=cm²66,99

4) Calcolare la lunghezza dell'arco di un settore circolare la cui area misura m² 78,5 e il raggio cm 15.

Applicando la (7) inversa si ha:

l=m(2*78,5:15)=

=m 10,47

5) Calcolare l'ampiezza di un arco di circonferenza lungo m 3,4 e di raggio 4 m. Calcoliamo prima la circonferenza con la (1):

c = m(2*3,14*4)=

=m 25,12

Ora possiamo applicare la prima delle (5) inverse:

n°=(360°*3,4:25,12)=

= 48° (risultato approssimato)

6) Calcolare il raggio interno di una corona circolare di area m² 401,92, il cui raggio esterno misura m 18.

Applichiamo la seconda delle (10) inverse:

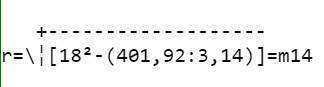
Calcolo del raggio interno della corona circolare

Proviamo ora ad affrontare un problema più complesso.

La pavimentazione speciale per la pista di uno stadio olimpico viene a costare circa 11 euro al m².

Sapendo che i rettilinei sono lunghi m 100, che il raggio interno della pista è di m 31,85 e la larghezza della pista di m 6, proviamo a calcolare il costo complessivo.

Naturalmente ci serve subito l'area, composta dei due rettangoli C e D e delle parti A e B che insieme formano una corona circolare; poi la moltiplicheremo per il prezzo di un m² e avremo il costo totale.

- Calcoliamo il raggio esterno R che è uguale a (r+l):

m (31,85+6)=

=37,85 m

- Calcoliamo l'area della corona:

m²3,14(37,85²- 31,85²)=

=1313,15m²

- Aggiungiamo l'area dei due rettangoli:

m²1313,15+2(6¦100)=

=2513,15 m²

- Moltiplichiamo l'area totale per il prezzo di un m² :

Euro11*2513,15=

=Euro 27.644,65

Il costo totale risulta di Euro 27.644,65.

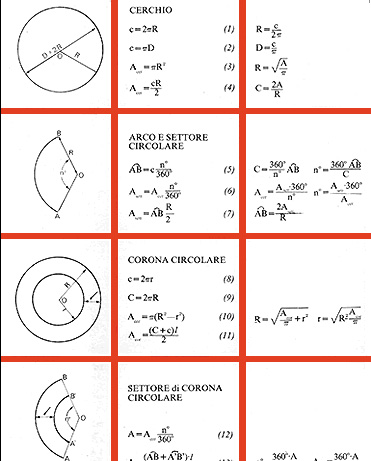
Tabella riassuntiva del cerchio

Vocabolario I F GB D

accerchiare.

(v. tr.), chiudere in un cerchio, circondare.

Inglese

to encircle

Francese

entourer

Tedesco

einkreisen

anèllo.

1 (s.m.), oggetto circolare, cerchio. 2 oggetto ornamentale che si porta al dito. 3 metamero: segmento del corpo degli anellidi. 4 strato ligneo che si forma in un anno sul tronco delle piante legnose. 5 chim. aggruppamento atomico. 6 sport. una forma di pista. 7 (pl. f.), poet. riccioli.

Inglese

(m.) muscle orbi culaire

Tedesco

(m.) Ringmuskel

quadrante.

(s.m.), 1 ciascuna delle quattro regioni in cui un piano è diviso da assi cartesiani; ciascuna delle quattro parti in cui un cerchio viene diviso da diametri ortogonali: - della bussola, ciascuno dei quattro settori compresi tra due punti cardinali contigui. 2 scala graduata di uno strumento di misura: - dell'orologio. 3 strumento astronomico usato per misurare la distanza angolare.

Inglese

quadrant

Francese

(m.) cadran

Tedesco

(m.) Quadrant

quadratura.

(s.f.), 1 atto, effetto del quadrare; porzione di superficie divisa in quadrati: la - del foglio; - mentale, (fig.), chiarezza di idee. 2 in geom. riduzione di una figura geometrica in un quadrato equivalente: - del cerchio, operazione insolubile mediante i metodi della geometria elementare, tale espressione viene usata anche in senso figurato per indicare una cosa assurda, impossibile. 3 in mat. operazione di elevazione al quadrato. 4 in astronomia differenza di longitudine di 90° fra due astri. 5 in arte pittura murale prospettica. 6 in contabilità operazione del quadrare.

Inglese

squaring

Francese

(f.) quadrature

Tedesco

(f.) Abvierung

radiale.

(agg.; mat. fis.), che è nella direzione del raggio di un cerchio: linea -.

Inglese

radial

Francese

radial

Tedesco

radial

raggio.

(s.m.), 1 ciascuna delle linee lungo le quali la luce sembra propagarsi da un corpo luminoso. 2 fig. attimo di illuminazione spirituale. 3 in fis. qualsiasi radiazione elettromagnetica o corpuscolare. 4 in geom. ciascuno dei segmenti che vanno dal centro alla circonferenza di un cerchio. 5 parte delle ruote che unisce il mozzo al cerchione.

Inglese

ray

Francese

(s.m.), parte del compasso usata per tracciare un cerchio.

Inglese

exchangeable point

Tedesco

(m.) Einsatz

tamburello.

(s.m.), 1 strumento musicale costituito da una membrana tesa su un cerchio di legno. 2 arnese simile al precedente, usato come racchetta nel gioco omonimo. 3 telaio per ricamare.

Inglese

tambourine

Francese

(m.) tambourin

Tedesco

(n.) Tamburin

tondo.

(agg.), 1 di forma rotonda; cifra tonda, senza frazioni di unità; parlare chiaro e tondo, esplicitamente; carattere -, preciso. 2 (fig.), grossolano, semplicione. 3 (s.m.), circolo; giro: in -, a -, tutto intorno, in cerchio. 4 dipinto elemento decorativo di forma circolare. 3 oggetto in genere di forma circolare, piatto, vassoio. 6 pezzi di legno usato per i camini.

Inglese

round

Francese

rond

Tedesco

rund

circŭlus

i, m.: circolo, cerchio, orbita dei pianeti; adunanza, società.

circus

i, m.: circo (edificio di figura ellittica destinato alle corse di cavalli e di cocchi); cerchio, circolo, circonferenza, orbita. Esempio: Circus Maximus, Circo Massimo.

collĭgo

is,collēgi, collectum, colligĕre (cum, lego), TR. 3ª: raccogliere, radunare, ammassare; restringere; conseguire, acquistare, acquistarsi, guadagnarsi; conchiudere; trattenere, reprimere; riepilogare, meditare, contare, calcolare, sommare; se colligere, riunirsi; ripigliar animo, riaversi, tornare in sé coprirsi; chiudersi. Esempi: sarmenta virgultaque colligere, raccogliere fascine di frasche e di arbusti; ex agris ingentem numerum hominum colligere, dalle campagne raccogliere un grande numero di uomini; benevolentiam civium colligere, guadagnarsi la benevolenza dei cittadini; colligere facete dicta, raccogliere detti spiritosi; omnia bella civilia colligere, ricapitolare gli avvenimenti di tutte le guerre civili; collidere pulverem Olympicum, coprirsi di polvere olimpica (gareggiare nei giuochi olimpici); luna cum colligit ignes, quando la luna raccoglie la sue corna (ossia quando la luna si fa piena); collidere spiritum, ripigliar fiato; colligere animum (o collidere se), ripigliar animo; collidere iram, adirarsi; colligere sitim, aver sete; colligere invidiam crudelitate (o collidere invidiam crudelitatis), incorrere nell'odio altrui per la propria crudeltà; colligere se in arma, coprirsi con lo scudo; colligere orbem, restringere il cerchio; colligere se in umbras, chiudersi in una vita oscura; castra movere et vasa colligere, levare il campo e fare i bagagli; se ex maximo timore colligere, riaversi da una grande paura, animo veteres calamitates colligere, meditare le antiche sventure; in spiram se collĭgit anguis, il serpente si raccoglie nelle sue spire; inde collĭgit paucitatem hostium, da ciò deduce la scarsezza dei nemici.

complector

complectĕris, complexus sum, complecti, TR. 3ª dep.: abbracciare, contenere, cingere, comprendere, circondare; favorire; accogliere; associare; concludere. Esempi: complecti aliquem, abbracciare uno; collem opere complecti, cingere un colle con fortificazioni; orbis qui reliquos omnes complectitur, il cerchio che contiene tutti gli altri; complecti amplissimos viros ad scelus, associare al proprio delitto i più illustri personaggi; complecti inter se, abbracciarsi; complecti aliquem omnibus studiis, favorire uno con ogni impegno; dextram completus euntis, prendendo la destra di lui che andava; complecti philosophiam, coltivare la filosofia; quod cogitatione tantum et mente complectimur, ciò che solo col pensiero e colla mente comprendiamo; una comprehensione omnia complecti, raccogliere tutto in un pensiero; effigiem auro complecti, legare in oro un ritratto; somnus me complectitur, mi prende il sonno; aliquem beneficio complecti, render un beneficio a qualcuno; complecti aliquid animo, arrivare a comprendere una cosa col pensiero; centum complexa nepotes, stringendosi al seno i suoi innumerevoli discendenti.