![]()
Confronto e operazioni fra angoli
Rette perpendicolari e rette parallele
GEOMETRIA PIANA - GLI ANGOLI
DEFINIZIONE E CLASSIFICAZIONE
Fissate un punto qualsiasi sul piano, ad esempio O, e tracciate a partire da questo punto la semiretta OA.Il punto O sarà allora l'origine della semiretta OA.
![]()
![]()
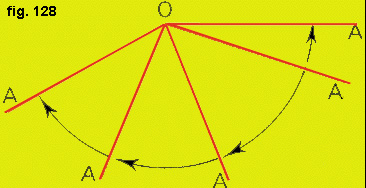
Ebbene, se ora fate ruotare la semiretta OA intorno all'origine prefissata 0, potrete ottenere diverse figure, ciascuna delle quali è formata dalla posizione iniziale della semiretta OA e dalla posizione assunta dalla stessa semiretta dopo che è stata fatta ruotare sul piano intorno all'origine in uno fra tutti i modi possibili.
Queste diverse figure si chiameranno angoli (figura 128).
Come esempio concreto potete pensare alle lancette di un orologio:
tenete ferma la lancetta delle ore e fate ruotare quella dei minuti in tutti i modi che volete.
Le lancette dell'orologio in questo modo formeranno degli esempi concreti di angoli;
e più precisamente, il centro dell'orologio rappresenterà il vertice dei vari angoli, mentre le lancette saranno i lati degli stessi.
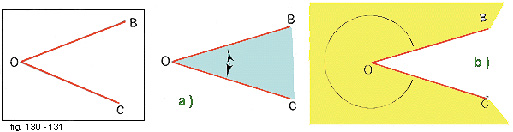
Un angolo si indica con tre lettere maiuscole:
una al vertice e una su ciascuno dei due lati (fig. 130).
Lo stesso angolo può inoltre essere indicato scrivendo la dicitura BôC.
Attenzione però!
BôC e il suo disegno in realtà non rappresentano un unico angolo, bensì i due angoli di figura 131.
![]()
![]()
Nel disegnare la figura bisogna sempre avere l'accortezza di specificare nel modo indicato a quale dei due angoli ci si riferisce.
Allo stesso modo, dovremo riferirci alla fig. 131
a) come all'angolo convesso BôC, e alla 131
b) invece come all'angolo concavo BôC.
Il modo per distinguere gli angoli convessi da quelli concavi consiste semplicemente in questo:
- gli angoli convessi sono quelli che non contengono il prolungamento dei lati;
- gli angoli concavi invece sono quelli che contengono il prolungamento dei lati.
Stabiliamo comunque di specificare, d'ora in poi, solo se ci si riferisce all'angolo concavo.
In un angolo AôB, si parlerà perciò di «angolo AôB» (sottintendendo «convesso») e di «angolo concavo AôB».
La vela della barca forma un angolo convesso, mentre lo sfondo che circonda la vela stessa forma un angolo concavo.
Esamineremo ora alcuni angoli particolari.
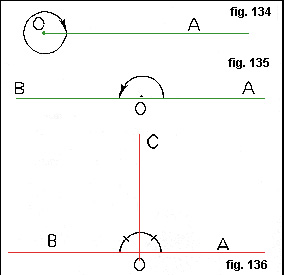
Se riprendete la semiretta OA facendola ruotare intorno all'origine O in modo tale che essa torni nella posizione di partenza, l'angolo generato da questo movimento è detto angolo giro (fig. 134.
Se invece fate ruotare OA in modo tale che essa vada a situarsi sul prolungamento opposto OB della stessa semiretta OA, l'angolo generato in tal modo si chiamerà angolo piatto (fig. 135).
Disegnate ora un angolo piatto AôB su un foglio di carta e ripiegatelo in modo tale che la semiretta OA si sovrapponga alla semiretta OB (in modo tale cioè che i lati OA e OB coincidano).
In questo modo l'angolo piatto viene diviso in due parti che sono uguali perché si sovrappongono perfettamente.
Tracciate allora una nuova semiretta OC lungo la ripiegatura:
otterrete i due angoli AôC e BôC, ciascuno dei quali è uguale alla metà dell'angolo piatto AôB ed è chiamato angolo retto (fig. 137).
Un esempio molto familiare di angolo retto è l'angolo di un campo di calcio, il cosiddetto corner.
Come è stato detto, la semiretta OC divide l'angolo piatto BôA in due angoli retti uguali BôC e AôC.
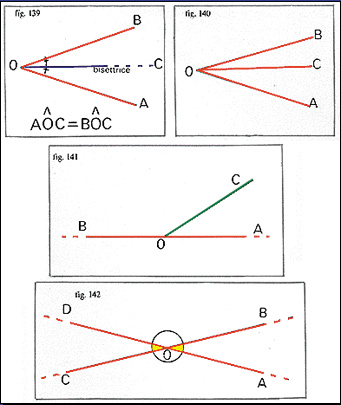
Più in generale, ogni semiretta che ha origine nel vertice di un angolo e che lo divide in due angoli uguali si chiamerà bisettrice dell'angolo (fig. 139).
Si dirà infine che:
- due angoli AôC e BôC sono consecutivi quando hanno in comune un vertice e un lato (fig. 140).
- due angoli AôC e BôC sono adiacenti quando sono consecutivi e hanno i due lati non in comune che giacciono sulla stessa retta (fig. 141).
- due angoli AôB e CôD sono opposti al vertice quando sono ottenuti prolungando l'uno i lati dell'altro, e hanno quindi il vertice in comune e i lati giacenti sulle stesse due rette (fig. 142).
CONFRONTO E OPERAZIONI FRA ANGOLI
Quanto è stato detto nel capitolo precedente circa la possibilità di spostare i segmenti sul piano senza che si deformino può anche essere esteso al caso degli angoli.Infatti, dati due angoli AôB e A'ôB', potete sovrapporli in modo tale che abbiano un lato e il vertice in comune.
Si potranno presentare allora tre casi:
a) Coincidono anche i lati OB e OB';
si dice allora che i due angoli sono uguali:
AôB = A'ôB'.
b) Il lato OB' cade interamente all'angolo AôB;
si dice allora che AôB è maggiore di A'ôB': AôB > A'ôB'.
c) Il lato OB' cade esternamente all'angolo AôB;
si dice allora che AôB è minore di A'ôB': AôB A'ôB'.
Un angolo maggiore di un angolo retto (ma minore di un angolo piatto) è chiamato ottuso.
Un angolo minore di un angolo retto si chiama invece acuto. Come sui segmenti, anche sugli angoli si possono eseguire le seguenti operazioni:
1) somma di angoli.
Se gli angoli AôB e CôB sono consecutivi, l'angolo AôC è detto somma dei due angoli consecutivi:
AôC = AôB + BôC.
Operando in questo modo si possono sommare anche angoli non consecutivi e in numero maggiore di due:
basta infatti costruire ogni volta il consecutivo della somma degli altri angoli svolta in precedenza.
2) differenza di angoli.
Se sovrapponete due angoli AôB e CôD facendo coincidere AO e CO, l'angolo BôD che sommato all'angolo AôB dà CôD è detto la differenza dei due angoli sovrapposti:
BôD = CôD - AôB.
3) moltiplicazione di angoli.
Se dato un angolo AôB, sommate un certo numero di angoli tutti uguali ad AôB otterrete un angolo multiplo di AôB secondo quel numero:
AôB = BôC = AôD = DOE quindi CôE = 4AôB.
4) divisione di angoli.
Nel disegno precedente potete constatare che AôB è contenuto in CôE un ben determinato numero di volte:
nel nostro caso, esattamente quattro volte.
Si dice allora che AôB è il sottomultiplo di CôE secondo il numero quattro:
CôE
AôB = ---
4
Nozioni molto importanti sono quelle di angolo supplementare e angolo complementare.
Due angoli sono supplementari quando, sommati, danno un angolo piatto.
Due angoli invece sono complementari quando, sommati, danno un angolo retto.
Gli angoli supplementari godono della seguente proprietà:
- angoli supplementari di uno stesso angolo sono uguali.
(Infatti se da un angolo piatto sottraete sempre lo stesso angolo otterrete angoli uguali).
Allo stesso modo vale la proprietà che:
- angoli complementari di uno stesso angolo sono uguali.
(Come nel caso precedente infatti, la sottrazione dello stesso angolo da un angolo retto dà sempre lo stesso risultato).
RETTE PERPENDICOLARI E RETTE PARALLELE
Due linee rette che si incontrano formando quattro angoli retti si dicono rette perpendicolari.Come esempio di rette perpendicolari immaginate il periscopio di un sommergibile.
Molto importante è la seguente proprietà:
- per un punto passa una sola perpendicolare a una retta data.
Vi potete rendere conto di ciò usando una riga e una squadra.
Data infatti una retta r e un punto O fuori di essa, fate coincidere l'orlo graduato della riga con la retta r;
quindi fate scorrere lungo la riga un lato dell'angolo retto della squadra in modo tale che l'altro lato dell'angolo retto raggiunga il punto 0.
Da questo punto disegnate la retta OH lungo il lato della squadra.
Immediatamente vi accorgerete allora che la costruzione porta sempre a tracciare la stessa retta OH.
Il segmento OH è chiamato distanza del punto O dalla retta r.
La perpendicolare a un segmento che taglia il segmento in due parti uguali, che passa cioè per il suo punto medio, è detta asse del segmento.
Le rette perpendicolari sono casi particolari di rette incidenti, poiché si incontrano sempre in un punto.
Pensate adesso alle corsie di una pista di atletica:
in questo caso le linee rette non si incontrano mai.
Ora, due rette che appartengono allo stesso piano e che non si incontrano mai si dicono parallele.
Nel caso che le rette parallele siano in numero maggiore di due bisogna parlare di fascio di rette parallele.
Il modo in cui sono state definite le parallele, cioè come rette che appartengono allo stesso piano e che non si incontrano mai, vi suggerisce che:
- dati su un piano una retta e un punto fuori di essa, per questo punto passa una sola parallela alla retta data (fig. 160).
L'unica retta passante per il punto O e che non incontra mai la retta r è infatti la retta t, mentre le altre rette la incontrano;
t è allora la sola parallela alla retta r.
Il segmento OH perpendicolare a entrambe le rette r e t si chiama distanza delle due rette parallele (fig. 161).
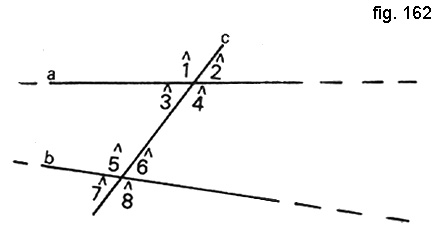
Disegnate ora due rette a e b sul piano.
Disegnate inoltre una terza retta c che interseca sia a che b (figura 162).
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
Come potete vedere, in questo modo otterrete otto angoli:
- gli angoli 3-6 e 4-5 sono detti angoli alterni interni.
- gli angoli 1-8 e 2-7 sono detti angoli alterni esterni.
- gli angoli 1-5,-2-6,3-7,4-8 sono detti angoli corrispondenti.
- gli angoli 3-5 e 4-6 sono detti angoli coniugati interni.
- gli angoli 1-7 e 2-8 sono detti angoli coniugati esterni.
Quando due rette parallele sono tagliate da una terza retta si ottengono:
- angoli alterni interni e angoli alterni esterni uguali
- angoli corrispondenti uguali
- angoli coniugati interni ed angoli coniugati esterni supplementari.
VERO O FALSO?
1) L'angolo è la figura formata da due semirette aventi la stessa origine e da ciascuna delle due parti in cui esse dividono il piano.2) Un angolo convesso può essere maggiore, minore o uguale a un angolo concavo.
3) L'angolo giro contiene tutti i punti del piano.
4) La bisettrice di un angolo è la semiretta che divide l'angolo in due parti uguali.
5) Date due rette parallele esiste un'unica perpendicolare alle rette date.
l) Vero.
2) Falso: è sempre minore.
3) Vero.
4) Falso: bisogna precisare che è la semiretta che ha origine nel vertice dell'angolo.
5) Falso: esistono infinite perpendicolari, anche se soltanto una per ciascun punto esterno alle rette date.
ESERCIZI
- Disegna le bisettrici degli angoli formati da due rette incidenti e dì come risultano fra loro.- Dato un angolo acuto, disegna l'angolo complementare e quello supplementare.
- Traccia le parallele a una data retta alla distanza di 4 cm.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()