Matematica Dizionario a b c d e f g i k l m n o p q r s t u v z
Dizionario di matematica e geometria iniziale T
TALETE, TEOREMA DI
Enunciato
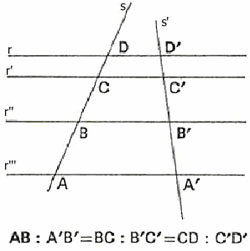
"Se un fascio di rette parallele è intersecato da due trasversali, a segmenti uguali sull'una corrispondono segmenti uguali sull'altra"
Costruzione geometrica
Disegniamo una retta r passante per un punto qualsiasi del piano; tracciamo tre qualsiasi rette parallele ad r. Chiamiamole r', r'' ed r'''; l'insieme delle quattro rette costituisce un fascio di rette parallele. Disegniamo ora due rette s ed s' trasversali (ovvero che tagliano il fascio di rette); detti A, B, C e D i punti di intersezione di s con il fascio, e A', B', C' e D i punti di intersezione di s', determiniamo sulle due rette le coppie di segmenti AB , BC, CD e A'B' , B'C', C'D'. Come è possibile verificare, se variamo l'inclinazione di una retta, s o s', il rapporto tra i segmenti staccati su quella retta rimane costante: le grandezze dei segmenti sono direttamente proporzionali e i rapporti tra le coppie di segmenti rimangono uguali tra loro al variare delle posizioni delle rette.Possiamo allora scrivere la proporzione:
AB : A'B' = BC : B'C' = CD : C'D'
TANGENTE
Una tangente in un punto M di una curva C è la posizione limite, se esiste, della secante MM', quando M', che è un altro punto di C, tende a M fino a coincidere con esso. Il punto M si dice allora il punto di contatto tra la curva e la sua tangente, o punto di tangenza.
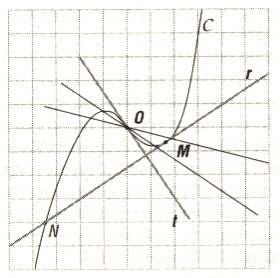
In trigonometria la tangente di un angolo è uno dei rapporti che servono a caratterizzarlo. La tangente di un angolo è definito come il rapporto tra il seno ed il coseno dello stesso angolo. Il nome della funzione deriva dal fatto che può esser definita come la lunghezza di un segmento della tangente (in senso geometrico) alla circonferenza goniometrica. Infatti, dato un cerchio di raggio unitario, la tangente corriponde alla lunghezza del segmento di retta tangente alla circonferenza compreso tra l'intersezione con l'asse X nel punto di tangenza e l'intersezione con il raggio vettore.
TEOREMA
In matematica per teorema si intende un enunciato che viene dimostrato nell'ambito di una teoria formale (come ogni altra proposizione derivabile dagli assiomi della teoria mediante un procedimento dimostrativo) e che in una esposizione sistematica della teoria viene presentato come risultato di rilievo. Il suo ruolo di rilievo differenzia i teoremi dai lemmi, dai corollari e dalle semplici proposizioni della teoria.Un teorema è quindi una affermazione di cui bisogna controllare la verità mediante un ragionamento. Talora si usa il termine "teorema" anche per un'affermazione per la quale non si dispone di una dimostrazione interamente soddisfacente, ma solo di una prova che copre una casistica ampia ma non esauriente o di una prova con qualche passaggio poco definito. Una tale affermazione si avvicina quindi a una congettura, affermazione che si ritiene valida sulla base di esempi e di considerazioni favorevoli, ma che manca ancora di una dimostrazione (e per la quale si usa anche, piuttosto impropriamente il termine "ipotesi").
TERNA
Una terna è un'insieme ordinato di tre elementi. Per esempio, si dirà che la terna (3, 4, 5) è una terna pitagorica, poiché, considerati in quest'ordine, questi tre numeri naturali, che possono essere intesi come le misure, rispetto a una certa unità, delle lunghezze dei lati di un triangolo rettangolo, dato che verificano il teorema di Pitagora: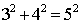
.
TETRAEDO
Un tetraedero è un poliedro con quattro facce, quattro vertici e sei spigoli; poiché tutte le sue facce sono triangoli, può essere considerato come una piramide a base triangolare.
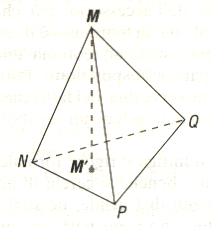
Un tetraedro regolare è una piramide le cui facce sono triangoli equilateri.
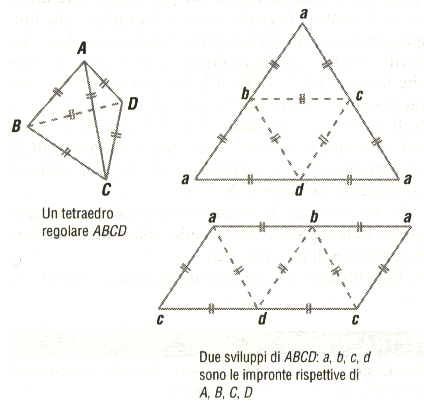
TORO
In geometria il toro è una superficie a forma di ciambella. Può essere ottenuta come superficie di rivoluzione, facendo ruotare una circonferenza (la generatrice) intorno ad un asse di rotazione, che appartiene allo stesso piano della generatrice, ma che è disgiunto da questa.
Proprietà
L'area ed il volume racchiuso dal toro sono dati rispettivamente da:
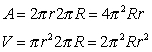
TRANSITIVO
Una relazione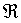
in un insieme I si dice transitiva quando, tutte le volte che a e
b sono associati nella relazione, e così pure b e c, anche
a e c
sono associati. In altre parole:per ogni coppia 
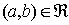
e ogni coppia
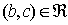
si ha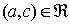 
.
TRAPEZIO
Un trapezio è un quadrilatero convesso particolare avente due lati parralleli, detti basi, di lunghezza diversa. L'altezza è la distanza fra le rette parallele a cui appartengono le due basi. Se i suoi due lati non paralleli hanno la medesima lunghezza, il trapezio è isoscele. Se ha due angoli retti, il trapezio è detto rettangolo. Il perimetro del trapezio si calcola facendo la somma delle lunghezze dei lati.L'area si può ottenere in due modi:
- come la metà di quella di un parallelogramma costruito attaccando al trapezio dato un trapezio con le stesse dimensioni
- come quella di un rettangolo ottenuto tagliando opportunamente il trapezio e riaggiungendo i pezzi tagliati; la lunghezza della base del rettangolo è quella del segmento MN, segmento congiungente i punti medi dei lati non paralleli, ed è uguale alla semisomma delle lunghezze delle basi del trapezio
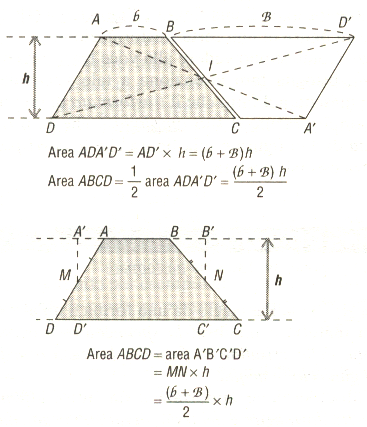
Se b, B e h designano le lunghezze delle due basi e dell'altezza di un trapezio, la sua area A è uguale al semiprodotto della somma delle basi per l'altezza (o al prodotto della semisomma delle basi per l'altezza):
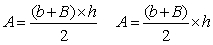
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
TRIANGOLO.
In matematica, il triangolo è un poligono con tre vertici la cui somma degli angoli interni nella geometria piana è sempre uguale a 180°. Esso rappresenta anche il poligono più semplice in quanto 3 è il numero minimo di lati necessari per delimitare un'area chiusa di superficie.Caratteristiche
In ogni triangolo valgono le seguenti proprietà:- la somma degli angoli interni è uguale ad un angolo piatto (180°);
- ciascun angolo esterno è uguale alla somma dei due angoli interni non adiacenti;
- almeno due angoli interni sono acuti;
- non è possibile che più di un angolo interno sia retto od ottuso;
I tre criteri di uguaglianza dei triangoli
Due triangoli si dicono simili se soddisfano almeno uno dei criteri di similitudine.
I tre criteri di similitudine dei triangoli
Tipi di triangolo
I triangoli possono essere classificati in base alla lunghezza dei lati:In un triangolo equilatero tutti i lati hanno lunghezza uguale. Un triangolo equilatero è anche equiangolare, ovvero i suoi angoli interni sono tutti pari a 60°. In un triangolo isoscele due lati hanno lunghezza uguale. Un triangolo isoscele ha anche due angoli interni uguali. In un triangolo scaleno tutti i lati hanno lunghezze differenti. Gli angoli interni di un triangolo scaleno sono tutti differenti.
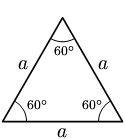
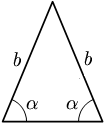
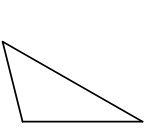
Equilatero Isoscele Scaleno
I triangoli possono essere classificati anche in base alle dimensioni del loro angolo interno più ampio; sono descritti di seguito usando i gradi d'arco. Un triangolo rettangolo (o triangolo retto) ha un angolo interno di 90° (un angolo retto). Il lato opposto all'angolo retto è detto ipotenusa; è il lato più lungo del triangolo rettangolo. Gli altri due lati del triangolo sono detti cateti. Un triangolo ottusangolo (o triangolo ottuso) ha un angolo interno maggiore di 90° (un angolo ottuso). Un triangolo acutangolo (o triangolo acuto) ha tutti gli angoli interni minori di 90° (tre angoli acuti).
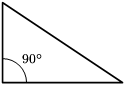
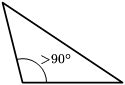
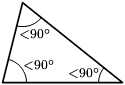
Rettangolo Ottusangolo Acutangolo
Punti Notevoli
Ad ogni triangolo sono associati vari punti, ciascuno dei quali svolge un ruolo che, per qualche aspetto, lo qualifica come centrale per il triangolo stesso. Definiamo concisamente questi punti riferendoci ad un triangolo T i cui vertici denotiamo con A, B e C e i cui lati opposti denotiamo rispettivamente con a, b e c.- ortocentro di T è l'intersezione delle sue altezze;
- baricentro (geometria) o centroide di T è l'intersezione delle sue mediane;
- incentro di T è l'intersezione delle sue tre bisettrici, ovvero il centro dell'incerchio di T;
- circocentro di T è il centro della sua circonferenza circoscritta;
- excentro di T opposto a un suo vertice A è l'intersezione della sua bisettrice in A e delle due bisettrici esterne relative ai due vertici rimanenti B e C;
- punto di Bevan di T è il circocentro del triangolo excentrale di T;
- punto di Apollonio di T è l'intersezione dei tre segmenti che rispettivamente uniscono un vertice A di T con il punto nel quale l'excerchio di T opposto ad A è tangente al cerchio tangente ai tre excerchi di T;
- punto di Gergonne di T è l'intersezione dei tre segmenti che rispettivamente uniscono un vertice A di T con il punto nel quale il lato di T opposto ad A è tangente dell'incerchio di T;
- punto di Nagel di T è l'intersezione dei tre segmenti ciascuno dei quali unisce un vertice di T con il punto nel quale il suo lato opposto è tangente del corrispondente excerchio;
- punto di Fermat di T è l'intersezione dei tre segmenti ciascuno dei quali unisce un vertice A di T con il vertice non appartenente a T del triangolo equilatero uno dei cui lati è il lato a opposto ad A ed esterno a T;
- punto di Napoleone di T è l'intersezione dei tre segmenti ciascuno dei quali unisce un vertice A di T con il centro del triangolo equilatero uno dei cui lati è il lato a opposto ad A ed esterno a T;
- centro dei nove punti di T è il centro del cosiddetto cerchio dei nove punti di T; questi nove punti comprendono i tre punti medi dei lati di T, i tre piedi delle altezze di T, i punti medi dei tre segmenti ciascuno dei quali unisce un vertice di T con l'ortocentro di T.
Formule geometriche
Area
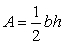
L'area di un triangolo è la metà di un rettangolo avente la stessa base (b) e la stessa altezza (h), come da figura, ovvero è uguale al semiprodotto di un generico lato per la relativa altezza.
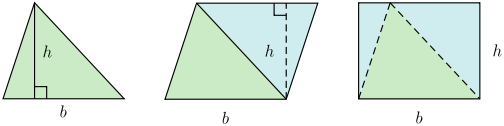
Il triangolo viene trasformato in un parallelogramma con area doppia rispetto a
quella del triangolo, quindi in un rettangolo
Perimetro
P = a + b + cAltezza del lato x
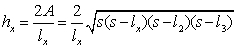
TRIANGOLO EQUILATERO
Un triangolo equilatero è un triangolo con tutti i lati congruenti e dunque è il poligono regolare con tre lati. Gli angoli sono tutti uguali e pari a 60°. I triangoli equilateri sono particolari triangoli isosceli. Tutti i triangoli equilateri sono simili tra di loro: per caratterizzare metricamente un triangolo equilatero, ovvero per caratterizzare la classe dei triangoli equilateri nel piano ottenibili gli uni dagli altri mediante traslazioni e rotazioni, serve e basta un parametro estensivo; tipicamente si usa la lunghezza dei suoi lati.
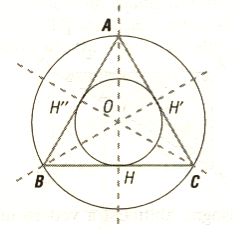
Formule
Indicando con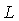
il lato del triangolo si ha:
TRIANGOLO ISOSCELE
Si definisce triangolo isoscele un triangolo che possiede almeno due lati uguali o equivalente un triangolo che possiede almeno due angoli uguali. Infatti vale il seguente teorema: "un triangolo ha due lati uguali se e solo se ha due angoli uguali". Particolari triangoli isosceli sono i triangoli equilateri e i triangoli rettangoli isosceli. Esistono anche triangoli isosceli acutangoli e ottusangoli. I triangoli isosceli rettangoli sono tutti simili tra di loro, come i triangoli equilateri. Un triangolo isoscele ha gli angoli alla base congruenti. In un triangolo isoscele l'altezza, la mediana, l'asse relativi alla base e la bisettrice dell'angolo al vertice coincidono.
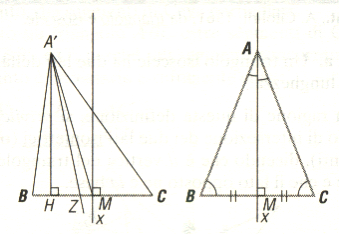
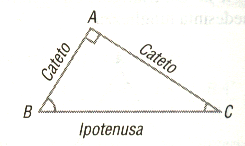
TRIANGOLO RETTANGOLO
Un triangolo rettangolo è un triangolo avente un angolo retto; i suoi angoli acuti sono, quindi, complementari. Il lato opposto all'angolo retto si dice ipotenusa, gli altri due lati si dicono cateti.
In un triangolo rettangolo, la mediana relativa all'ipotenusa è uguale alla metà
dell'ipotenusa stessa. Ogni triangolo inscritto in una semicirconferenza è
rettangolo.
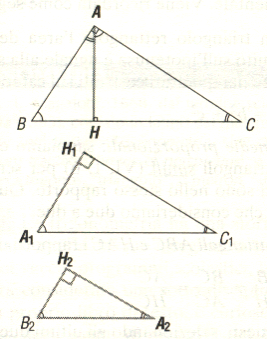
Una qualunque perpendicolare a uno dei lati di un triangolo rettangolo condotta da un punto del lato stesso determina un nuovo triangolo rettangolo, che è una riduzione del primo. L'altezza relativa all'ipotenusa individua in un triangolo rettangolo due triangoli a esso simili e che ne sono la riduzione.
TRIANGOLO RETTANGOLO ISOSCELE
Un triangolo rettangolo isoscele riunisce le due caratteristiche di "rettangolo" e di "isoscele": ha dunque un angolo retto e due lati della stessa lunghezza.TRIGONOMETRIA
La geometria elementare ci insegna a costruire un triangolo, dati tre elementi, di cui almeno uno sia un lato. Costruito così il triangolo, la geometria non ci permette, in generale, di determinare con l'approssimazione desiderata, le misure degli elementi del triangolo. Viene allora spontaneo vedere se è possibile trovare un procedimento di calcolo che ci permette di determinare, con l'approssimazione che si desidera, la misura degli elementi di un triangolo, noti che siano alcuni di essi. Tale problema è risolto dalla Trigonometria.I compiti specifici
Il compito principale della trigonometria consiste nel calcolare le misure che caratterizzano gli elementi di un triangolo (lati, angoli, mediane) partendo da altre misure già note (almeno tre, di cui almeno una lunghezza), per mezzo di speciali funzioni. Tale compito è indicato come risoluzione del triangolo. È anche possibile servirsi di calcoli trigonometrici nella risoluzione di problemi correlati a figure geometriche più complesse, come poligoni o figure geometriche solide, ed in molti altri rami della matematica.Funzioni trigonometriche
Strumento indispensabile della trigonometria sono le funzioni trigonometriche. Sono queste funzioni che associano lunghezze ad angoli, e viceversa. Le tabelle in questa sezione mostrano le funzioni trigonometriche insieme alle loro principali proprietà. Per ulteriori caratteristiche consultare la voce relativa ad una funzione.Funzioni trigonometriche dirette
Sono dette funzioni trigonometriche dirette quelle che associano una lunghezza o un rapporto fra lunghezze ad un angolo, solitamente espresso in radianti. A causa dell'equivalenza circolare degli angoli, tutte le funzioni trigonometriche dirette sono anche funzioni periodiche con periodo π o 2π.|
Funzioni trigonometriche dirette |
||||||
|
Funzione |
Notazione |
Dominio |
Codominio |
Radici |
Periodo |
Funzione inversa |
|
seno |
sin, sen |
 |
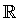[-1,1] |
 |
 |
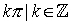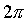arcoseno |
|
coseno |
cos |
|
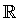[-1,1] |
 |
|
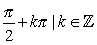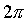arcocoseno |
|
tangente |
tan, tg |
 |
|
|
 |
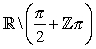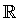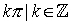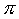arcotangente |
|
cotangente |
cot, cotg, ctg |
 |
|
|
|
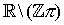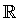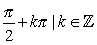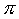arotangente |
|
secante |
sec |
|
 |
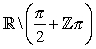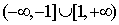nessuna |
|
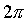arcosecante |
|
cosecante |
csc |
|
|
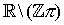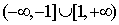nessuna |
|
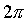arcocosecante |
Funzioni trigonometriche inverse
Ad ogni funzione trigonometrica diretta è associata una funzione inversa. Il dominio di ciascuna funzione trigonometrica inversa corrisponde com'è prevedibile al codominio della rispettiva funzione diretta. Poiché le funzioni dirette sono tuttavia periodiche e perciò non iniettive, per poterle invertire è necessario restringerne il dominio rendendole biiettive. La scelta della restrizione è teoricamente irrilevante e le possibilità sono infinite. La convenzione (rigida in questo campo) vuole però che i domini vengano ristretti agli intervalli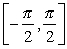
oppure
,
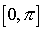in cui la funzione - e dunque anche la sua inversione - siano monotone.
Anche le funzioni arcosecante ed arcocosecante il cui domini non sono continui
vengono definite dall'inversione delle funzioni dirette ristrette ad uno di tali
intervalli.
|
Funzioni trigonometriche inverse |
||||||
|
Funzione |
Notazione |
Dominio |
Codominio |
Radici |
Andamento |
Funzione diretta |
|
arcoseno |
arcsin, arcsen, sin-1 |
 |
|
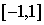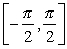0 |
 |
seno |
|
arcocoseno |
arccos, cos-1 |
|
 |
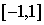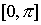1 |
 |
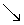coseno |
|
arcotangente |
arctan, arctg, tan-1 |
|
|
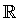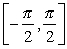0 |
|
tangente |
|
arcocotangente |
arccot, arccotg, arcctg, cot-1 |
|
|
 |
|
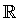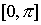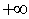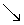cotangente |
|
arcosecante |
arcsec, sec-1 |
|
|
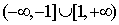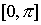1 |
discontinuo |
secante |
|
arcocosecante |
arccsc, csc-1 |
|
|
 |
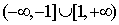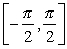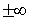discontinuo |
cosecante |
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
