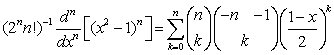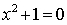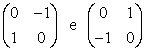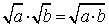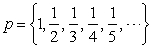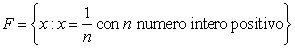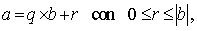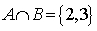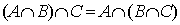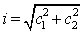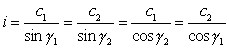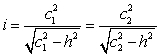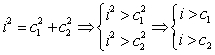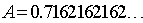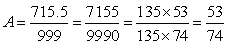![]()
![]()
Dizionario di matematica e geometria iniziale I
I
IDENTITÀ
In matematica, si dice identità un'uguaglianza tra due espressioni nelle quali intervengono una o più variabili, la quale è verificata per tutti i valori che si possono attribuire alle variabili stesse, con il solo vincolo di rendere sensate le espressioni.Viene enunciata mediante identità una gran parte dei risultati della matematica (teoremi, lemmi, corollari), delle ipotesi, delle condizioni, dei vincoli e delle affermazioni che sono solo allo stadio delle congetture.
Verificare un'identità significa calcolare il primo e il secondo membro indipendentemente, senza spostare alcun termine da un membro all'altro come invece accade nel calcolo di una normale equazione. L'identità è verificata se al primo e secondo membro resta lo stesso valore numerico.
Esempi di identità
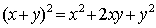
è un'identità dell'algebra elementare.
è un'identità trigonometrica.
è un'identità concernente il polinomio di Legendre di grado n
IMMAGINARIO
In matematica l' unità immaginaria i (a volte rappresentata dalla lettera j o dalla lettera greca iota) permette di estendere il sistema dei numeri reali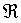 al
sistema dei numeri complessi
al
sistema dei numeri complessi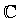 . La sua esatta definizione dipende dal
particolare metodo utilizzato per l'estensione.
. La sua esatta definizione dipende dal
particolare metodo utilizzato per l'estensione.La motivazione primaria per questa estensione consiste nel fatto che non tutte le equazioni polinomiali f(x) = 0 hanno una soluzione nei numeri reali. In particolare l'equazione x2 + 1 = 0 non ha soluzioni reali. Ma, se si considerano i numeri complessi, allora quella equazione, e in effetti tutte le equazioni polinomiali f(x) = 0 hanno almeno una.
Definizione
Per definizione, l'unità immaginaria i è una soluzione dell'equazioneLe operazioni sui numeri reali possono essere estese ai numeri immaginari e complessi considerando i come una quantità incognita durante la manipolazione delle espressioni, e poi usando la definizione per sostituire i2 con −1.
i e −i
L'equazione x2 + 1 = 0 ha, in effetti, due soluzioni distinte che sono opposte. Più precisamente, una volta che è stata fissata una soluzione i dell'equazione, allora −i (≠ i) è anch'essa una soluzione. Dato che l'equazione stessa è l'unica definizione per i, sembra che questa definizione sia ambigua (più precisamente, non sia ben definita). Però non si ha alcuna ambiguità una volta che si sceglie una soluzione e la si fissa, indicandola con i "positivo".Questa considerazione è sottile. Una spiegazione più precisa
consiste nell'affermare che, sebbene il campo complesso definito come 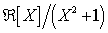 è unico a meno di isomorfismi, esso non è
unico a meno di un unico isomorfismo - esistono esattamente 2
automorfismi di
è unico a meno di isomorfismi, esso non è
unico a meno di un unico isomorfismo - esistono esattamente 2
automorfismi di 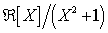 , l'identità e l'automorfismo che manda
X in −X. Si noti che questi non sono solo gli unici automorfismi
del campo
, l'identità e l'automorfismo che manda
X in −X. Si noti che questi non sono solo gli unici automorfismi
del campo 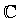 , ma sono gli unici automorfismi del campo
, ma sono gli unici automorfismi del campo
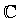 che tengono fisso qualunque numero reale. Si vedano le voci
complesso coniugato e gruppo di Galois.
che tengono fisso qualunque numero reale. Si vedano le voci
complesso coniugato e gruppo di Galois.
Un problema simile si ha se i numeri complessi vengono interpretati come matrici reali 2 × 2, perché entrambe le seguenti matrici
sono soluzioni dell'equazione x2 = −1. In questo caso l'ambiguità è dovuta alla scelta che si fa riguardo a quale sia la "direzione positiva" con cui viene percorso la circonferenza unitaria.
Avvertenza
Talvolta l'unità immaginaria viene scritta come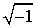 , ma bisogna fare molta attenzione quando si
manipolano formule che contengono radicali. Questa notazione è riservata alla
funzione radice quadrata principale, che è definita solo per numer reali x
≥ 0, o alla parte principale della funzione radice quadrata complessa.
L'applicazione delle proprietà delle radici quadrate principali (reali) al ramo
principale delle radici quadrate complesse produce risultati scorretti:
, ma bisogna fare molta attenzione quando si
manipolano formule che contengono radicali. Questa notazione è riservata alla
funzione radice quadrata principale, che è definita solo per numer reali x
≥ 0, o alla parte principale della funzione radice quadrata complessa.
L'applicazione delle proprietà delle radici quadrate principali (reali) al ramo
principale delle radici quadrate complesse produce risultati scorretti:
La regola
è valida solo per valori di a e b reali e non negativi.
Per evitare di fare errori nel manipolare i numeri complessi la strategia migliore è quella di non usare mai un numero negativo sotto a un segno di radice quadrata che non è preceduto da ±, in modo da far intendere che vengono considerate entrambe le radici.
Potenze di i
Le potenze di i si ripetono periodicamente:
i − 3 = i
i − 2 = − 1
i − 1 = − i
i0 = 1
i1 = i
i2 = − 1
i3 = − i
i4 = 1
i5 = i
i6 = − 1
Questa proprietà può essere espressa in forma più compatta in questo modo, dove n è un qualunque intero:
i4n = 1
i4n + 1 = i
i4n + 2 = − 1
i4n + 3 = − i
i e la formula di Eulero
Prendendo la formula di Eulero eix = cosx + isinx, e sostituendo π / 2 al posto di x, si ottiene
eiπ / 2 = i
Se entrambi i membri dell'uguaglianza vengono elevati alla potenza i, ricordando che i2 = − 1, si ottiene l'identità
In effetti è facile trovare che ii ha un infinito numero di soluzioni nella forma di
ii = e − π / 2 + 2πN
dove N è un qualunque intero. Dal punto di vista della teoria dei
numeri, i è un numero irrazionale quadratico, come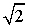 , e applicando il teorema di Gelfond - Schneider
si può concludere che tutti i valori ottenuti sopra, e in particolare e
− π / 2, sono trascendenti.
, e applicando il teorema di Gelfond - Schneider
si può concludere che tutti i valori ottenuti sopra, e in particolare e
− π / 2, sono trascendenti.
Dalla identità ottenuta precedentemente
eiπ / 2 = i
si arriva elegantemente all'identità di Eulero:
eiπ + 1 = 0,
che mette in relazione cinque delle più significative entità matematiche, assieme al principio di uguaglianza e le operazioni di addizione, moltiplicazione e potenza, in una semplice espressione.
![]()
![]()
INCIDENTI
Due o più rette incidenti o concorrenti sono rette che hanno un punto comune, che è il loro punto di intersezione. Si dirà, per esempio, che tre rette distinte r, s, t hanno il punto O in comune, o che sono incidenti in O, o che concorrono in O.INCLUSIONE
Nella teoria degli insiemi si parla più propriamente di inclusione stretta per indicare che ogni elemento di un insieme è anche elemento di un altro insieme. In altre parole, B è incluso strettamente in A se tutti gli elementi di B sono contenuti in A ma esistono elementi di A che non sono elementi di B.INCOGNITA
Le equazioni sono nate come strumenti per risolvere problemi, e lo sono tuttora: per questo si parla di "incognite". Che si tratti di equazioni o di disequazioni, coninuiamo a usare la designazione tradizionale "...a una incognita", "variabile": infatti quello che si conosce di questa incognita è che essa rappresenta una quantità che varia in un insieme dato. Inoltre quando per esempio si scrive x=3, questa è ancora un'equazione e non si dovrebbe intendere "x è uguale a 3", ma "la variabile x può prendere, in un certo momento, il valore 3", o più semplicemente "x può essere uguale a 3"; si vede che la nozione di incognita non interviene come tale poiché allora si ha solo un'equazione "trasparente", cioè messa in forma leggibile.INDICE
In matematica la notazione con un indice permette di dare indicazioni che completano la notazione principale, per esempio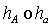 per l'altezza relativa al vertice A o al
lato
a;
per l'altezza relativa al vertice A o al
lato
a; 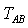 per latraslazione che porta A in B.
Con una notazione un po' diversa,
per latraslazione che porta A in B.
Con una notazione un po' diversa, 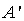 (leggere "A primo"),
(leggere "A primo"),
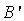 ecc., si indicano i trasformati dei punti A, B
ecc. in una trasformazione.
ecc., si indicano i trasformati dei punti A, B
ecc. in una trasformazione.INFINITO
L'infinito (dal latino "finitus", cioè limitato con prefisso negativo in-, e solitamente denotato dal simbolo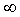 ) è la qualità di ciò che non ha limiti.
) è la qualità di ciò che non ha limiti.Il
concetto matematico di infinito ha la sua naturale collocazione nella teoria
degli insiemi: un insieme A si dice infinito se ogni suo sottoinsieme
finito è un sottoinsieme proprio. Una definizione alternativa è la seguente: un
insieme A è infinito se esiste un'applicazione biunivoca di A in
un suo sottoinsieme proprio
A'. In altre parole, A è infinito se e solo se è equivalente a un
suo sottoinsieme proprio.
È possibile fare una distinzione tra differenti
gradi di infinità dal momento che possono essere individuati insiemi infiniti
che hanno una cardinalità più grande degli altri. Georg Cantor sviluppò la
teoria dei numeri cardinali transfiniti, in cui il primo numero transfinito è
aleph-zero 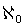 ,
che corrisponde alla cardinalità dell'insieme dei numeri naturali. Il successivo
grado di infinito noto è
,
che corrisponde alla cardinalità dell'insieme dei numeri naturali. Il successivo
grado di infinito noto è 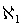 .
L'infinito corrispondente alla cardinalità dei numeri reali viene generalmente
indicato con
c. Il problema se
.
L'infinito corrispondente alla cardinalità dei numeri reali viene generalmente
indicato con
c. Il problema se 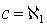 , vale a dire dell'esistenza o meno di una
cardinalità intermedia tra queste due, è la cosiddetta ipotesi del continuo.
, vale a dire dell'esistenza o meno di una
cardinalità intermedia tra queste due, è la cosiddetta ipotesi del continuo.
Nel 1940 Kurt Gödel dimostrò che tale ipotesi è coerente con gli assiomi di
Zermelo - Fraenkel (con o senza l'assioma della scelta); nel 1963 Paul Cohen ha
poi dimostrato che anche la negazione di tale ipotesi è coerente con quegli
assiomi; il risultato finale è che l'ipotesi del continuo non è né dimostrabile
né refutabile.
Cantor sviluppò anche la teoria dei numeri ordinali
transfiniti, che generalizzano agli insiemi infinti la nozione di ordinamento e
di posizione di un elemento all'interno di un ordinamento.
Una menzione a parte merita l'analisi non standard, introdotta da Abraham Robinson nel 1966: al contrario dell'analisi matematica comune, in essa gli infiniti (indicati con Ω) e infinitesimi (ε) hanno piena cittadinanza tra i numeri, e assieme ai reali formano i numeri iperreali. Ad esempio 1 e 1+ε sono numeri distinti. Al contrario dei numeri complessi, è possibile un ordinamento dei numeri iperreali grazie al concetto di ultrafiltro. L'analisi non standard è perfettamente coerente, e anzi semplifica molti teoremi sia di calcolo infinitesimale che di teoria dei numeri.
Un esempio è il teorema di Goodstein, che può essere risolto solamente mediante le proprietà degli ordinali transfiniti, mentre non è dimostrabile con i soli assiomi di Peano.
In topologia, l'insieme reale esteso è l'unione dei numeri reali con due
punti, indicati con 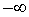 e
e 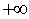 .
In simboli:
.
In simboli:
La relazione d'ordine si estende a questi nuovi punti ponendo:
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
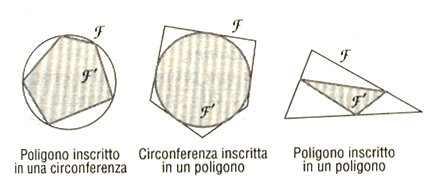
INSCRITTIBILE
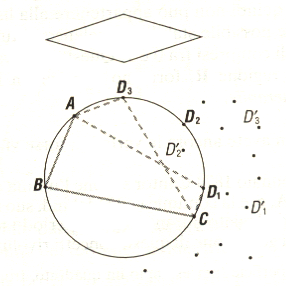
Inscrittibile significa "che può essere inscritto". Di solito ci si riferisce all'inscrizione di un poligono in una circonferenza o viceversa.Tipi di figure che possono essere inscrittibili: i quadrilateri
Un triangolo è sempre inscrittibile in una circonferenza (che ha centro nel punto di intersezione degli assi dei lati). Per un quadrilatero questo non è vero, come ci fa capire un rombo che non sia un quadrato.Per tre punti non allineati passa comunque una circonferenza, il problema si pone per il quarto vertice: solo per alcune posizioni di questo il quadrilatero risulta inscrittibile.
Condizioni affinché un quadrilatero sia inscrittibile
Le condizioni si esprimono di solito mediante gli angoli del quadrilatero, ma ve ne sono altre- Caratterizzazione mediante gli angoli. Un quadrilatero convesso è inscrittibile se e solo se gli angoli opposti sono supplementari. Un quadrilatero intrecciato è inscrittibile quando due angoli non consecutivi sono congruenti.
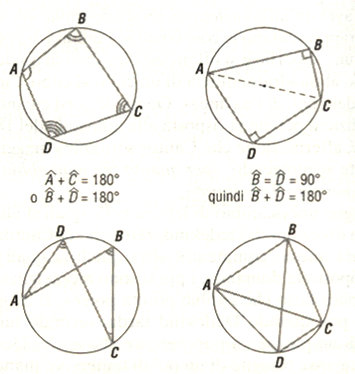
- Caratterizzazione mediante le lunghezze dei lati e delle diagonali. Un quadrilatero convesso è inscrittibile se e solo se la somma dei prodotti delle lunghezze dei lati opposti è uguale al prodotto delle lunghezze delle diagonali.
INSCRIVERE, INSCRITTO
Se F è una circonferenza, inscrivere in F un poligono F' significa costruire un poligono i cui vertici stanno su F.Se F è un poligono,
una circonferenza è inscritta in F se tutti i lati di F sono tangenti alla circonferenza;
si può parlare anche di un poligono F' inscritto in F, quando i vertici di F' stanno sui lati di F.
INSIEME
Il concetto di insieme costituisce l'elemento fondante di tutta la matematica moderna: qualunque testo introduttivo e qualunque area della matematica inizia con nozioni di teoria degli insiemi.Con il termine insieme si indica una collezione di oggetti chiamati elementi dell'insieme. Gli elementi possono o esserci o non esserci, non ci sono vie di mezzo, non possono comparire più volte e non hanno un ordine di comparizione. Gli elementi caratterizzano univocamente l'insieme: due insiemi coincidono se e solo se hanno gli stessi elementi.
Il concetto di insieme è primitivo ed intuitivo.
"primitivo" perché non può essere derivabile da concetti più elementari,
"intuitivo" perché nasce spontaneamente nella nostra mente ed ivi ne è sepolto.
Descrizioni di insiemi
Un insieme viene indicato solitamente con le lettere maiuscole dell'alfabeto: A, B, C, Z, X ... e deve essere univocamente determinato.Un insieme può essere definito nei seguenti modi:
In forma tabulare o per elencazione: vengono elencati tutti gli elementi, in tal caso la convenzione comune è quella di scrivere l'elenco degli elementi tra parentesi graffe separati da virgole, ad esempio:
F = {rosa, giglio, geranio}questo tipo di definizione è utilizzabile solo nel caso di insiemi finiti, per gli insiemi infiniti si fa talvolta uso di puntini di sospensione laddove si ritiene che è evidente il modo in cui sono stati scelti gli elementi, ad esempio:
Per caratteristica o in estensione: come l'insieme di tutti gli oggetti che verificano una determinata proprietà P. In tal caso si usa la scrittura {x:P(x)} dove al posto di P(x) può comparire la descrizione di una particolare proprietà. Es. : F = { x : x è un fiore} (F è definito come l'insieme degli x tale che x è un fiore),
Operazioni tra insiemi
Le principali operazioni tra insiemi sono:L' unione di due insiemi A e B: si indica con A∪B ed è data dall'insieme formato da tutti gli elementi che appartengono all'insieme A o all'insieme B o a entrambi.
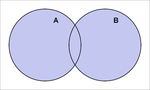
L' intersezione di due insiemi A e B: si indica con A∩B ed è data dall'insieme formato da tutti gli elementi che appartengono sia all'insieme A che all'insieme B contemporaneamente.
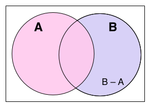
La differenza B meno A si indica con B\A o con B-A ed è data dall'insieme formato dai soli elementi di B che non appartengono ad A.
Cardinalità
Gli insiemi possono essere classificati in base al numero di elementi; in particolare un insieme èfinito: se ha un numero finito di elementi;
infinito: se ha infiniti elementi.
La cardinalità di un insieme lo caratterizza in base al numero dei suoi elementi.Due particolari tipi di insieme sono: l'insieme vuoto, cioè privo di
elementi, indicato con il simbolo 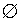 oppure ∅, o talvolta con "{}", la sua cardinalità è zero; e
l'insieme universo, cioè che contiene tutti gli insiemi esistenti (incluso anche
l'insieme vuoto), e che viene indicato con U.
oppure ∅, o talvolta con "{}", la sua cardinalità è zero; e
l'insieme universo, cioè che contiene tutti gli insiemi esistenti (incluso anche
l'insieme vuoto), e che viene indicato con U.
Graficamente gli insiemi si rappresentano con i diagrammi di Eulero/Venn.
INTERI (RELATIVI)
Gli interi relativi, detti semplicemente interi, sono gli elementi dell'insiemeVisti dalla parte dei numeri interi "ordinari" obbligano a distinguere questi ultimi chiamandoli numeri interi naturali o semplicemente numeri naturali; 3, 5, 20, 57 sono numeri naturali, +3, +20 sono numeri interi positivi, -5, -57 sono numeri interi negativi.
INTERO
I numeri interi sono formati dall'unione dei numeri naturali (0, 1, 2, ...) e dei numeri negativi (-1, -2, -3,...). L'insieme di tutti i numeri interi in matematica viene indicato con Z o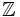 ,
perché è la lettera iniziale di "Zahl" che in tedesco significa numero.
,
perché è la lettera iniziale di "Zahl" che in tedesco significa numero.I numeri interi possono essere sommati, sottratti e moltiplicati e il risultato rimane un numero intero. L'inverso di un numero intero non è però un intero in generale, ma un numero razionale: i matematici esprimono questo fatto dicendo che Z è un anello commutativo ma non un campo.
Proprietà algebriche
Come i numeri naturali Z è chiuso rispetto alle operazioni di addizione e di moltiplicazione, cioè la somma o il prodotto di due interi è un intero. Inoltre, con l'inclusoine dei numeri naturali negativi e dello zero, Z (a differenza dei numeri naturali) è chiuso anche rispetto all'operazione di sottrazione: se a e b sono interi, anche a - b lo è. Tuttavia, Z non è chiuso sotto l'operazione di divisione, poiché il quoziente di due interi (per esempio 1/2) non è necessariamente un numero intero.La tabella seguente elenca alcune delle proprietà di base dell'addizione e della moltiplicazione per ogni intero a, b e c.
|
|
addizione |
moltiplicazione |
|
chiusura: |
a + b è un intero |
a × b è un intero |
|
proprietà associativa: |
a + (b + c) = (a + b) + c |
a × (b × c) = (a × b) × c |
|
proprietà commutativa: |
a + b = b + a |
a × b = b × a |
|
esistenza dell'elemento neutro: |
a + 0 = a |
a × 1 = a |
|
esistenz dell'elemento inverso: |
a + (−a) = 0 |
|
|
proprietà distributiva: |
a × (b + c) = (a × b) + (a × c) |
|
Gruppo
Nel linguaggio dell'algebra astratta, le prime cinque proprietà elencate sopra per l'addizione dicono che Z è un gruppo abeliano con l'operazione somma. In particolare, Z è un gruppo ciclico, poiché ogni intero non nullo può essere scritto sommando un certo numero di volte 1 + 1 + ... + 1 oppure (−1) + (−1) + ... + (−1). Il gruppo Z è l' unico gruppo ciclico infinito, nel senso che ogni altro gruppo ciclico infinito è isomorfo a Z.Anello
Le prime quattro proprietà elecante sopra per la moltiplicazione dicono che Z con l'operazione prodotto forma un monoide commutativo. Tuttavia, si nota che non tutti gli interi hanno in inverso rispetto alla moltiplicazione; per esempio non esiste un intero x tale che 2x = 1. Quindi Z non è un gruppo se considerato con l'operazione prodotto.Tutte le proprietà dalla tabella prese insieme dicono che Z con l'addizione e la moltiplicazione è un anello commutativo con unità. In effetti Z è la motivazione principale per la definizione di tale struttura. La mancanza dell'inverso rispetto alla moltiplicazione è tradotta nel fatto che Z non è un campo.
L'anello Z è inoltre un dominio d'integrità, perché non contiene divisori dello zero. Ogni dominio di integrità è contenuto in un campo, e il più piccolo campo contenente gli interi è il campo Q dei numeri razionali.
Algoritmo di Euclide
Anche se la divisione ordinaria non è definita su Z, è possibile usare l'algoritmo di Euclide per effettuare una divisione con resto: dati due interi a e b con b ≠ 0, esistono e sono unici due interi q e r tali chedove |b| è il valore assoluto di b. L'intero q è chiamato il quoziente e r è chiamato il resto, risultanti dalla divisione di a con b.
L'algoritmo di Euclide mostra come due numeri interi abbiano sempre un massimo comune divisore ed un minimo comune multiplo. Inoltre, per il teorema fondamentale dell'aritmetica ogni numero intero ha un'unica decomposizione come prodotto di numeri primi. L'esistenza dell'algoritmo di Euclide fa di Z un anello euclideo.
Ordinamento
Z è un insieme totalmente ordinato senza estremo superiore o inferiore. L'ordine di Z è dato da... < -2 <-1 < 0 < 1 < 2 < ...
Un numero intero è positivo se è maggiore dello zero e negativo se minore di zero; zero non è considerato un numero positivo né negativo.
L'ordine seguente è compatibile con le regole dell'algebra:
- se a < b e c < d, allora a + c < b + d
- se a < b e 0 < c, allora ac < bc
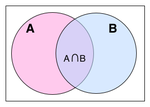
INTERSEZIONE
Nella teoria degli insiemi, l'intersezione di due insiemi A e B è data dall'insieme formato da tutti gli elementi che appartengono sia all'insieme A che all'insieme B contemporaneamente.Definizione
L'intersezione di due insiemi A e B si denota comunemente con "A ∩ B". Quindi x è un elemento di A ∩ B se e solo se x è un elemento di A e x è un elemento di B, in simboli:Naturalmente può accadere che tali elementi x non esistano, nel qual caso si dice che i due insiemi sono disgiunti, ovvero che l'intersezione dei due insiemi A e B è l'insieme vuoto, che si denota con il simbolo Ø.
Esempi
Come esempio elementare si possono considerare due insiemi finiti (cioè con un numero finito di elementi) A = {1, 2, 3} e B = {2, 3, 4}. In questo caso si può verificare direttamente per ogni elemento di A se è anche elemento di B (o vice versa), ottenendoUn esempio un po' più astratto è dato da due insiemi definiti tramite determinate proprietà dei loro elementi: Siano A l'insieme dei numeri interi divisibili per 4 e B l'insieme dei numeri interi divisibili per 6. In questo caso, A ∩ B è l'insieme dei numeri interi divisibili sia per 4 che per 6, ovvero tutti i numeri interi divisibili per 12.
Gli insiemi dei numeri pari e dei numeri dispari sono disgiunti; infatti un numero non può essere contemporaneamente pari e dispari. L'intersezione di questi due insiemi è quindi l'insieme vuoto.
Proprietà
Dalla definizione segue immediatamente che l'intersezione ¼ un'operazione commutativa, in simboli:L'intersezione è inoltre un'operazione associativa:
Per questo si può rinunciare alle parentesi quando si considera l'intersezione di più di due insiemi, scrivendo semplicemente A ∩ B ∩ C.
INTERVALLO
In matematica, un intervallo è un sottoinsieme dei numeri reali delimitato da due estremi a e b. Gli estremi possono (ma non devono) appartenere all'intervallo, e possono essere infiniti.Definizione
Formalmente, un sottoinsieme S dei numeri reali R o di un altro insieme ordinato è un intervallo se per ogni coppia di elementi x e y di S, ogni altro elemento z tale che x<z<y sta anch'esso in S.Gli intervalli di R sono quindi gli insiemi seguenti (dove a e b sono due numeri reali tali che a<b):
- (a,b) = { x | a < x < b } (intervallo aperto)
- [a,b] = { x | a ≤ x ≤ b } (intervallo chiuso)
- [a,b) = { x | a ≤ x < b } (intervallo chiuso a sinistra)
- (a,b] = { x | a < x ≤ b } (intervallo chiuso a destra)
- (a,∞) = { x | x > a } (intervallo aperto infinito a destra)
- [a,∞) = { x | x ≥ a } (intervallo chiuso infinito a destra)
- (-∞,b) = { x | x < b } (intervallo aperto infinito a sinistra)
- (-∞,b] = { x | x ≤ b } (intervallo chiuso infinito a sinistra)
- (-∞,∞) = R (tutta la retta reale)
- {a} (un punto)
- l'insieme vuoto
I primi quattro intervalli hanno lunghezza b - a, i cinque seguenti hanno lunghezza infinita, il punto e l'insieme vuoto hanno lunghezza zero.
Proprietà
L'unione e l'intersezione di due intervalli aventi intersezione non vuota è un intervallo.
Un sottoinsieme della retta reale è un intervallo se e solo se è connesso.
Un intervallo è compatto se e solo se è del tipo [a, b].
Ogni intervallo (anche infinito) è omeomorfo a uno (ed uno solo) di questi: un punto, [0, 1], [0, 1), (0, 1) o l'insieme vuoto.
INVERSO
In matematica due numeri a, a' si dicono inversi (l'uno dell'altro) quando il loro prodotto è 1. L'inverso del numero a è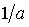 .
.L'inverso dell'inverso di un numero è il numero stesso.
Tutti i numeri razionali e reali, salvo lo zero, hanno inverso.
Non bisogna confondere tra inverso e opposto. Ecco allora una tabella esemplificativa.
|
Numero: a |
Opposto: -a |
Inverso: 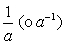 |
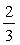 |
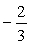 |
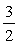 |
|
4 |
-4 |
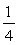 |
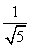 |
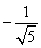 |
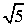 |
|
1 |
-1 |
1 |
|
-1 |
1 |
-1 |
IPOTENUSA
In un triangolo rettangolo si dice ipotenusa (dal latino hypotenusa dal greco hypoteínoysa, υποτείνουσα: linea tesa sotto) il lato opposto all'angolo retto. Gli altri due lati si chiamano invece cateti.Calcolo della lunghezza
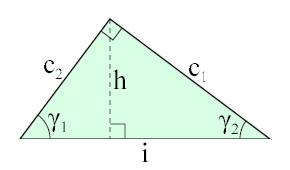
La relazione fondamentale fra i lati di un triangolo rettangolo è stabilita dal teorema di Pitagora, che può essere adoperato per calcolare la misura dell'ipotenusa quando sono note le misure dei cateti. Con i metodi della trigonometria è anche possibile determinare la misura dell'ipotenusa conoscendo la misura di uno solo dei cateti insieme all'ampiezza di uno degli angoli acuti del triangolo rettangolo.
Nelle formule riportate qui sotto indicheremo con i l'ipotenusa, con c1 e c2 i due cateti e con h l'altezza costruita sull'ipotenusa di un generico triangolo rettangolo. Gli angoli opposti ai cateti c1 e c2 saranno rispettivamente γ1 e γ2.
Dati i cateti
La misura dell'ipotenusa equivale alla radice quadrata della somma dei quadrati delle misure dei cateti. Questo enunciato è una conclusione diretta del teorema di Pitagora.
Dati un cateto e un angolo acuto
La misura dell'ipotenusa equivale a quella di un cateto divisa per il seno dell'angolo opposto al cateto, o per il coseno dell'angolo adiacente.
Dati un cateto e l'altezza sull'ipotenusa
La misura dell'ipotenusa di un triangolo rettangolo equivale al rapporto fra il quadrato della misura di un cateto e quella della proiezione del cateto stesso sull'ipotenusa. E poiché la proiezione di un cateto sull'ipotenusa forma a sua volta un triangolo rettangolo con il cateto e con l'altezza sull'ipotenusa, ecco le uguaglianze:
Dunque in un triangolo rettangolo poggiato sull'ipotenusa, la misura di questa è determinata in modo univoco da un cateto e dall'altezza.
Considerazioni
Con il teorema di Pitagora è facile dimostrare che la misura dell'ipotenusa è sempre maggiore di quella di un cateto. Ricordando che tutti i lati misurano più di zero:
Alla stessa conclusione si giunge applicando il teorema dei seni.
IPOTESI
Le ipotesi nell'ambito delle scienze sono la condizione stessa della loro elaborazione: esse generano il lavoro che permetterà, se sono verificate, di incorporarle in una teoria e di farle progredire, altrimenti di rigettarle e di cercarne delle altre.Ipotesi ha significati differenti a seconda che si tratti di quelle che sono contenute in un enunciato o di quelle che si fanno nel corso di una ricerca o di un tentativo di dimostrazione. Nel primo caso, si tratta di dati, con i quali si può lavorare in tutta sicurezza, per dimostrare un teorema o risolvere un problema.
Nel secondo caso, l'ipotesi è una supposizione che si può essere indotti a fare, e il seguito dirà se è vera: questo procedimento è, in particolare, usato nelle dimostrazioni dette per assurdo, nelle quali si vuole dimostrare che l'ipotesi che è stata fatta è falsa.
IRRAZIONALE
In matematica, un numero irrazionale è ogni numero reale che non è un numero razionale, cioè non può essere scritto come una frazione a / b con a e b interi, con b diverso da zero. La necessità dell'introduzione di questo insieme si rese evidente a causa dell'esistenza di grandezze incommensurabili, ossia prive di un sottomultiplo comune. I numeri irrazionali sono esattamente quei numeri la cui espansione in qualunque base (decimale, binaria, ecc) non termini mai e non formi una sequenza periodica. "Quasi tutti" i numeri reali sono irrazionali, in un senso che è definito più precisamente sotto.Alcuni
numeri irrazionali sono numeri algebrici come 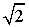 (la radice quadrata di due) e
(la radice quadrata di due) e 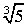 (la radice cubica di 5); altri sono numeri
trascendenti come π ed
e.
(la radice cubica di 5); altri sono numeri
trascendenti come π ed
e.
Storia della teoria dei numeri irrazionali
La scoperta dei numeri irrazionali viene tradizionalmente attribuita a Pitagora, o più precisamente al pitagorico Ippaso di Metaponto, che produsse una argomentazione (probabilmente con considerazioni geometriche) dell'irrazionalità della radice quadrata di 2. Secondo la tradizione Ippaso scoprì i numeri irrazionali mentre tentava di rappresentare la radice quadrata di 2 come frazione (vedi la dimostrazione sotto). Tuttavia Pitagora credeva nell'assolutezza dei numeri, e non poteva accettare l'esistenza dei numeri irrazionali. Egli non era in grado di confutare la loro esistenza con la logica, ma le sue credenze non potevano tollerarne l'esistenza e, secondo una leggenda un po' pulp, per questo condannò Ippaso a morire annegato.Qui occorre segnalare la piena capacità di trattare gli irrazionali dei matematici ellenistici.
Il sedicesimo secolo vide infine l'accoglienza favorevole da parte della comunità matematica dei numeri negativi, interi e frazionari. Il diciassettesimo secolo vide, da parte di matematici, l'uso sempre più frequente delle frazioni decimali con la notazione moderna. I successivi cento anni videro i numeri immaginari diventare un potente strumento nelle mani di Abraham de Moivre, e specialmente di Leonhard Euler. Per il diciannovesimo secolo rimase da completare la teoria dei numeri complessi, dimostrare l'esistenza dei numeri trascendenti, dividere gli irrazionali in algebrici e trascendenti, e compiere uno studio scientifico su un argomento che era rimasto quasi in letargo dai tempi di Euclide, la teoria degli irrazionali. L'anno 1872 vide la pubblicazione delle teorie di Karl Weierstrass (tramite il suo allievo Kossak), Eduard Heine (Crelle, 74), Georg Cantor (Annalen, 5), e Richard Dedekind. Méray aveva preso nel 1869 lo stesso punto di partenza di Heine, ma generalmente si attribuisce tale teoria all'anno 1872. Il metodo di Weierstrass fu completamente avviato da Pincherle (1880), e quello di Dedekind ricevette maggiore risalto tramite il successivo lavoro dell'autore (1888) e il più recente appoggio di Tannery (1894). Weierstrass, Cantor, e Heine basarono le loro teorie sulle serie infinite, mentre Dedekind, riallacciandosi a Euclide, fondò la sua sull'idea di un taglio (Schnitt) nel sistema dei numeri razionali, cioè nella bipartizione della totalità dei numeri razionali in due classi caratterizzate da proprietà contrastanti. L'argomento ricevette successivi contributi per mano di Weierstrass, Kronecker (Crelle, 101), e Méray.
Le frazioni continue, strettamente collegate ai numeri irrazionali (e dovute a Cataldi, 1613), furono prese in considerazione da parte di Eulero, e all'inizio del diciannovesimo secolo ebbero maggior rilievo grazie agli scritti di Joseph Louis Lagrange. Altri notevoli contributi furono dati da Druckenmüller (1837), Kunze (1857), Lemke (1870) e Günther (1872). Peter Ramus (1855) per la prima volta collegò l'argomento con i determinanti, dando vita, con i successivi contributi di Heine, August Ferdinand Möbius e Günther, alla teoria dei determinanti delle frazioni continue. Anche Dirichlet contribuì alla teoria generale.
I numeri trascendenti furono per la prima volta distinti dagli irrazionali algebrici da Kronecker. Lambert provò (1761) che π non può essere razionale, e che en è irrazionale se n è razionale (eccetto n = 0), dimostrazione, comunque, che lasciò molto a desiderare. Legendre (1794) completò la dimostrazione di Lambert, e mostrò che π non è la radice quadrata di un numero razionale. Joseph Liouville (1840) mostrò che né e né e2 possono essere radici di un'equazione quadratica intera. Ma l'esistenza di numeri trascendenti fu per la prima volta stabilita da Liouville (1844, 1851); la sua dimostrazione fu successivamente rimpiazzata da Georg Cantor (1873). Charles Hermite (1873) provò per primo la trascendenza di e, e Ferdinand von Lindemann (1882), partendo dalle conclusioni di Hermite, mostrò lo stesso per π. La dimostrazione di Lindemann fu molto semplificata da Weierstrass (1885), e ulteriormente da David Hilbert (1893); infine fu resa quasi elementare da Hurwitz e Gordan.
Irrazionalità di certi logaritmi
Forse i numeri che più facilmente si dimostra che siano irrazionali sono i logaritmi come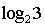 .
L'argomentazione tramite dimostrazione per assurdo è la seguente:
.
L'argomentazione tramite dimostrazione per assurdo è la seguente:Supponiamo
che
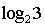 sia razionale. Allora esistono due interi
positivi m e n tali che
sia razionale. Allora esistono due interi
positivi m e n tali che
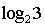 = m/n.
= m/n.
Di conseguenza 2m/n = 3.
Allora 2m = 3n.
Ma 2m è pari (perché almeno uno dei suoi fattori primi è 2) e 3n è dispari (perché tutti i suoi fattori sono uguali a 3), pertanto ciò è impossibile.
Irrazionalità della radice quadrata di 2
Una dimostrazione dell'irrazionalità della radice quadrata di 2 è la seguente, che procede per assurdo. La proposizione è provata assumendo l'opposto e mostrando che è falso, che implica che la proposizione iniziale debba essere vera.- Assumiamo che
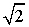 sia un numero razionale. Ciò comporta che
esistono due interi a e b tali che a / b =
sia un numero razionale. Ciò comporta che
esistono due interi a e b tali che a / b =
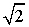 .
. - Allora
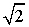 si può scrivere come una frazione irriducibile
a
/ b tale che a e b sono interi coprimi e (a /
b)2 = 2.
si può scrivere come una frazione irriducibile
a
/ b tale che a e b sono interi coprimi e (a /
b)2 = 2. - Segue che a2 / b2 = 2 ed a2 = 2b2.
- Dunque a2 è pari perché è uguale a 2b2 che è ovviamente pari.
- Segue che anche a deve essere pari. (Infatti numeri dispari hanno quadrati dispari e numeri pari hanno quadrati pari.)
- Poiché a è pari, esiste un intero k che soddisfa: a = 2k.
- Sostituendo otteniamo: 2b2 = (2k)2, cioè b2 = 2k2.
- Poiché 2k2 è pari segue che anche b2 è pari e quindi anche b è pari.
- In base alla (5) e la (8) a e b sono entrambi pari, che contraddice il fatto che a / b sia irriducibile come supposto nella (2).
Questa dimostrazione si può generalizzare per dimostrare che qualunque radice di qualunque numero naturale è un numero naturale o è irrazionale.
Una dimostrazione differente
Un'altra dimostrazione per assurdo che dimostra l'irrazionalità di 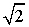 è meno conosciuta ma abbastanza interessante per essere inclusa qui. Essa
procede osservando che se
è meno conosciuta ma abbastanza interessante per essere inclusa qui. Essa
procede osservando che se 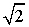 = m/n allora
= m/n allora 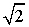 =
(2n − m)/(m − n), quindi una frazione ai minimi
termini viene ridotta in termini ancora minori. Questa è una contraddizione se
n e m sono interi positivi, dunque l'assuzione che
=
(2n − m)/(m − n), quindi una frazione ai minimi
termini viene ridotta in termini ancora minori. Questa è una contraddizione se
n e m sono interi positivi, dunque l'assuzione che 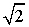 sia razionale deve essere falsa. Da un triangolo rettangolo
isoscele di cui i cateti e l'ipotenusa abbiano rispettivamente lunghezze n
e
m, tramite una classica costruzione con riga e compasso, e' possibile
costruire un triangolo isoscele rettangolo più piccolo tale che i cateti e
l'ipotenusa abbiano rispettivamente lunghezze m − n e 2n −
m. Questa costruzione dimostra l'irrazionalità di
sia razionale deve essere falsa. Da un triangolo rettangolo
isoscele di cui i cateti e l'ipotenusa abbiano rispettivamente lunghezze n
e
m, tramite una classica costruzione con riga e compasso, e' possibile
costruire un triangolo isoscele rettangolo più piccolo tale che i cateti e
l'ipotenusa abbiano rispettivamente lunghezze m − n e 2n −
m. Questa costruzione dimostra l'irrazionalità di 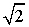 con lo stesso tipo di metodo che fu impiegato dagli antichi
geometri greci.
con lo stesso tipo di metodo che fu impiegato dagli antichi
geometri greci.
Altri numeri irrazionali
Quasi tutti i numeri irrazionali sono trascendenti e tutti i numeri trascendenti sono irrazionali: l'articolo sui numeri trascendenti elenca diversi esempi. er e πr sono irrazionali se r ≠ 0 è razionale; anche eπ è irrazionale.Un altro modo di costruire numeri irrazionali è come numeri algebrici irrazionali, cioè zeri di polinomi a coefficienti interi: iniziamo con un'equazione polinomiale:
p(x) = an xn + an-1 xn−1 + ... + a1 x + a0 = 0
dove i coefficienti ai sono interi. Supponiamo di sapere che esistono numeri reali x tali che p(x) = 0 (per esempio se il polinomio è di grado dispari). Le uniche possibile radici razionali di quest'equazione polinomiale sono della forma r/s dove r è un divisore di a0 ed s è un divisore di an; c'è solo un numero finito di questi candidati che è facile controllare a mano. Se nessuno di loro è una radice di p, allora x deve essere irrazionale. Per esempio, questa tecnica può essere usata per mostrare che x = (21/2 + 1)1/3 è irrazionale: abbiamo (x3 − 1)2 = 2 e quindi x6 − 2x3 − 1 = 0, e quest'ultimo polinomio non ha alcuna radice razionale (gli unici candidati possibili sono ±1).
Poiché i numeri algebrici formano un campo, molti numeri irrazionali possono
essere costruiti combinando numeri algebrici e trascendenti. Per esempio 3π+2, π
+ 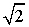 ed
ed 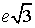 sono irrazionali (nonché trascendenti).
sono irrazionali (nonché trascendenti).
Numeri irrazionali ed espansioni decimali
Spesso si crede erroneamente che i matematici definiscano "numero irrazionale" in termini di espansione decimale, chiamando un numero irrazionale se la sua espansione decimale non si ripete né termina. Nessun matematico utilizza tale definizione, in quanto la scelta della base 10 sarebbe arbitraria e la definizione tipica è più semplice e più motivata. Tuttavia è vero che un numero è nella forma n/m, dove n ed m sono interi, se e solo se la sua espansione decimale si ripete o è finita. Quando l'algoritmo di divisione lunga che tutti hanno imparato nella scuola elementare viene applicato alla divisione di n per m, sono possibili solo m resti. Se 0 appare come resto, l'espansione decimale si conclude. Se 0 non compare, allora l'algoritmo può richiedere al massimo m − 1 passi senza usare ogni resto più di una volta. Dopodiché, un resto deve ricomparire, e quindi l'espanzione decimale si ripete. Al contrario, supponiamo di essere di fronte ad un decimale periodico, ad esempio:Poiché la dimensione del periodo è 3, moltiplichiamo per 103:
e sottraiamo A da entrambi i membri:
Allora
(Il "135" si può trovare rapidamente tramite l'algoritmo di Euclide.)
Numeri di cui non è accertata l'irrazionalità
Non si sa ancora se π + e o π − e sono irrazionali o no. Infatti, non c'è nessuna coppia di interi non nulli m ed n per cui si sappia se mπ + ne è irrazionale o no. Non si sa neanche se 2e, πe, π√2 o la costante di Eulero-Mascheroni sono irrazionali.L'insieme di tutti i numeri irrazionali
L'insieme di tutti i numeri irrazionali non è numerabile (poiché i razionali sono numerabili e i reali non lo sono). L'insieme degli irrazionali algebrici, ossia gli irrazionali non-trascendenti, è numerabile. Usando il valore assoluto per misurare le distanze, i numeri irrazionali diventano uno spazio metrico che non è completo. Tuttavia, questo spazio metrico è omeomorfo allo spazio metrico completo di tutte le sequenze di interi positivi; l'omomorfismo è dato dall'espansione in frazione continua infinita. Questo dimostra che il teorema delle categorie di Baire vale per lo spazio dei numeri irrazionali.IRRIDUCIBILE
In matematica una frazione è irriducibile quando non si può ridurre a forma più semplice.ISOMETRIA
Consideriamo due spazi metrici S ed S' e denotiamo rispettivamente con d e d' le rispettive funzioni distanza. Si definisce isometria di S su S' la trasformazione di S su S' che ad ogni coppia dei punti di S A e B associa rispettivamente i punti A' e B' in modo da mantenere la distanza tra i due: d(A,B) = d'(A',B').Le isometrie sono particolari
trasformazioni lineari: se si parla di spazi vettoriali con prodotto interno e,
in particolare, di spazi euclidei, un'isometria è un isomorfismo (dunque
un'applicazione lineare iniettiva e suriettiva, contemporaneamente monomorfismo
ed endomorfismo) che sussiste tra due spazi della stessa dimensione.
L'isometria, in questo caso, mantiene il prodotto scalare tra i due spazi,
ovvero:
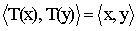 , con T(x), T(y) appartenenti al codominio di T e
x,y appartenenti al dominio di T. Due spazi vettoriali tra i quali esiste
una isometria sono detti spazi isometrici. In particolare, qualunque spazio
euclideo di dimensione n è isometrico allo spazio euclideo canonico di
dimensione n.
, con T(x), T(y) appartenenti al codominio di T e
x,y appartenenti al dominio di T. Due spazi vettoriali tra i quali esiste
una isometria sono detti spazi isometrici. In particolare, qualunque spazio
euclideo di dimensione n è isometrico allo spazio euclideo canonico di
dimensione n.
In uno spazio euclideo le isometrie sono combinazioni di traslazioni e rotazioni. Le traslazioni si possono considerare rotazioni con centro all'infinito.
ISOSCELE
Si definisce triangolo isoscele un triangolo che possiede almeno due lati uguali o equivalentemente un triangolo che possiede almeno due angoli uguali. Infatti vale il seguente teorema:Un triangolo ha due lati uguali se e solo se ha due angoli uguali.
Questo teorema costituisce la quinta proposizione del Libro I degli Elementi
di Euclide ed è noto come Pons asinorum, ponte degli asini.
Particolari triangoli isosceli sono i triangoli equilateri e i triangoli
rettangoli isosceli. Esistono anche triangoli isosceli acutangoli e ottusangoli.
I triangoli isosceli rettangoli sono tutti simili tra di loro, come i triangoli equilateri.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()