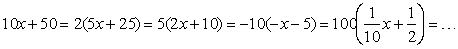Matematica
Dizionario di matematica e geometria con iniziale B 2^ parte
Numeri complessi Numeri Immaginari Numeri Relativi Numeri Naturali Numeri Reali
Aritmetica Geometria Informatica
Geometria Piana e Solida Informatica Media
Geometria piana e Solida
Elementi Fondamentali della Geometria Gli Angoli Il Triangolo Il Cerchio Linee sul Piano Quadrilateri e Poligoni Superficie dei Poligoni Cilindri e Prismi Coni e Piramidi Gli Esaedri La Sfera Geometria Solida Nozioni Generali Solidi di Rotazione
Informatica e Programmazione
Altri Sistemi Operativi Basic Dati e Le Prime Istruzioni Il Trattamento dei Dati Le Funzioni Intrinseche o Predefinite Le Istruzioni di Controllo Linguaggio e Ambiente di Sviluppo Procedure e Funzioni Programmi Dos Suono e Grafica Ricerche Complementari Vettori e Matrici Borland Delphi Caratteristiche dei Linguaggi di Programmazione I Data Base I File Ricerche Complementari I File I Linguaggi di Programmazione I Pacchetti Applicativi Sistemi Operativi Ricerche Complementari Sistemi Operativi Il Multimedia Il Sistema Operativo Dos Ricerche Complementari Il Sistema Operativo Dos Internet e Intranet Introduzione La Programmazione Interfaccia Utente L'Ambiente Microsoft Windows Le Applicazioni Ricerche Complementari Le Applicazioni Le Periferiche del Computer Le Reti di Computer Le Reti Ricerche Complementari Le Strutture di Dati Ricerche Complementari Le Strutture di Dati L'Hardware del PC Ricerche Complementari L'Hardware del Personal Computer Linguaggi Ricerche Complementari Microsoft Visual Basic Periferiche Ricerche Complementari Programmazione la Struttura Condizionale Le Matrici Dall'Algoritmo al Programma I File I Primi Elementi I Vettori Il Controllo degli Errori La Grafica L'Analisi Top Down Programmazione RAD Programmazione Le Matrici Rappresentazione Dati in Memoria Ricerche Complementari Sistemi di Numerazione Storia del Computer Struttura e Funzionamento del Computer Ricerche Complementari Struttura e Funzionamento del Computer
![]()
Formule delle potenze di un binomio (Newton)
Prodotto di una somma per una differenza
Bisettrici di due angoli adiacenti
Bisettrici di due angoli opposti al vertice
![]()
![]()
Dizionario di matematica e geometria iniziale B
BARICENTRO
In geometria, il baricentro (a volte chiamato centroide) di una figura X n-dimensionale in uno spazio euclideo n-dimensionale è l'intersezione di tutti gli iperpiani che dividono X in due parti di misura identica.In modo informale, possiamo dire che è la "media" di tutti i punti di X.
Una figura concava può avere come baricentro un punto che non appartiene alla figura stessa;
ad esempio il baricentro di una falce di luna si trova in un punto del suo asse di simmetria, ma fuori dalla falce stessa.
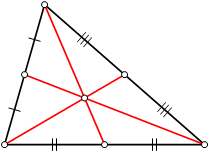
Il baricentro di un triangolo è il punto di intersezione delle sue mediane, cioè dei segmenti che uniscono ciascun vertice con il punto medio del lato opposto.
Per ogni triangolo il baricentro è suo punto interno e si può dimostrare che ciascuna delle tre mediane viene divisa dal baricentro in due parti in rapporto 2:1.
Di regola, il baricentro di un triangolo non è il centro di qualche cerchio notevole collegato al triangolo, inscritto o circoscritto:
questo accade nel caso particolare di un triangolo equilatero.
Passando alle tre dimensioni abbiamo situazioni analoghe per il baricentro dei
tetraedri.
Tale punto si può individuare come punto di incontro di due dei quattro segmenti che uniscono uno dei quattro vertici con il baricentro della faccia triangolare opposta:
i quattro segmenti si incontrano tutti in un punto, il baricentro, il quale divide ciascuno di essi in due parti in rapporto 3:1.
BASE
In matematica, e più precisamente in algebra lineare, un insieme di vettori di uno spazio vettoriale è una base se questi vettori sono indipendenti e generano lo spazio vettoriale.La base è un concetto chiave dell'algebra lineare, essenzialmente per il motivo seguente:
uno spazio vettoriale generalmente non ha una sola base, anzi solitamente ha una infinità di basi molto diverse fra loro;
però queste hanno tutte la stessa cardinalità, sono formate cioè sempre dallo stesso numero di vettori.
Questo numero, che dipende quindi solo da V, è la dimensione di V e ci permette di parlare di spazi di dimensione arbitrariamente alta, superando i limiti della nostra intuizione tridimensionale.
Definizione
Sia V uno spazio vettoriale su un campo K.Un insieme ordinato di vettori (v1, ..., vn) è una base per V se valgono entrambe queste proprietà:
I vettori v1, ..., vn sono linearmente indipendenti;
I vettori v1, ..., vn generano V, cioè V = Span(v1, ..., vn).
Proprietà
L'insieme B = (v1, ..., vn) è una base per V se e solo se ogni elemento v di V si può scrivere in un modo solo come combinazione lineare dei vettori v1, ..., vn.Due basi B e B' di V hanno sempre la stessa cardinalità, detta dimensione di V.
Tale cardinalità è pari al massimo numero di vettori indipendenti in V e al minimo numero di vettori necessari per generare V.
Le due proprietà seguenti mostrano che, se conosciamo già la dimensione dello spazio, per verificare che un insieme del numero giusto di elementi sia una base basta dimostrare una sola delle due proprietà necessarie:
Un insieme B di n vettori in uno spazio V di dimensione n è una base se e solo se sono indipendenti.
Un insieme B di n vettori in uno spazio V di dimensione n è una base se e solo se generano V.
![]()
![]()
Esempi
I vettori (1,0) e (0,1) sono una base di R2, perché sono indipendenti e generano R2 (infatti ogni altro (a, b) si scrive come (a, b) = a(1,0) + b(0,1)).In dimensione arbitraria, una base dello spazio vettoriale Rn è data dai vettori
e1 = (1, 0, 0, ..., 0), e2 = (0, 1, 0, ...,0), ..., en = (0, ..., 0, 1).
Questa base si chiama base canonica di Rn.
La base canonica di Cn, cioè lo spazio vettoriale delle n-uple di numeri complessi, è sempre
e1 = (1, 0, 0, ..., 0), e2 = (0, 1, 0, ...,0), ..., en = (0, ..., 0, 1).
È facile infatti scrivere un qualsiasi vettore di Cn come combinazione di questi.
Ad esempio il vettore (i, 0, 0) si scrive come
i * (1 , 0 , 0) = (i , 0 , 0)
I vettori (3,1) e (-1,2) formano una base di R2, diversa da quella canonica:
visto che sono 2 vettori in uno spazio che sappiamo già avere dimensione 2, grazie alla proprietà descritta sopra per dimostrare questo fatto ci basta notare che sono indipendenti.
In geometria la parola base prende primariamente significato dal greco baínein, che vuol dire "appoggiarsi su", e indica che una figura è costruita su certi elementi o a partire da essi.
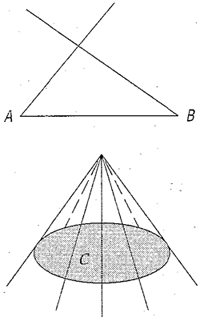
Per esempio supponiamo di dover costruire, a partire da un segmento AB, un triangolo con certe proprietà, oppure, a partire da un cerchio C, un cono soddisfacente a certe condizioni:
la base di un triangolo o quella di un cono avrebbero funzione analoga, pur essendo di natura diversa.
Il significato di base si riallaccia a volte a quello corrente di "parte
inferiore" di un oggetto;
in esso la parte più alta si chiama a volte vertice e l'altezza dell'oggetto è la distanza fra le due.
BINARIA, NUMERAZIONE
Sistema di numerazione a base due, in cui bastano due cifre 1 e 0, per scrivere tutti i numeri.Ecco una tabella che confronta le rappresentazioni binarie, esadecimali e decimali di alcuni numeri
|
Binario Esadecimale
Decimale |
|
0000 =
0 =
0 |
|
0001 =
1 =
1 |
|
0010 =
2 =
2 |
|
0011 =
3 =
3 |
|
0100 =
4 =
4 |
|
0101 =
5 =
5 |
|
0110 =
6 =
6 |
|
0111 =
7 =
7 |
|
1000 =
8 =
8 |
|
1001 =
9 =
9 |
|
1010 =
A =
10 |
|
1011 =
B =
11 |
|
1100 =
C =
12 |
|
1101 =
D =
13 |
|
1110 =
E =
14 |
|
1111 =
F =
15 |
È usata in informatica per la rappresentazione interna dei numeri, grazie alla semplicità di realizzare fisicamente un elemento con due stati anziché un numero superiore, ma anche per la corrispondenza con i valori logici vero e falso.
È considerato tra le più grandi invenzioni del matematico tedesco G. Leibniz;
purtroppo però essa cadde nel vuoto e solo nel 1847 verrà riscoperta, grazie al matematico inglese G. Boole, che aprirà l'orizzonte alle grandi scuole di logica matematica del '900 e soprattutto alla nascita del calcolatore elettronico.
La formula per convertire un numero da binario a decimale (dove con d si indica la cifra di posizione n all'interno del numero, partendo da 0) è
d(n - 1)2(n - 1) + ... + d020 = N
Ad esempio:
10012=1*23+0*22+0*21+1*20=910
![]()
Guadagnare navigando! Acquisti prodotti e servizi.
Guadagnare acquistando online.
![]()
BINOMIO
Un binomio è un'espressione algebrica nella quale figurano due termini, due monomi non simili, collegati da un segno di addizione o di sottrazione.Per esempio, sono binomi
a+b, a-bc,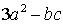 ,
2x-+ 3.
,
2x-+ 3.
I binomi- sono dunque i polinomi del tipo più semplice dopo i monomi (che sono anch'essi dei polinomi particolari).
I binomi intervengono in molte identità notevoli utili per i calcoli algebrici.
Calcoli con i binomi
Formule delle potenze di-un-binomio (Newton)
Un binomio può essere moltiplicato per se stesso indefinitamente;si ottengono così le sue potenze successive, delle quali diamo qui qualche esempio:

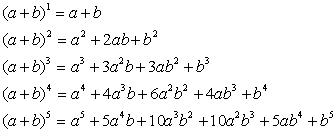
La formula che dà la potenza n-esima, che qui non scriviamo;
si chiama anche "binomio di Newton".
I coefficienti dei polinomi potenza si possono scrivere in uno schema, che prende il nome di "triangolo di Tartaglia" o "di Pascal":

Si osserva che il primo e l'ultimo coefficiente sono 1 e ogni numero è la somma
dei due numeri più vicini della fila superiore.
Questa regola permette di trovare-subito i coefficienti delle potenze successive.
Prodotto di una somma per una differenza
Calcoliamo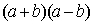 ;
applicando la proprietà distributiva e successivamente la commutativa:
;
applicando la proprietà distributiva e successivamente la commutativa:
![]()
Fattorizzazione di binomi
Quando si deve fattorizzare un'espressione algebrica, un binomio è la più piccola "unità" che si può trovare. In effetti, un binomio nel quale compaiono coefficienti numerici si può scrivere in infiniti modi:
![]()
La scelta fra tutte queste può essere suggerita dal contesto; di regola, la
più semplice (quando i coefficienti sono interi) è quella che mette in evidenza
un binomio i cui coefficienti sono
primi fra loro. In questo caso sarebbe  .
.
BIQUADRATICO
Un'equazione biquadratica è un'equazione di quarto grado nella quale l'incognita figura solo alla seconda e alla quarta potenza, cioè come "quadrato" e "quadrato di quadrato"; essa è dunque della forma:
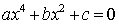
Sostituendo X a 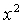 ,
la sua risoluzione si riconduce a quella di un'equazione di secondo grado.
,
la sua risoluzione si riconduce a quella di un'equazione di secondo grado.
BISETTRICE
La bisettrice di un angolo è quella semiretta che parte dal vertice dell'angolo e lo divide in due angoli esattamente congruenti. La bisettrice di un angolo è asse di simmetria dell'angolo.Proprietà delle bisettrici
Dato un angolo, i punti sulla bisettrice hanno uguale distanza dalle due semirette che lo formano.Bisettrici di due angoli adiacenti
Dati due angoli adiacenti, e quindi supplementari si dimostra facilmente che le bisettrici:dei due angoli sono perpendicolari, poiché l'angolo da esse individuato è formato dalla metà degli angoli dati.
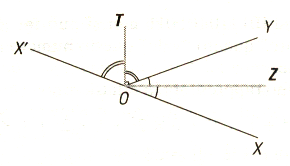
Le bisettrici di due angoli adiacenti sono perpendicolari.
Bisettrici di due angoli opposti al vertice
Se due angoli sono opposti al vertice; le loro bisettrici sono una il prolungamento dell'altra. Esse sono, infatti, entrambe perpendicolari alla semiretta OT, dunque il loro angolo è piatto.
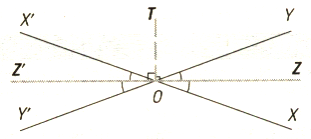
Bisettrici di un triangolo
Il concetto di bisettrice si applica in particolare al triangolo, dove indica il segmento di bisettrice che divide un angolo in due parti uguali e si ferma sul lato opposto. Quindi, se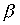 è l'angolo più piccolo ricavato con la bisettrice e
è l'angolo più piccolo ricavato con la bisettrice e
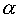 l'angolo considerato all'inizio, possiamo scrivere:
l'angolo considerato all'inizio, possiamo scrivere:
![]() o se si preferisce
o se si preferisce
![]()
In un triangolo, le tre bisettrici si incontrano in un punto, chiamato incentro. Esso è uno dei punti notevoli di un triangolo e non può mai cadere all'esterno del triangolo stesso né sul suo perimetro. Inoltre, per la proprietà di cui sopra, si ha che l'incentro è il punto del triangolo equidistante dai tre lati. Dall'incentro si può poi costruire il cerchio inscritto del dato triangolo. Considerando un triangolo ABC e la bisettrice dell'angolo BÂC che incontra il lato BC in M sussiste la seguente proporzione:
AB:AC = BM:MC,
che deriva direttamente dal teorema di Talete.
![]()
![]()
Enciclopedia termini lemmi con iniziale a b c d e f g h i j k l m n o p q r s t u v w x y z
Storia Antica dizionario lemmi a b c d e f g h i j k l m n o p q r s t u v w x y z
Dizionario di Storia Moderna e Contemporanea a b c d e f g h i j k l m n o p q r s t u v w y z
Lemmi Storia Antica Lemmi Storia Moderna e Contemporanea
Dizionario Egizio Dizionario di storia antica e medievale Prima Seconda Terza Parte
Storia Antica e Medievale Storia Moderna e Contemporanea
Dizionario di matematica iniziale: a b c d e f g i k l m n o p q r s t u v z
Dizionario faunistico df1 df2 df3 df4 df5 df6 df7 df8 df9
Dizionario di botanica a b c d e f g h i l m n o p q r s t u v z
![]()